De baan is de cirkel met middelpunt en straal . Hij wordt in tegenwijzerrichting doorlopen in seconden, dus de snelheid is .
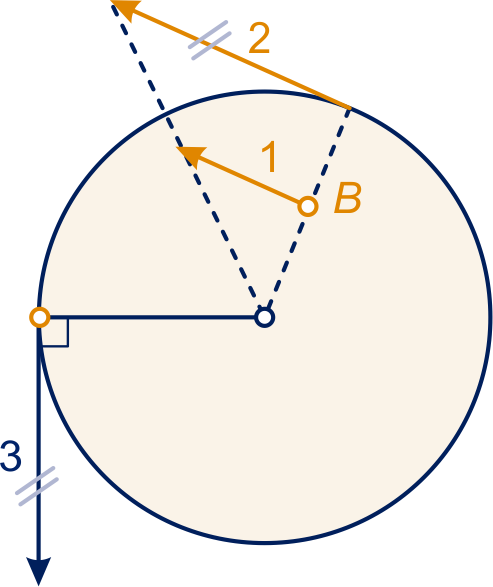
De pijlen 1 en 2 zijn evenwijdig; de pijlen 2 en 3 zijn even lang en pijl 3 staat loodrecht op lijn en is net als pijl 1 linksom gericht.
De baan is de cirkel met middelpunt en straal . Hij wordt in tegenwijzerrichting doorlopen in seconden, dus de snelheid is .
Het verschil is dat de baan in wijzerrichting doorlopen wordt.
De baan is een cirkel met middelpunt en straal . De baan wordt in wijzerrichting doorlopen in seconden.
Bijvoorbeeld tussen de tijdstippen en wordt afstand afgelegd en tussen de tijdstippen en wordt afstand afgelegd.
Er wordt een afstand van afgelegd, dat zijn rondjes, dus keer (inclusief op het moment van de start).
De afgelegde afstand is ;
De snelheid is ().
De grootte van de vector uit d is:
.
Je kunt het ook zo doen:
;
heeft lengte , dus de gevraagde lengte is .
De -component van de snelheidsvector is: .
de -component van de snelheidsvector is:
.
.
Het kan ook met minder gereken: in a hebben we gezien dat: . Differentiëren naar geeft volgens de kettingregel:
.
;
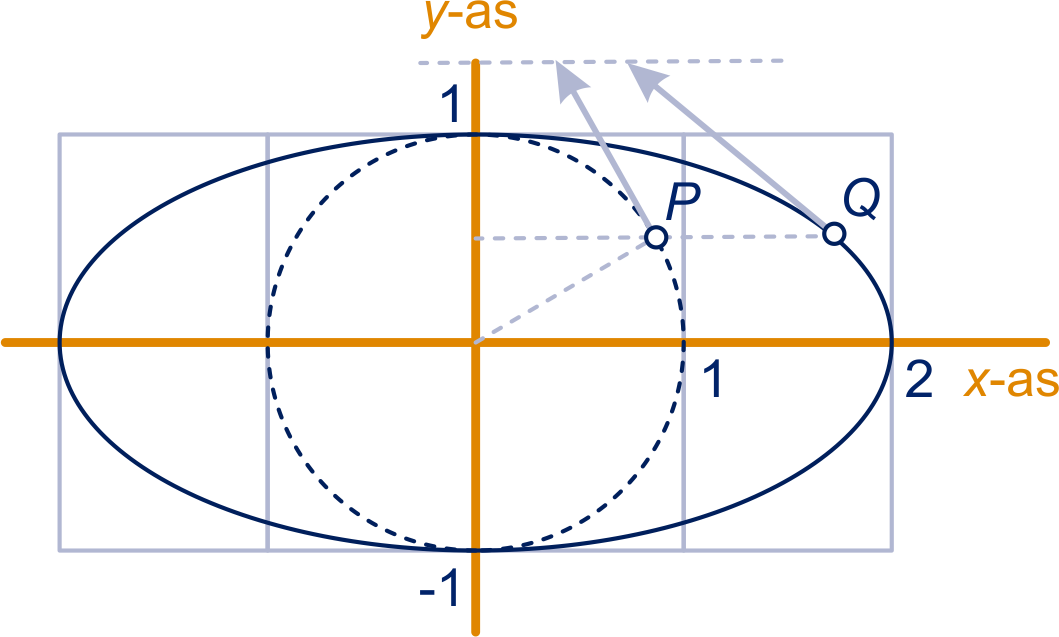
Teken de snelheidsvector in en vermenigvuldig die horizontaal met , immers de snelheid in de -richting wordt keer zo groot en blijft in de -richting hetzelfde.
In de snijpunten met de -as, dan wordt er maximaal 'geprofiteerd' van de horizontale vermenigvuldiging.
De grootte van de snelheidsvector is
.
is maximaal als maximaal is, dat is als , dus in de snijpunten met de -as.
en
Snijpunten met de -as:
, de snijpunten zijn dus:
.
De snijpunten met de -as zijn: .
-
Horizontaal met , verticaal met .
en
en , dus:
en wijst in de richting van de straal en staat loodrecht op de straal, want deze vector heeft inproduct met .
Zie figuur op de volgende bladzijde.
Eerste manier:
.
Tweede manier, zie figuur op de volgende bladzijde: de tangentiële component heeft lengte en de radiële heeft lengte
, dus de somvector heeft lengte .
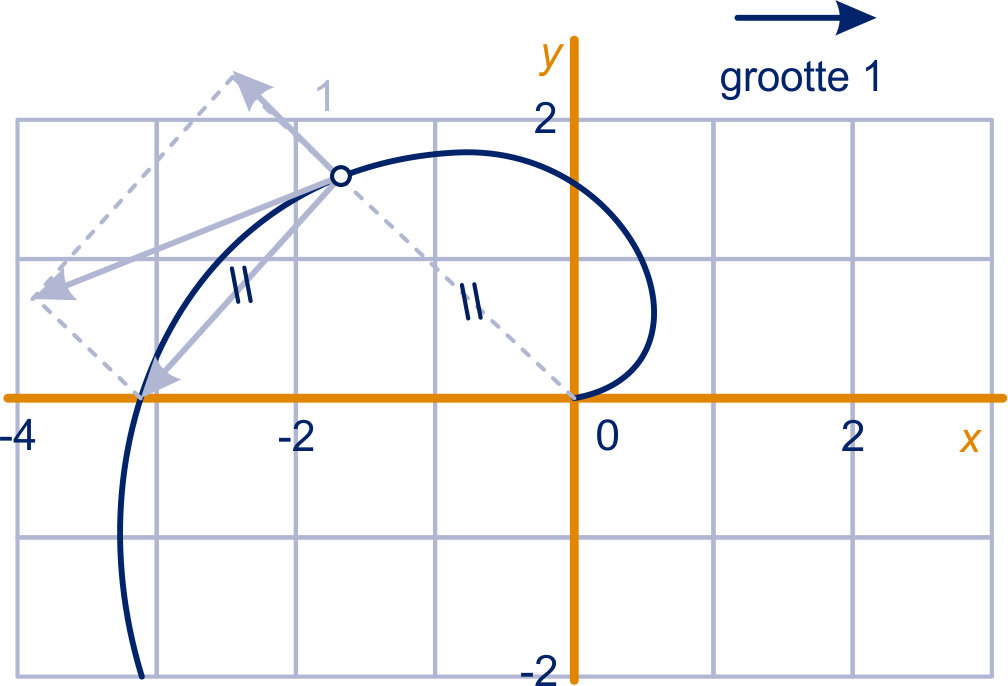
De versnellingsvector is tegengesteld aan .
De versnellingsvector heeft grootte en de snelheidsvector heeft grootte
.
.
, valversnelling.
De versnellingsvector is: .
De grootte van die vector is: . Deze is minimaal als
, dus in .
