Natuurbeschermers willen een monumentale boom op kaart vastleggen. Met een GPS instrument is dat tegenwoordig niet moeilijk. Toen die er nog niet waren, gebeurde dat met hoekmeting. In het veld kun je hoeken meten met een theodoliet.
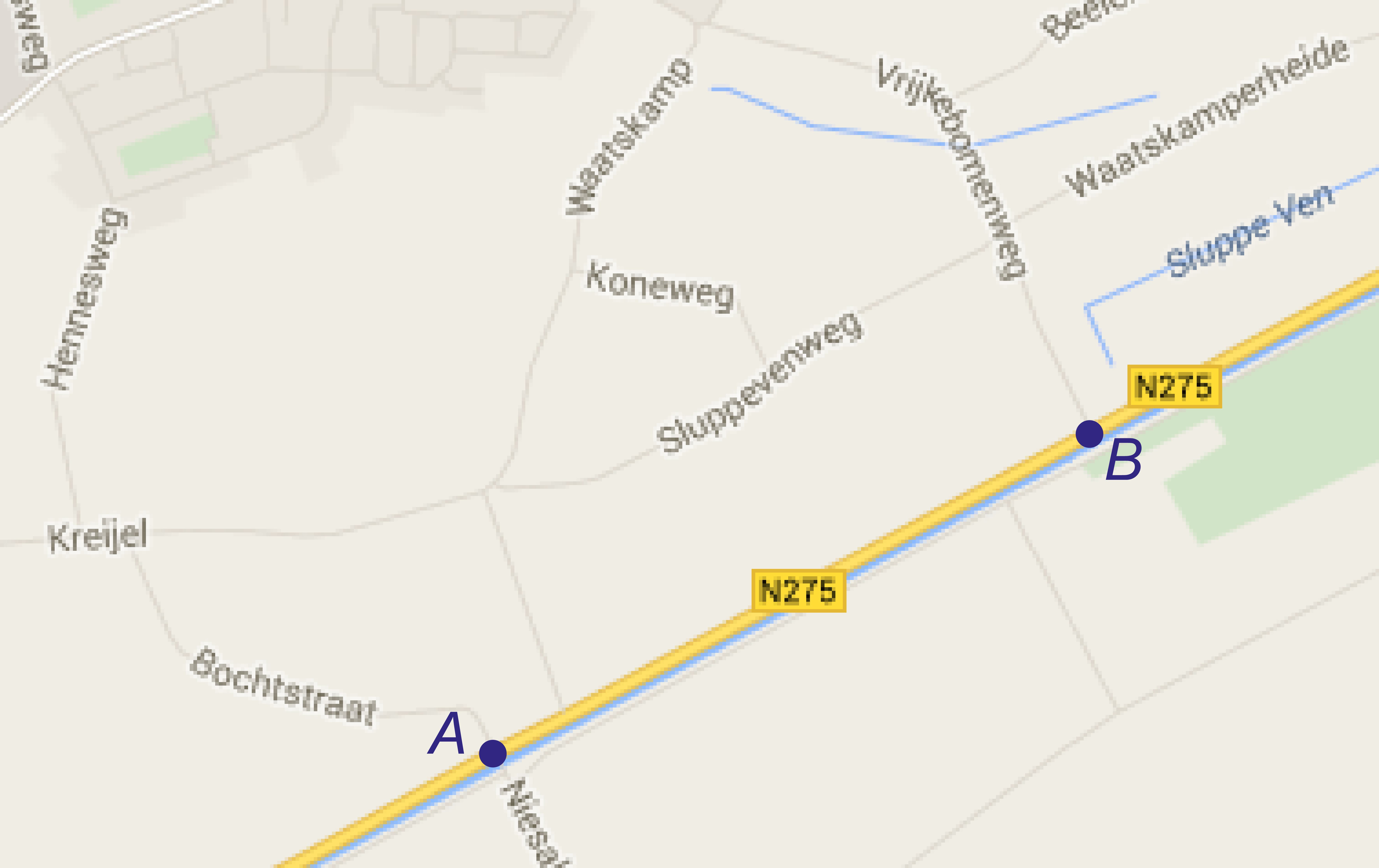
Het punt waar de Bochtstraat op de N275 uitkomt, noemen we en het punt waar de Vrijkebomenweg op de N275 uitkomt, .
De boom staat ten noorden van de N275.
De plaats waar de boom staat noemen we . In meet je hoek , die is . In meet je hoek , die is .
Teken het punt op het kaartje op het werkblad.
De afstand van tot is meter.
Teken driehoek op schaal. Neem cm.
Meet in je driehoek hoe ver de boom van af staat. Schrijf je berekening op.
Een driehoek ligt vast als je twee hoeken en een zijde van de driehoek kent. Je kunt de driehoek tekenen en de zijden die je nog niet kent opmeten. Je kunt ze ook berekenen, dat gaat met de sinusregel. Daarover gaat deze paragraaf.

De opening aan de voorkant van een luciferdoosje is een rechthoek van cm hoog en cm breed. De lege huls van het doosje wordt langzaam platgedrukt. In alle tussenstadia is de opening een parallellogram met zijden van en cm. Zie figuur 1.

De oppervlakte van de opening wordt steeds kleiner. In figuur 2 zie je de voorkant. De scherpe hoek tussen de zijden is .
Bereken de hoogte van het parallellogram exact.
Het parallellogram kun je zo in tweeën knippen dat je er een rechthoek van kunt leggen.
Laat met een schetsje zien hoe dat gaat.
Bereken de oppervlakte van het parallellogram exact.
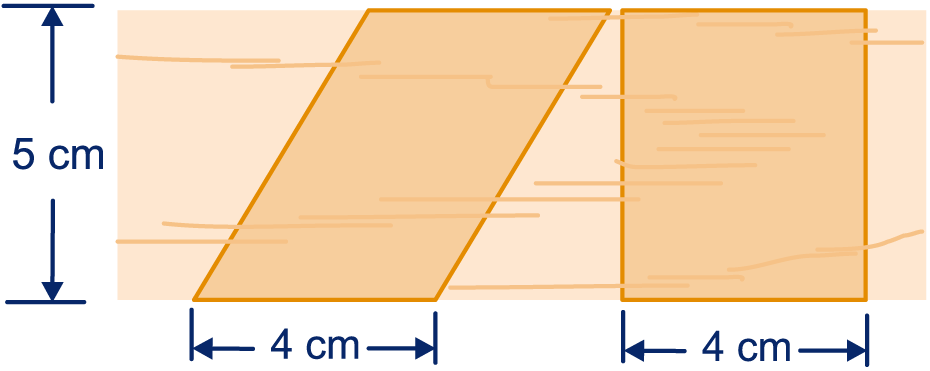
Uit een plank van cm breed wordt een parallellogram gezaagd. Dat is onderaan (en dus ook bovenaan) cm breed.
Laat met een schets zien dat je het parallellogram met één keer knippen tot een rechthoek van bij cm kunt leggen.
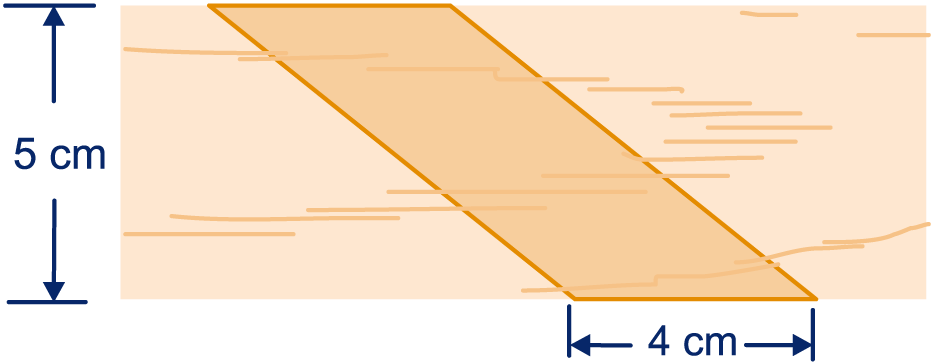
Ook van het parallellogram in figuur 2 kun je een rechthoek van bij cm maken. Je moet wel twee keer knippen.
Laat zien hoe.
Wat is de oppervlakte van het parallellogram in figuur 2?
Het parallellogram in figuur 1 heeft zijden van en . Eén van de hoeken tussen de zijden is .
Bereken de exacte hoogte van het parallellogram en de oppervlakte.
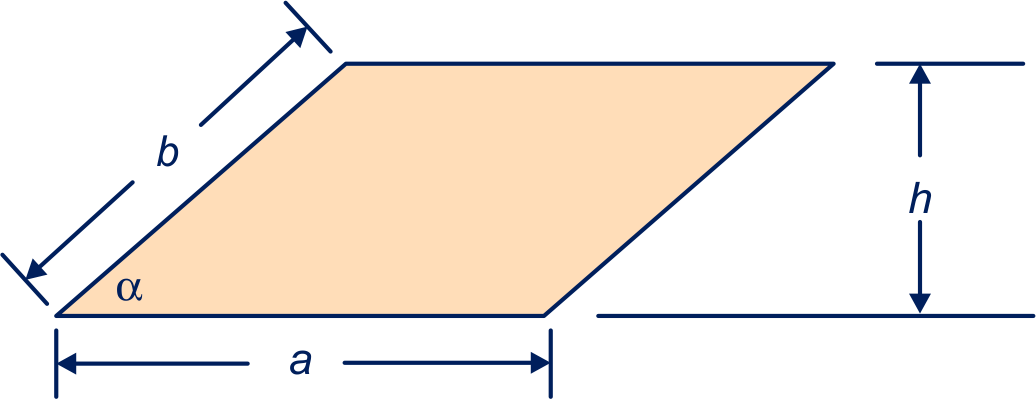
Bij het parallellogram in figuur 2 zijn de zijden en en de (scherpe) hoek tussen de zijden is α.
Druk uit in α en .
Laat zien dat de oppervlakte van het parallellogram in figuur 2 gelijk is aan sin(α).
De twee stompe hoeken van het parallellogram noemen we .
Waarom is de oppervlakte van het parallellogram ook gelijk aan sin(β)?
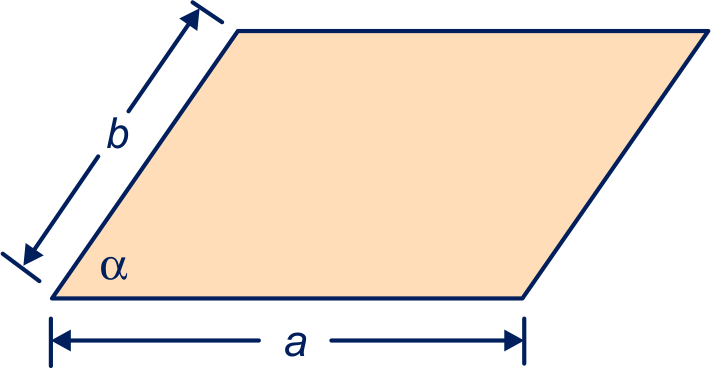
De zijden van een parallellogram zijn en . Een van de hoeken van het parallellogram is α.
Dan is de oppervlakte van het parallellogram: sin(α).
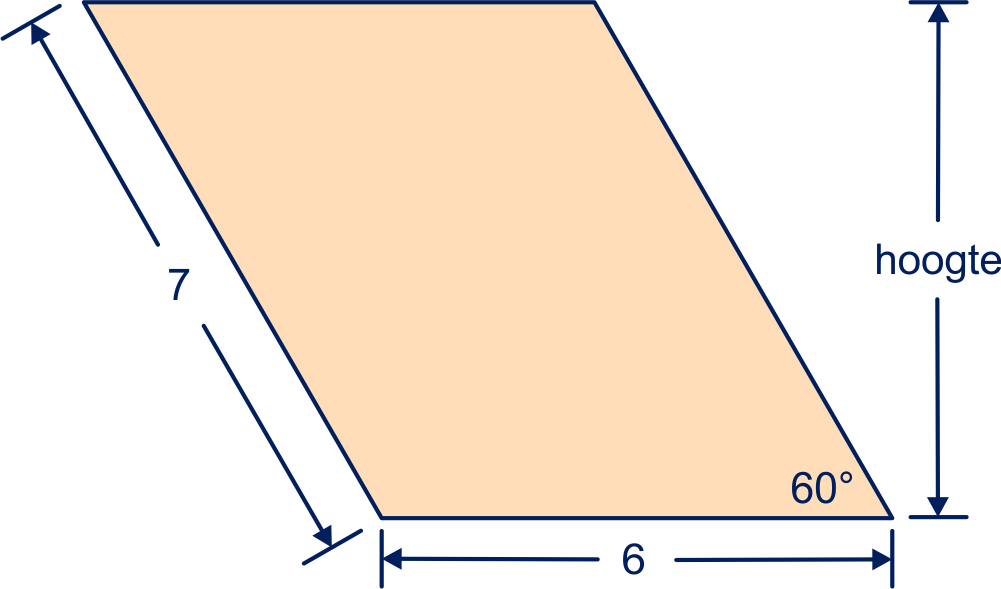
In figuur 1 hieronder staat een parallellogram met zijden en . Eén van de hoeken is .
Bereken de oppervlakte van het parallellogram in figuur 1 exact.
De oppervlakte van het parallellogram is: .

figuur 1
|
figuur 2
|
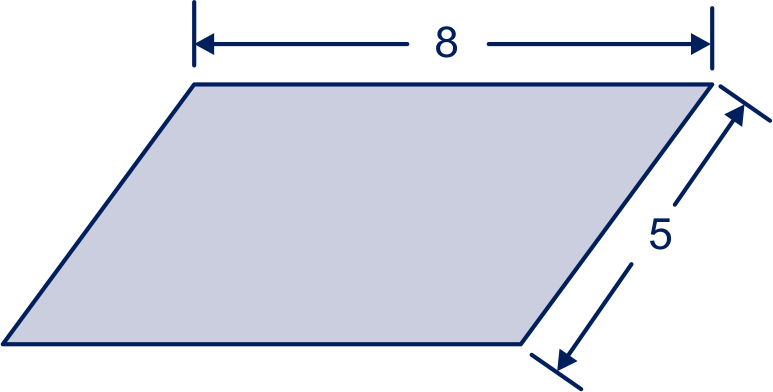
Het parallellogram in figuur 2 heeft zijden en .
De oppervlakte van het parallellogram is .
Bereken de hoeken van het parallellogram in één decimaal.
Noem één van de scherpe hoeken van het parallellogram .
Dan geldt: , dus
, dus
.
Dus twee hoeken zijn en twee hoeken zijn
.

Bereken de oppervlakte van het parallellogram hiernaast in twee decimalen.
Van een parallellogram zijn de zijden en lang. De hoeken van het parallellogram zijn en graden.
Bereken de exacte oppervlakte van het parallellogram.
Van een parallellogram zijn de zijden en . De oppervlakte van het parallellogram is .
Bereken de hoeken van het parallellogram in graden nauwkeurig.
De getekende sterren zijn opgebouwd uit dezelfde ruiten met zijde .
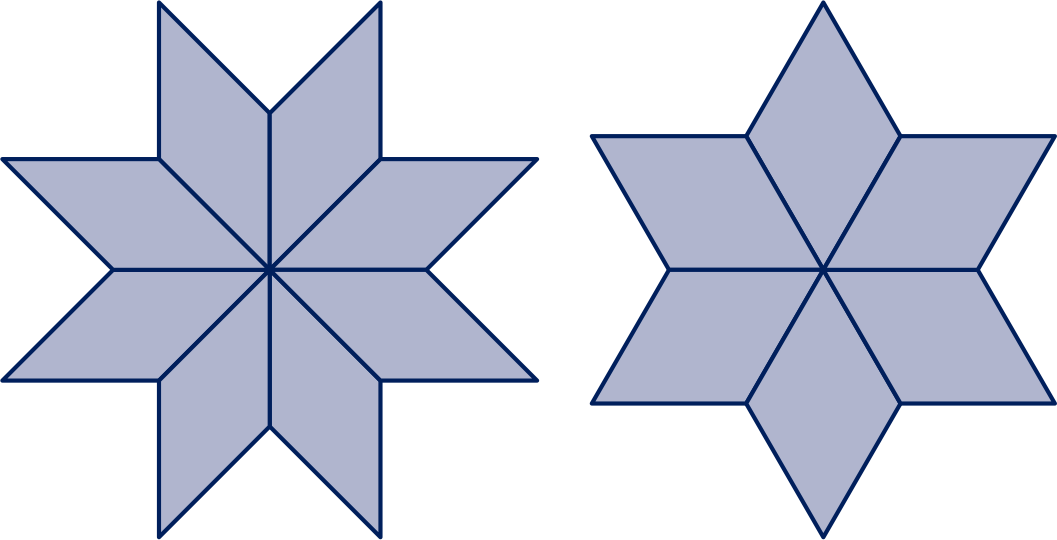
Bereken van elke ster de oppervlakte. Geef een exact antwoord en een benadering in twee decimalen.
Afspraak
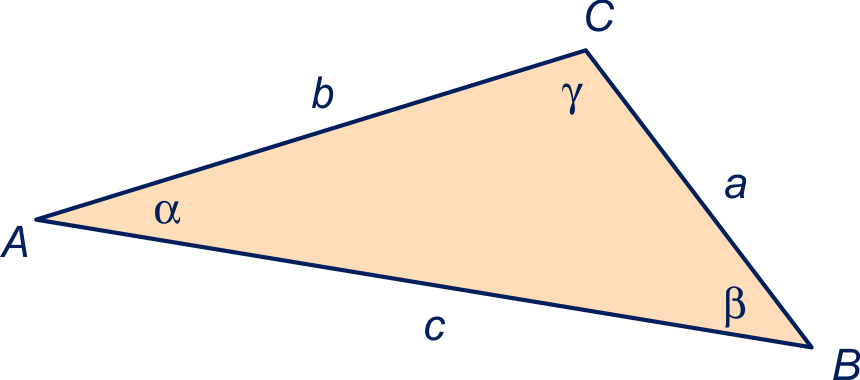
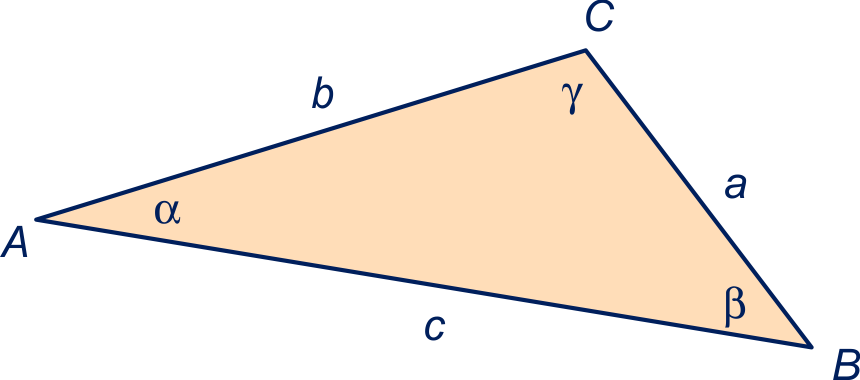
In driehoek noemen we
|
de grootte |
van hoek |
α |
|
|
van hoek |
β |
|
|
van hoek |
γ |
|
de lengte |
van zijde |
|
|
|
van zijde |
|
|
|
van zijde |
|
Merk op dat:
de zijde met lengte tegenover hoek
ligt,
de zijde met lengte
tegenover hoek en
de zijde met lengte tegenover hoek .
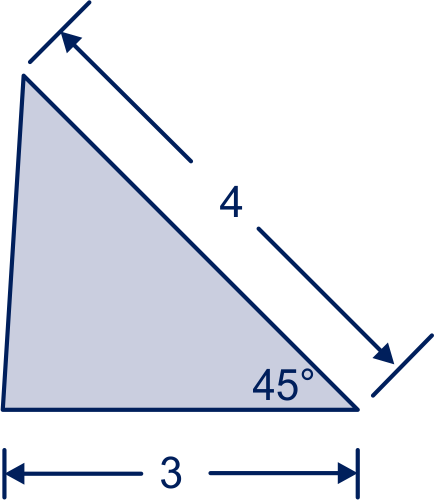
Een driehoek heeft zijden van en . De hoek tussen de zijden is . Met nog zo'n driehoek kun je een parallellogram maken zó dat een van de hoeken van het parallellogram is.
Laat in een schets zien hoe.
Bereken de oppervlakte van het parallellogram exact.
Wat is de oppervlakte van de driehoek dus?
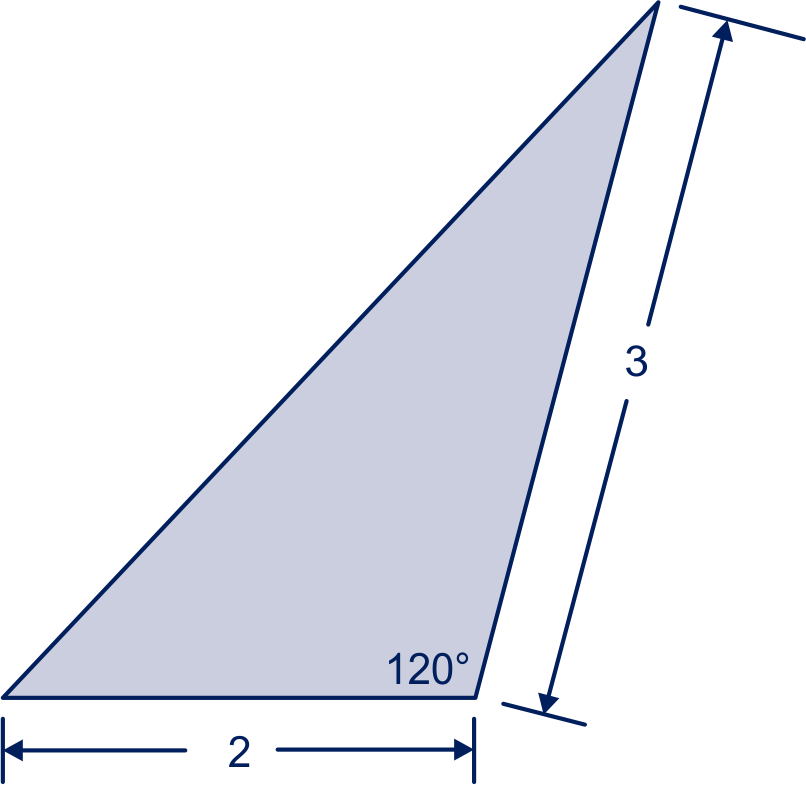
Met twee dezelfde driehoeken als hiernaast kun je een parallellogram maken met zijden en waarvan één van de hoeken is.
Laat zien hoe.
Bereken de oppervlakte van de driehoek hiernaast exact.
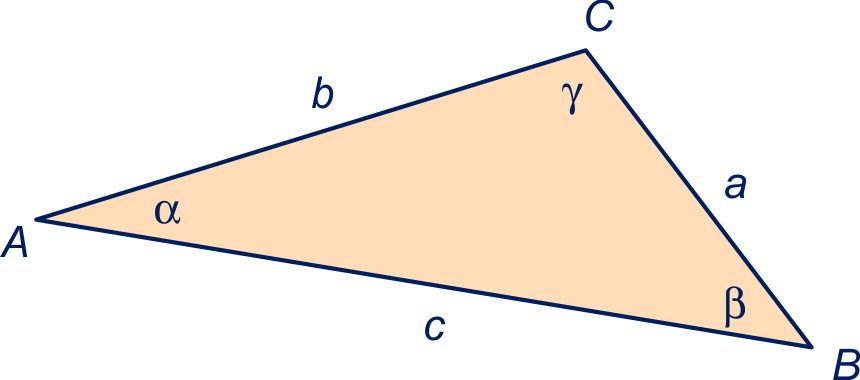
| De oppervlakte van driehoek | sin(γ) |
| sin(α) | |
| sin(β) |
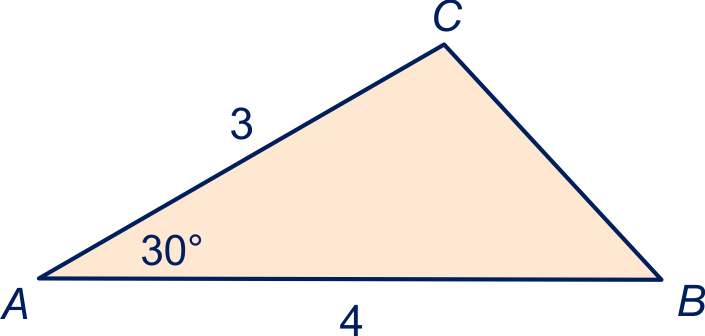
Zie figuur 1 hieronder.
Bereken de oppervlakte van driehoek exact.
De oppervlakte driehoek is .
figuur 1
|
figuur 2
|
Zie figuur 2.
Het latje van lengte
zit scharnierend aan latje van
lengte vast.
Tussen en is een elastiekje gespannen.
Als je hoek groter maakt, wordt de oppervlakte van
driehoek eerst groter en als de hoek stomp wordt, weer kleiner.
Bereken hoek in graden nauwkeurig als de oppervlakte van driehoek gelijk is aan . (Er zijn dus twee oplossingen.)
Er geldt: , dus
.
, dus als
hoek scherp is, dan
en als hoek
stomp is, dan
.
Van driehoek is gegeven: hoek is , en .
Bereken de oppervlakte van driehoek exact.
Van driehoek is de oppervlakte . Verder: en .
Bereken hoek in graden nauwkeurig.
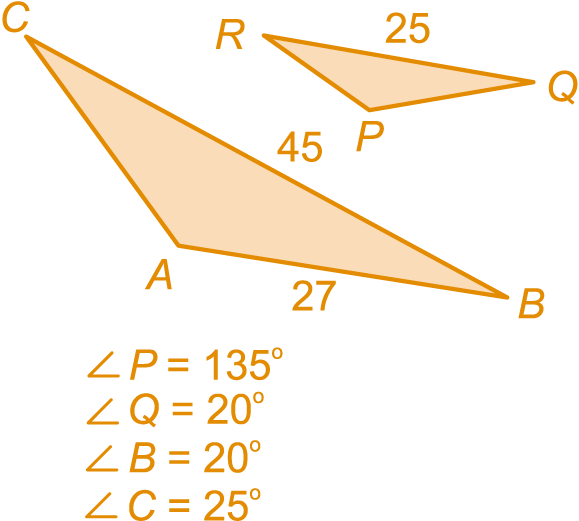
In opgave 8 heb je gezien dat de twee driehoeken in het plaatje rechts gelijkvormig zijn, dat de vergrotingsfactor van groot naar klein is en dat .
Bereken de oppervlakte van de grote en de kleine driehoek in twee decimalen.
Nu je de oppervlakte van de grote driehoek kent, kun je ook de derde zijde van driehoek
uitrekenen.
Er geldt:
oppervlakte driehoek .
Ga dat na en bereken hiermee in één decimaal.
Van de scherphoekige driehoek is de oppervlakte . Zijde en zijde .
Bereken hoek exact.
Bereken de lengte van zijde exact.
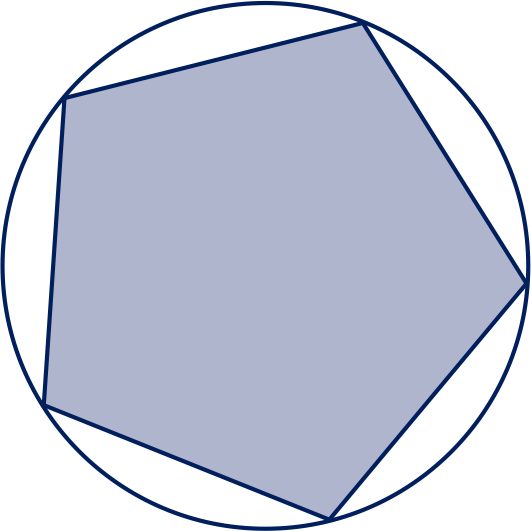
De hoekpunten van een regelmatige vijfhoek met oppervlakte liggen op een cirkel.
Bereken de straal van die cirkel in twee decimalen.
Uit de regel voor het berekenen van de oppervlakte van een driehoek hierboven volgt: sin(γ) sin(α) sin(β).
Vermenigvuldig de regel hierboven met en deel daarna door .
Dan krijg je het volgende.
Sinusregel
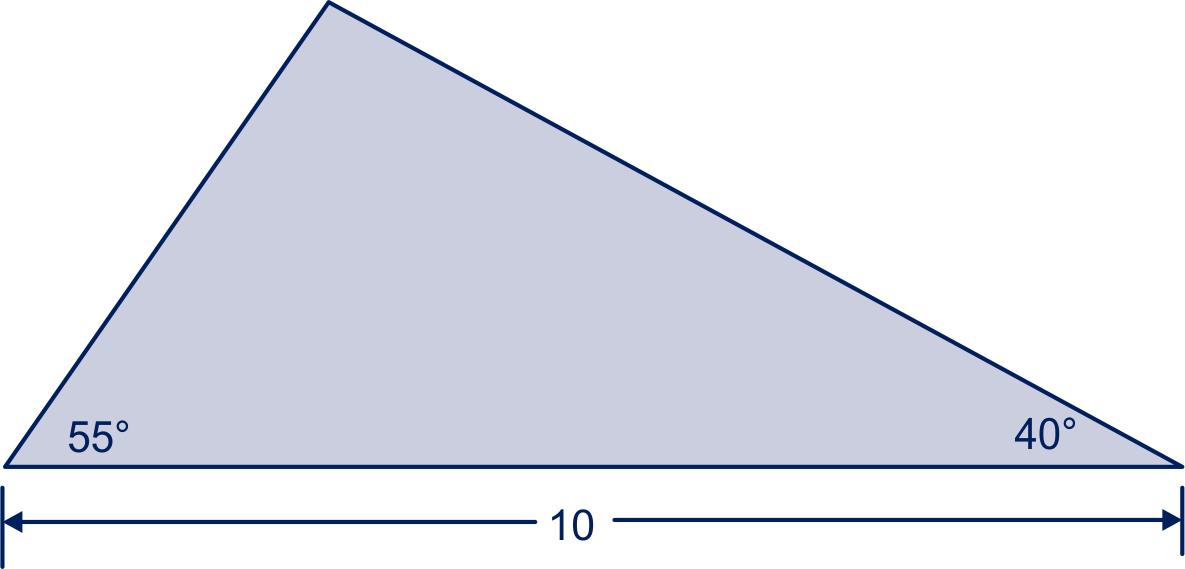
Zie figuur 1 hieronder.
Bereken in twee decimalen.
Er geldt: , dus .

figuur 1
|
figuur 2
|
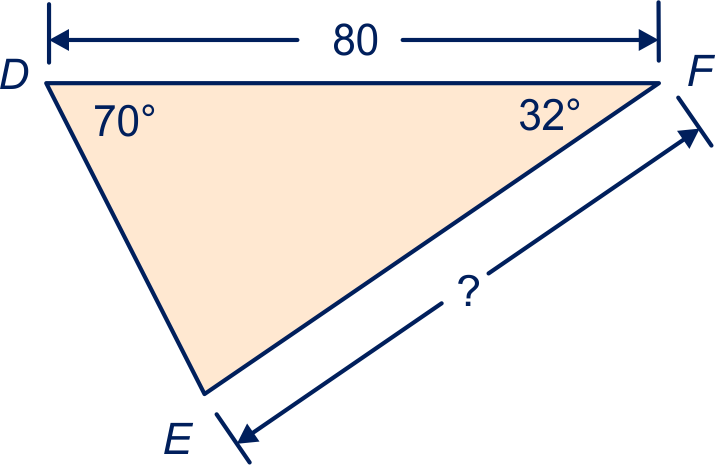
Zie figuur 2.
Bereken de lengte van de zijden van de driehoek tegenover de hoeken van en in twee decimalen nauwkeurig.
We noemen de hoekpunten van de driehoek , en , met linksonder en rechtsonder.
Dan geldt volgens de sinusregel:
Dus:
en .
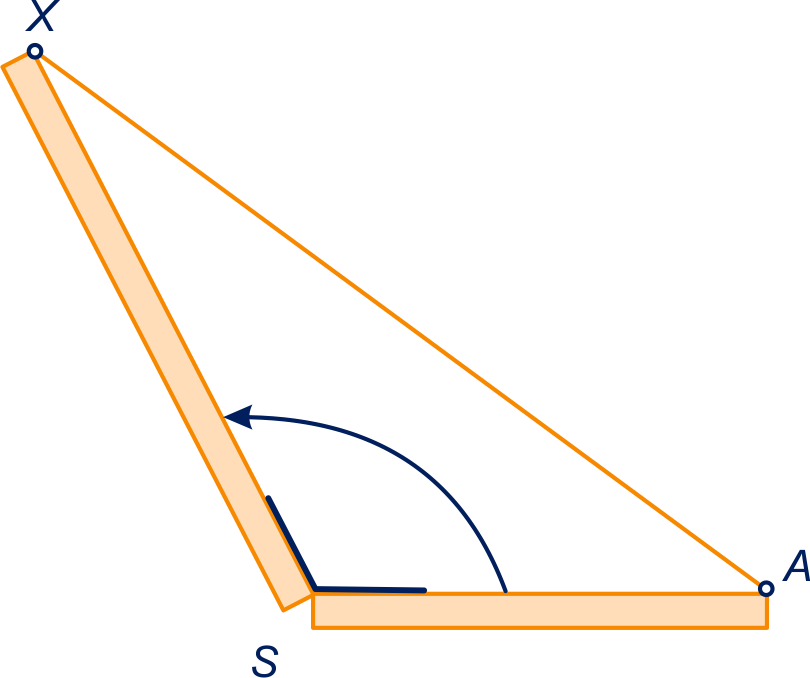
Bekijk nog eens het antwoord van opgave 26, zie figuur.
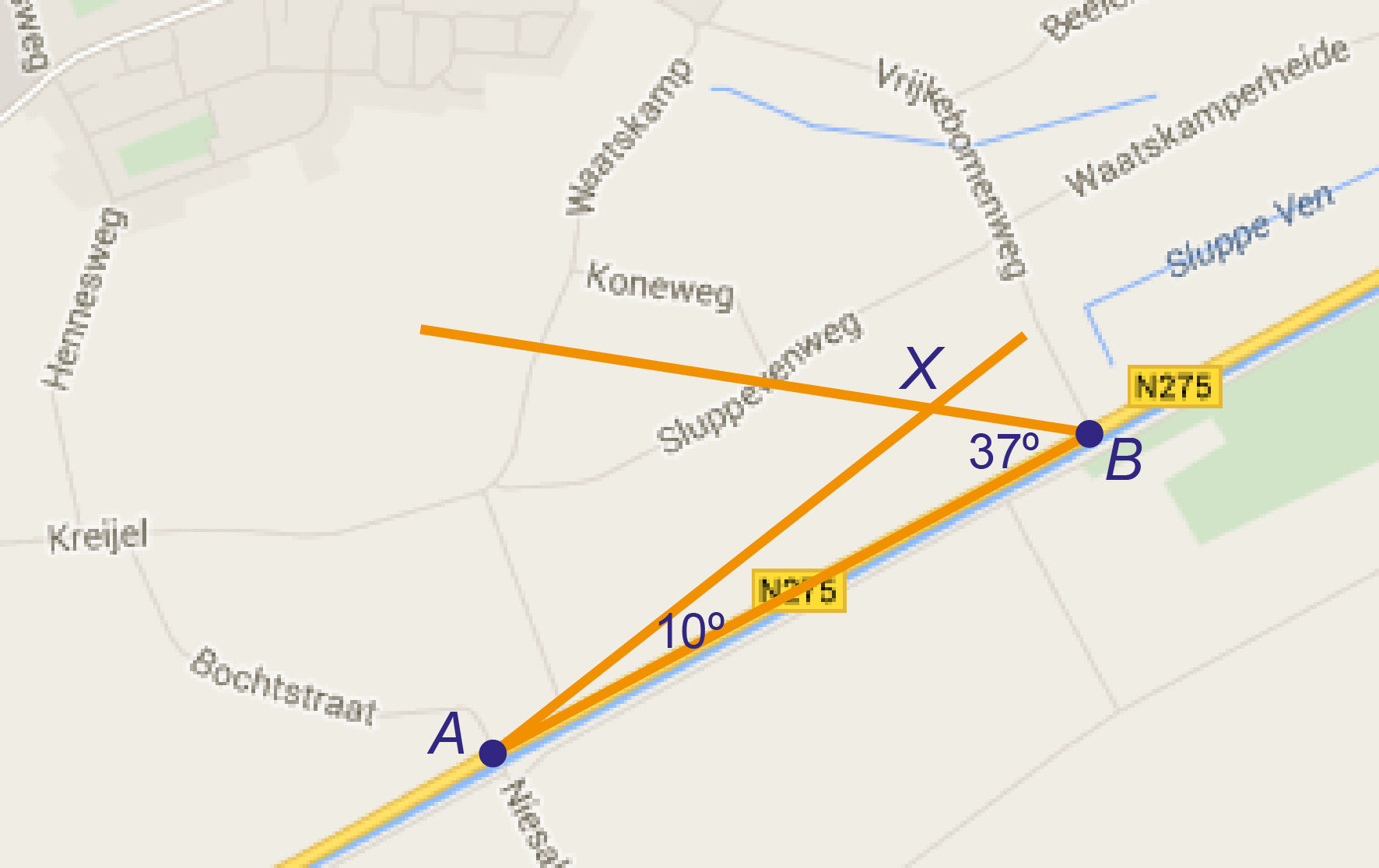
Gegeven is: meter, en .
Bereken de afstand van tot in meter nauwkeurig.
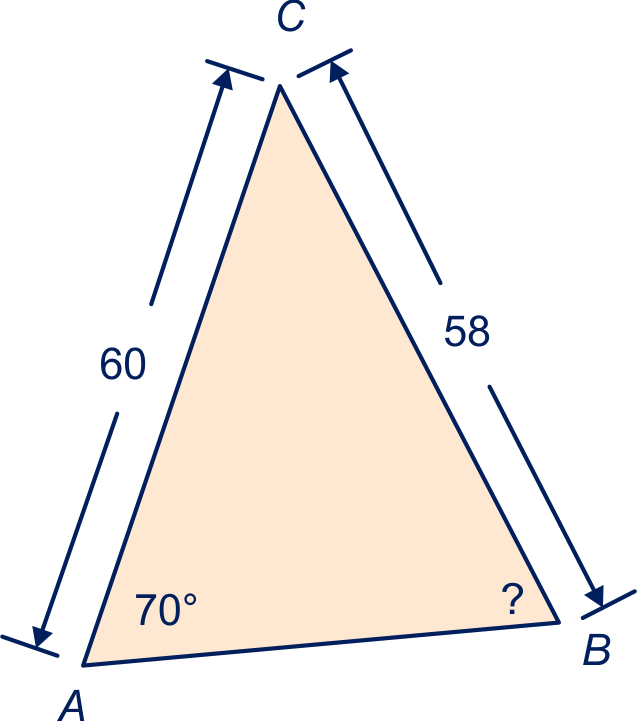
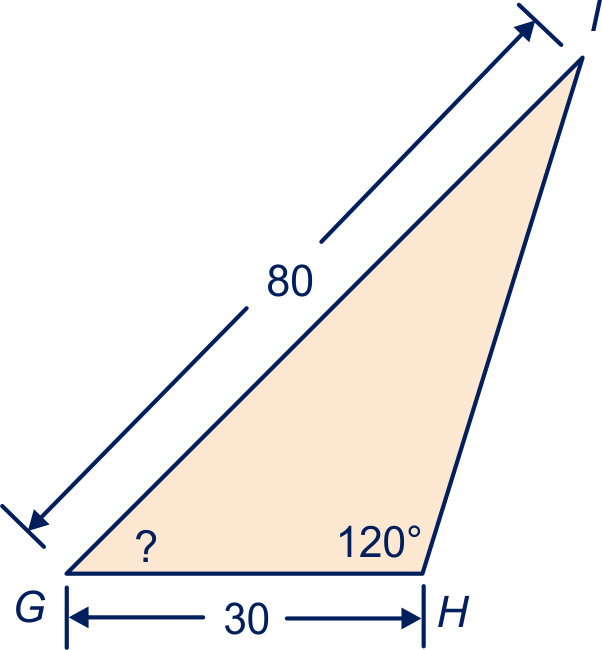
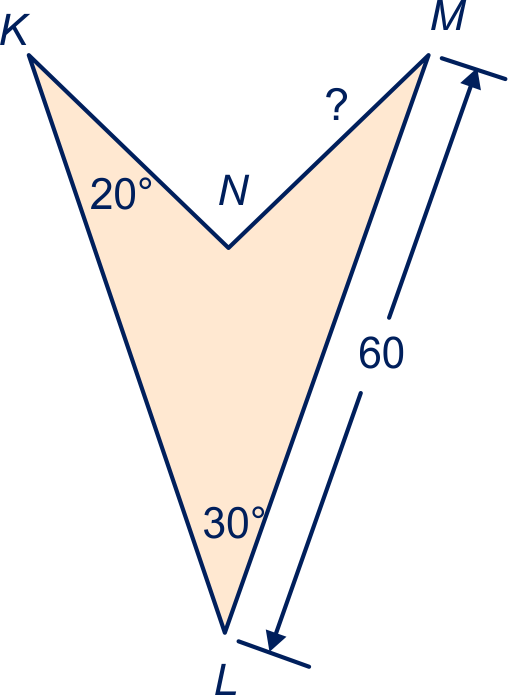
Bereken in de volgende vijf figuren de zijde of hoek waar het vraagteken bij staat.
Vierhoek is een symmetrische pijlpuntvlieger.
Geef je antwoorden in één decimaal nauwkeurig.
|
|
|
|

|
Bekijk nog eens driehoek in de vorige opgave.
Je vindt . De rekenmachine geeft een scherpe hoek van ongeveer bij een hoek waarvan de sinus is. In dit geval moet je een stompe hoek hebben, dus , want .
Een hoek ligt dus niet vast door zijn sinus!
In de praktijk

Een landmeter kan met zijn theodoliet eenvoudig en nauwkeurig hoeken meten (op nauwkeurig!).
Het opmeten van afstanden is veel moeilijker. (Hij moet bijvoorbeeld omlopen omdat er een heg of een sloot is.) Hij beperkt zich tot het nauwkeurig meten van één afstand. Om de overige afstanden te bepalen, meet hij hoeken. De afstanden berekent hij dan met trigonometrie (= driehoeksmeting; het Griekse woord γόνυ (gonu) betekent hoek). Dat heet in de landmeetkunde voorwaartse insnijding.
Deze methode kun je alleen in de “lagere geodesie” gebruiken, de landmeetkunde waarbij het aardoppervlak als plat kan worden beschouwd. Hoe het werkt, heb je bijvoorbeeld in opgave 26 gezien. In opgave 41 zie je weer een voorbeeld van deze werkzijze.
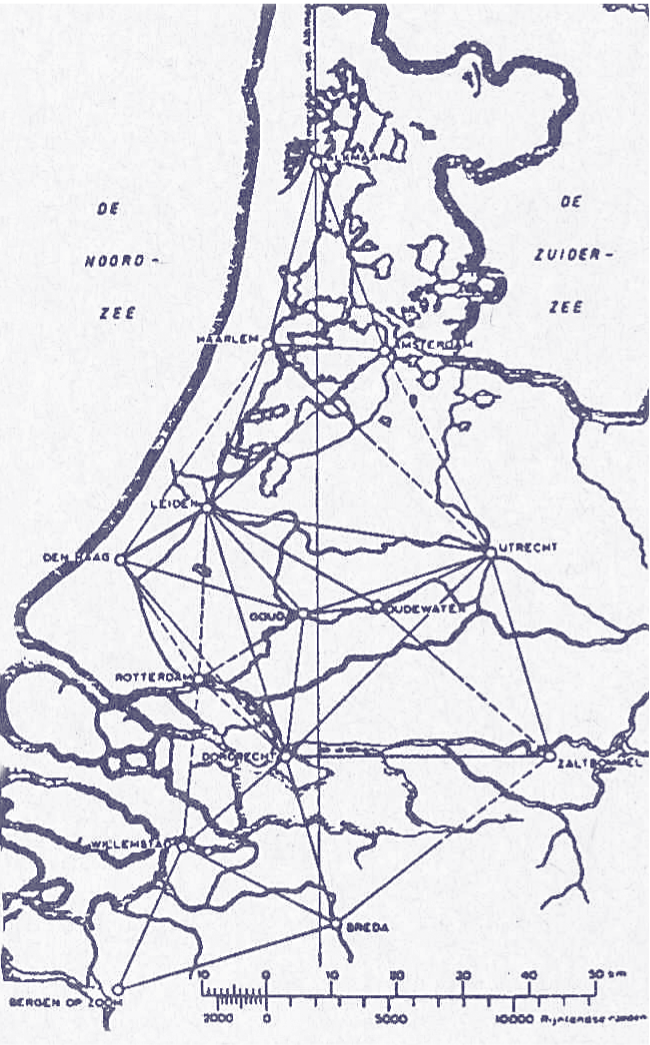
De eerste driehoeksmeting werd uitgevoerd door Willebrord Snel van Royen uit Leiden. Hij bepaalde de afstand tussen Bergen op Zoom en Alkmaar met behulp van een netwerk van aaneengesloten driehoeken tussen torens in veertien steden. Op al deze punten voerde hij richtingsmetingen naar enkele van de andere torens uit. Onder andere in een weiland bij Leiden werd door hem een basis (afstand) gemeten waarmee hij, via een aantal hulpdriehoeken, de grootte van het driehoeksnet bepaalde.
Uit: 175 jaar kadaster GEO-INFO 2007-5
Bij de berekeningen die hierbij uitgevoerd moesten worden, moet je denken aan die in de volgende opgave.
Een landmeter weet dat de afstand tussen en m is. Hij wil de afstand van tot weten. In , en meet hij hoeken. De resultaten zie je in de tekening.
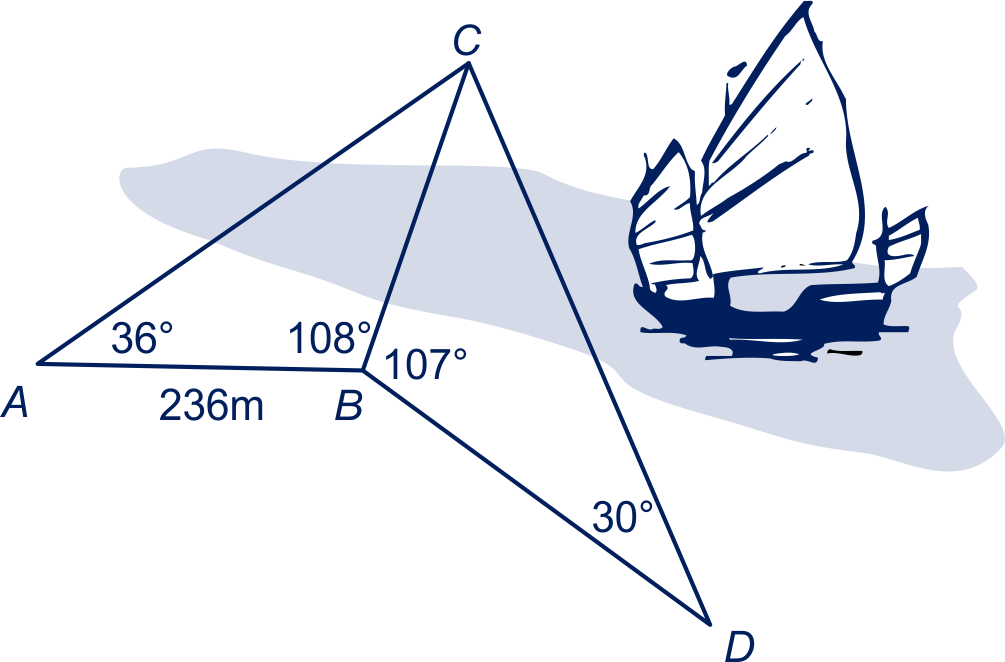
Bereken in één decimaal.
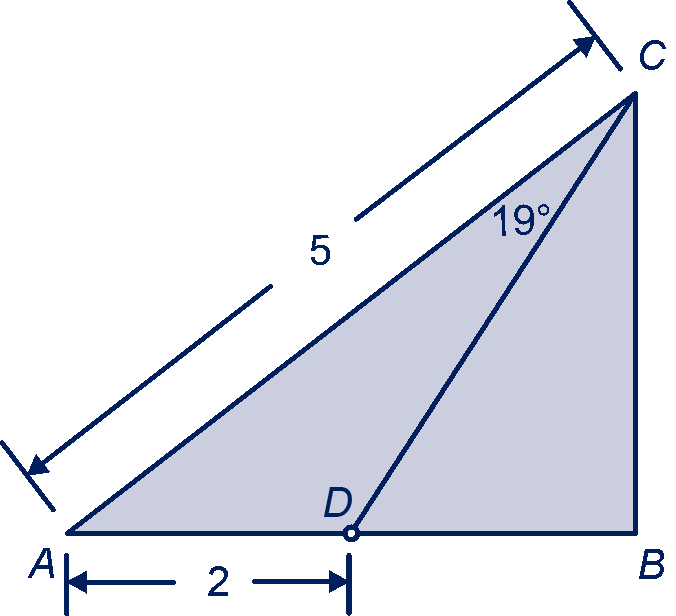
Driehoek is rechthoekig in . De schuine zijde . Op lijnstuk ligt zó, dat . Er geldt: . Zie figuur.
Bereken hoek in graden nauwkeurig.
Bereken de rechthoekszijden van driehoek in één decimaal.
Van driehoek is gegeven: α , en .
Teken driehoek zo nauwkeurig mogelijk. Er zijn twee mogelijkheden, één waarbij hoek stomp is en één waarbij hoek scherp is.
Wat is het verband tussen de scherpe hoek in de ene driehoek en de stompe hoek in de andere?
Bereken sin(β). Welke mogelijkheden voor β volgen hieruit?
Bereken γ en voor het geval dat hoek scherp is en ook voor het geval dat hoek stomp is.
