Teken een driehoek met zijden en en hoek tussen die zijden .
Er is maar één driehoek met deze eigenschappen. De derde zijde ligt vast. Je kunt hem niet met de sinusregel berekenen, probeer maar. Dat kan wel met de cosinusregel. Die behandelen we in deze paragraaf.
Teken een driehoek met zijden van , en .
Er is maar één driehoek met deze eigenschappen. De hoeken liggen dus vast. In de volgende onderdelen gaan we ze berekenen.
Het is ook een voorbereiding op het bewijs van de cosinusregel in de volgende opgave.
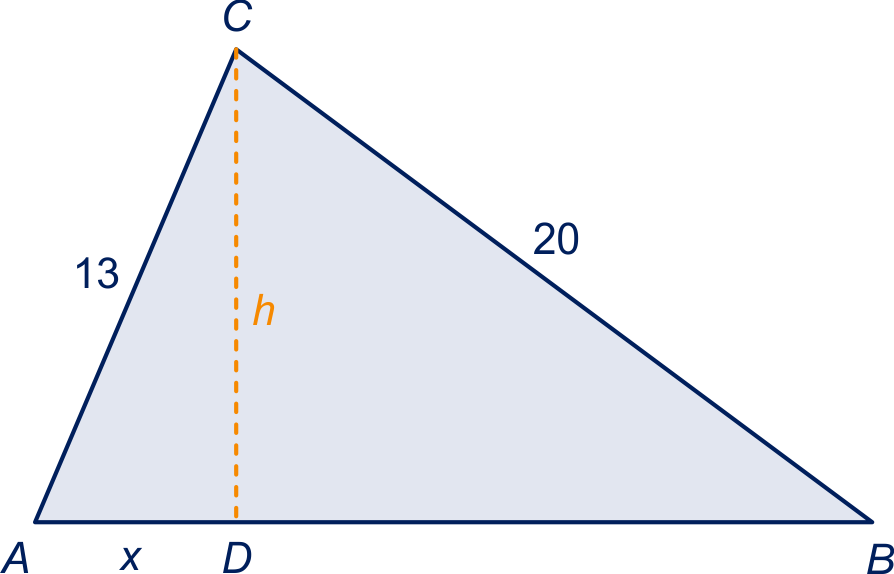
De driehoek uit het vorige onderdeel staat hiernaast. Het hoekpunt tegenover de zijde heet , tegenover de zijde heet en tegenover de zijde heet . is de hoogtelijn uit , met op lijnstuk . noemen we en noemen we . Verder zie plaatje.
Toon aan: en .
Ga na dat hieruit volgt: en bereken hieruit en .
Bereken de hoeken van driehoek in graden nauwkeurig.
In de volgende opgave bewijzen we de cosinusregel.
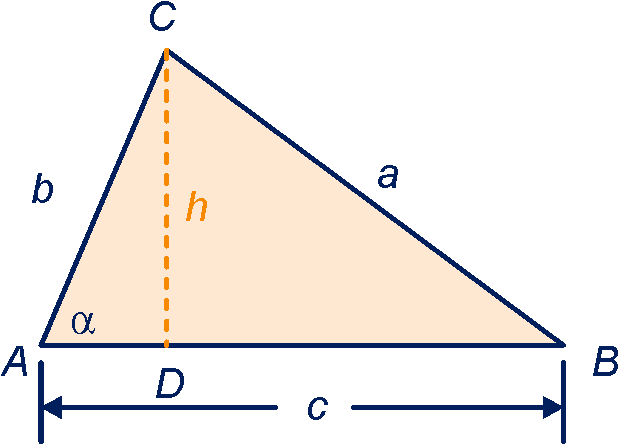
Bekijk de driehoek. is de hoogtelijn uit van driehoek .
Er geldt: , ga dat na.
In het volgende schrijven we, om haakjes te vermijden, in plaats van .
Laat zien dat: en .
Haakjes wegwerken geeft:
.
Waarom geldt nu: ?
Laat zien dat: .
Door de rollen van bijvoorbeeld en te verwisselen krijg je , enzovoort.
Cosinusregel
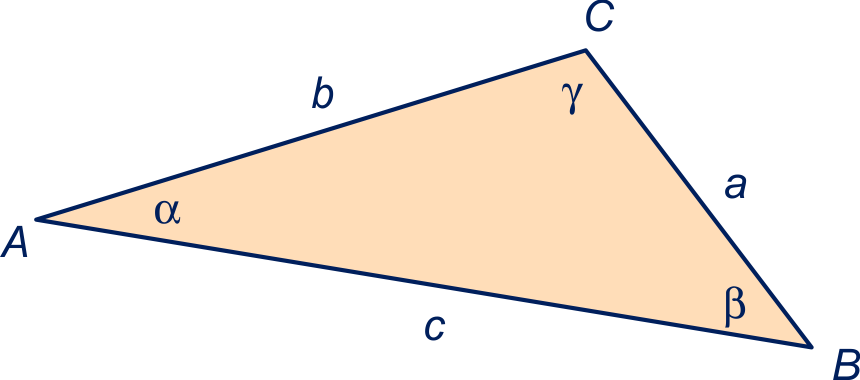
In opgave 45 ligt de hoogtelijn uit tussen en , maar als stomp is ziet het er zó uit.
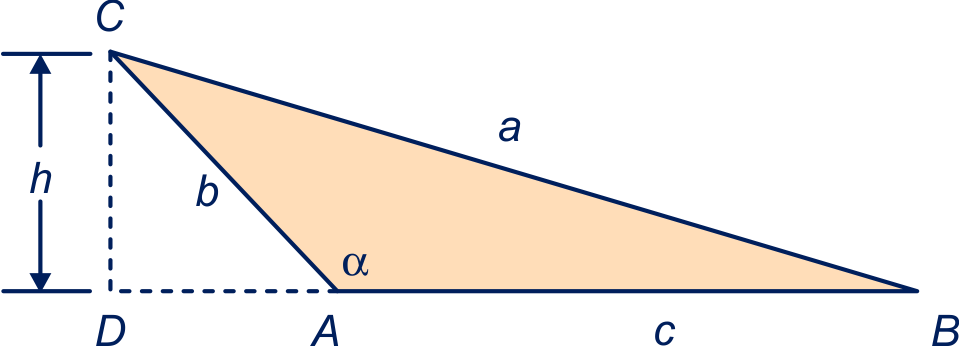
Ook in dit geval gelden de regels als hierboven. Het bewijs staat in Extra opgave 11.
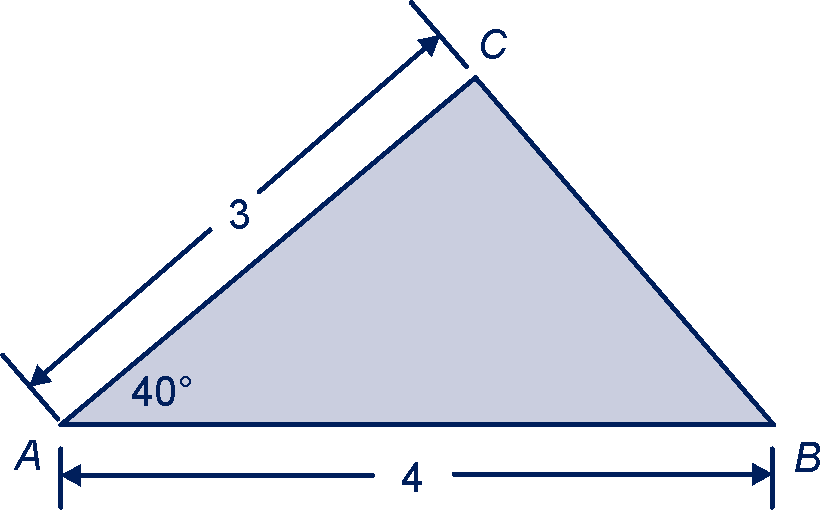
Hiernaast staat de driehoek die je in opgave 44a moest tekenen.
Vraag
Bereken in één decimaal en de hoeken en in graden nauwkeurig.
Oplossing
We noemen en
.
De zijden tegenover de hoeken
, en
noemen we
, en .
We gebruiken de regel: .
Invullen geeft: , dus
.
Om te berekenen, kun je bijvoorbeeld de regel
gebruiken.
Wij gebruiken de sinusregel.
Invullen in geeft:
, dus
, dus
hoek is .
Dus hoek is .
Voorbeeld
In opgave 44b moest je een driehoek tekenen met zijden ,
en .
In het laatste onderdeel van die opgave moest je de hoeken van die driehoek in graden nauwkeurig berekenen. Daar hebben we dat gedaan door een hoogtelijn van de driehoek te tekenen. Maar het kan nu ook direct met de cosinusregel.
We berekenen als voorbeeld de hoek tegenover de zijde van lengte .
Volgens de cosinusregel geldt: .
Dus en
.
Welke regel moet ik toepassen?

We hebben eigenlijk zes regels om zijden of hoeken in driehoek te berekenen.
Je probeert ze alle zes. Als er, na invullen, twee onbekenden in zo'n regel blijven staan, kun je hem niet direct gebruiken. In dat geval probeer je een andere regel.
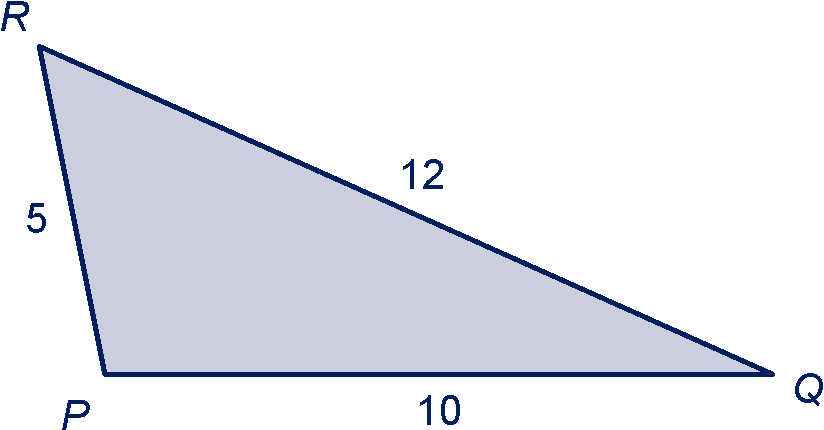
Zie plaatje.
Vraag
Bereken hoek in graden nauwkeurig.
Oplossing
Een 'sinusregel' gebruiken heeft geen zin, want je kent geen enkele hoek.
We passen de regel toe, met , en , dan is .
Je krijgt: , dus en
hoek is .
Gegeven zie figuur 1.
Bereken de lengte van de diagonalen van het parallellogram in twee decimalen.

figuur 1
|
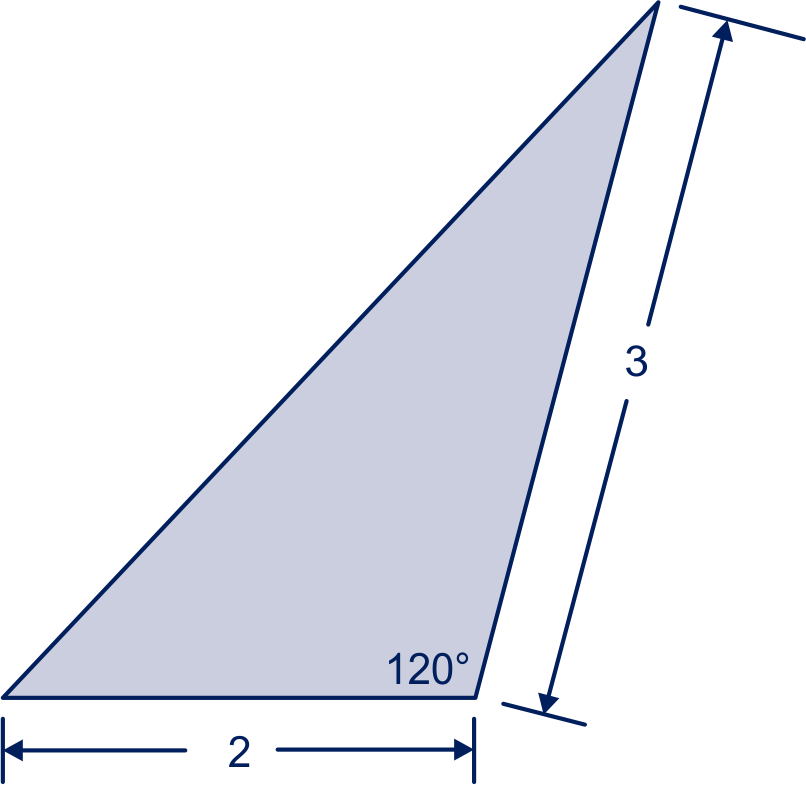
figuur 2
|
Gegeven zie figuur 2.
Bereken de lengte van de zijde tegenover de hoek van exact.
Bereken de zijden en de hoeken met een vraagteken in de volgende figuren.
Geef zo mogelijk een exact antwoord, rond anders af op één decimaal.
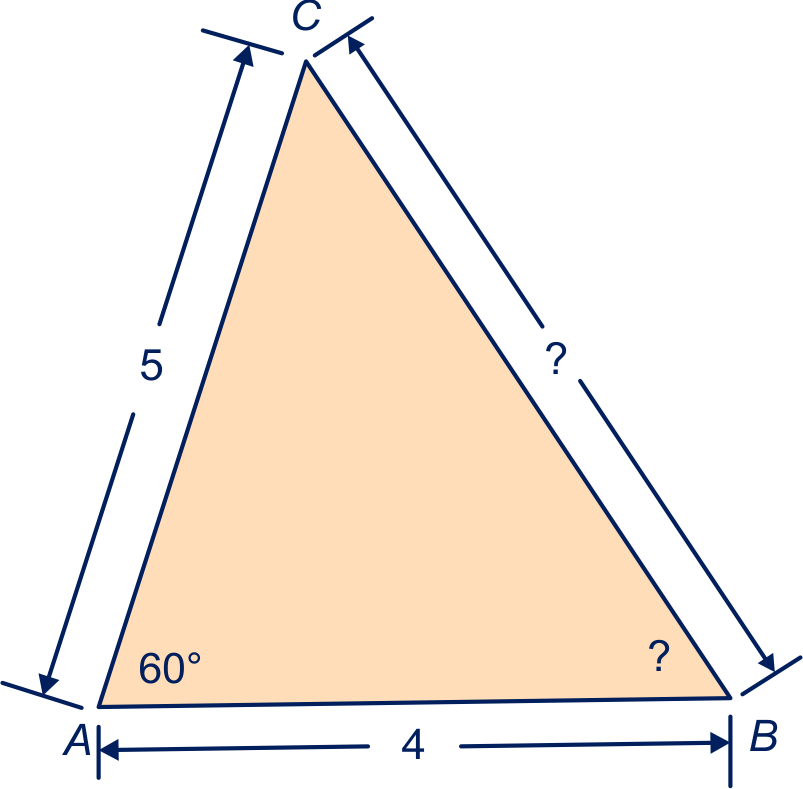
|
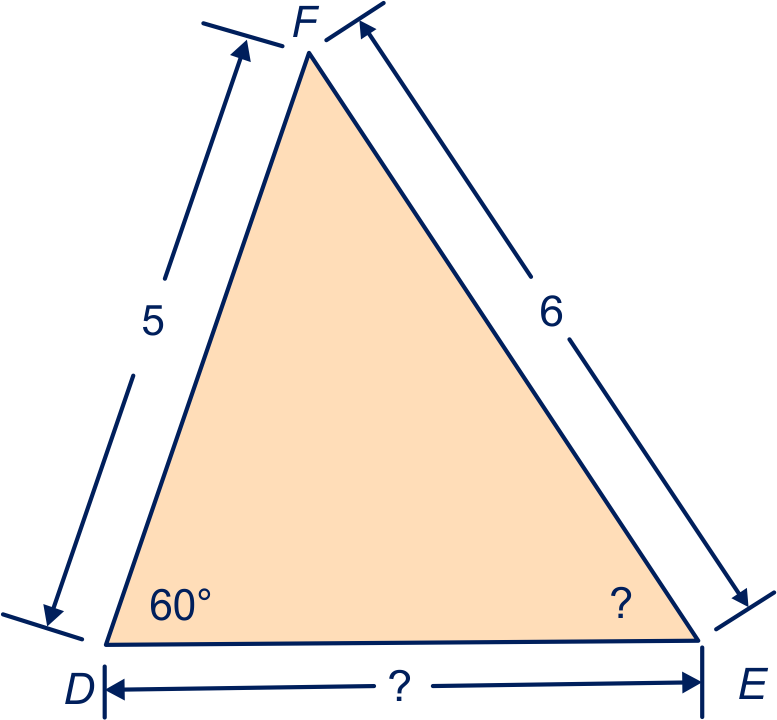
|
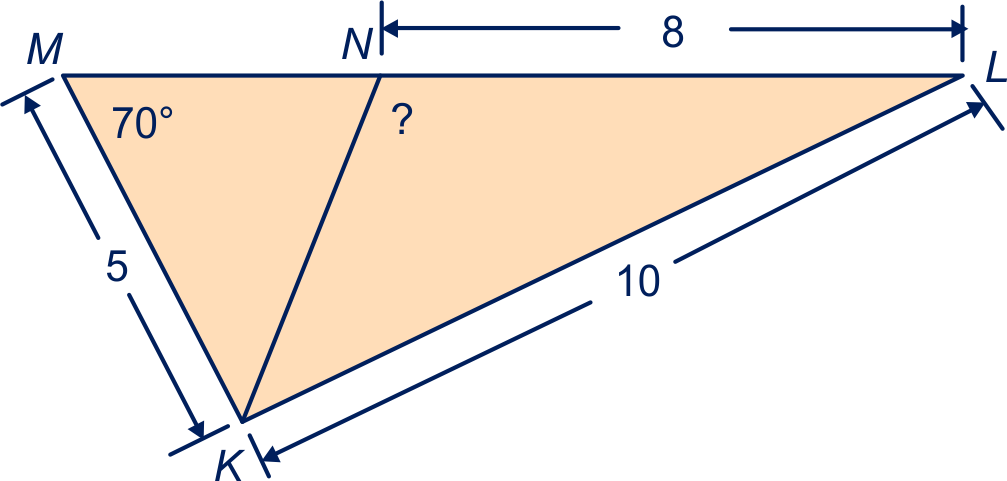
|
In driehoek zijn de zijden , , en de hoeken , , . In elk van de volgende onderdelen zijn drie van de zes gegeven.
|
|
|
|
|
|
|
|
|
|||||
Bereken zo mogelijk de andere drie. Rond de hoeken en de zijden af op een decimaal.
Van de vlieger staan de gegevens in de figuur.
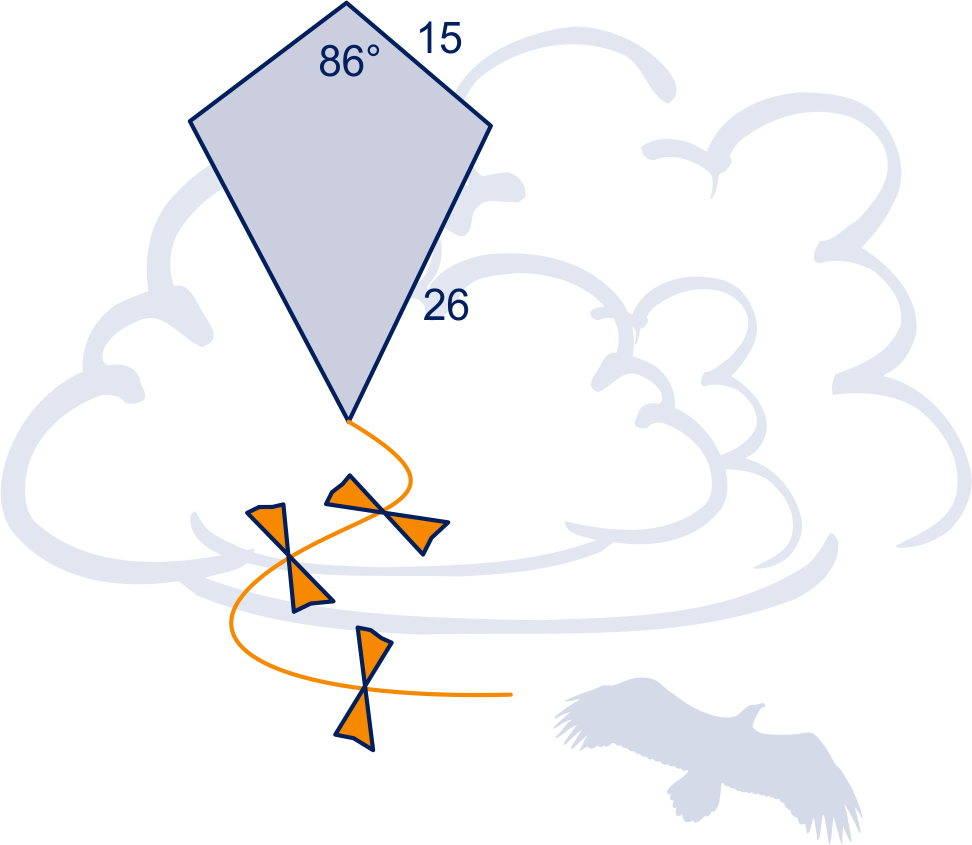
Bereken de lengte van de korte diagonaal in één decimaal nauwkeurig. Doe dat op twee manieren: mét en zonder cosinusregel.
Bereken de andere hoeken van de vlieger in graden nauwkeurig.
Bereken de lengte van de lange diagonaal.
