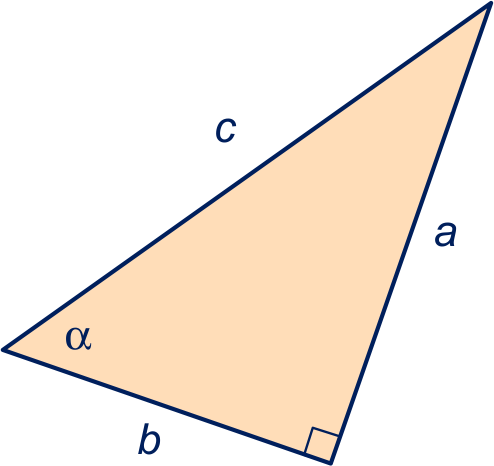
Hoofdstukken > Berekeningen in een driehoek

Herhaling

Sinus, cosinus en tangens van een scherpe hoek, zeg α, hebben we als volgt gedefinieerd.
Maak een rechthoekige driehoek waarvan één van de hoeken de scherpe hoek α is.
De rechthoekszijde tegenover de hoek α noemen we $a$ .
De rechthoekszijde waar α aanligt, noemen we $b$ . De schuine zijde noemen we $c$ .
Dan sin(α) = $\frac{a}{c}$ , cos(α) = $\frac{b}{c}$ en tan(α) = $\frac{a}{b}$ .

Welke rechthoekige driehoek je bij α maakt doet er niet toe.

Bekijk nog eens de driehoek van opgave 9.

Ga na dat in de driehoeken $A D E$ en $A B C$ de verhouding $\frac{overstaande rechthoekszijde}{schuine zijde}$ voor hoek α hetzelfde is.

Dit volgt natuurlijk uit gelijkvormigheid van de twee driehoeken.

Dus sin(α) = $\frac{5}{13}$ . Bereken hieruit met je rekenmachine α in één decimaal.

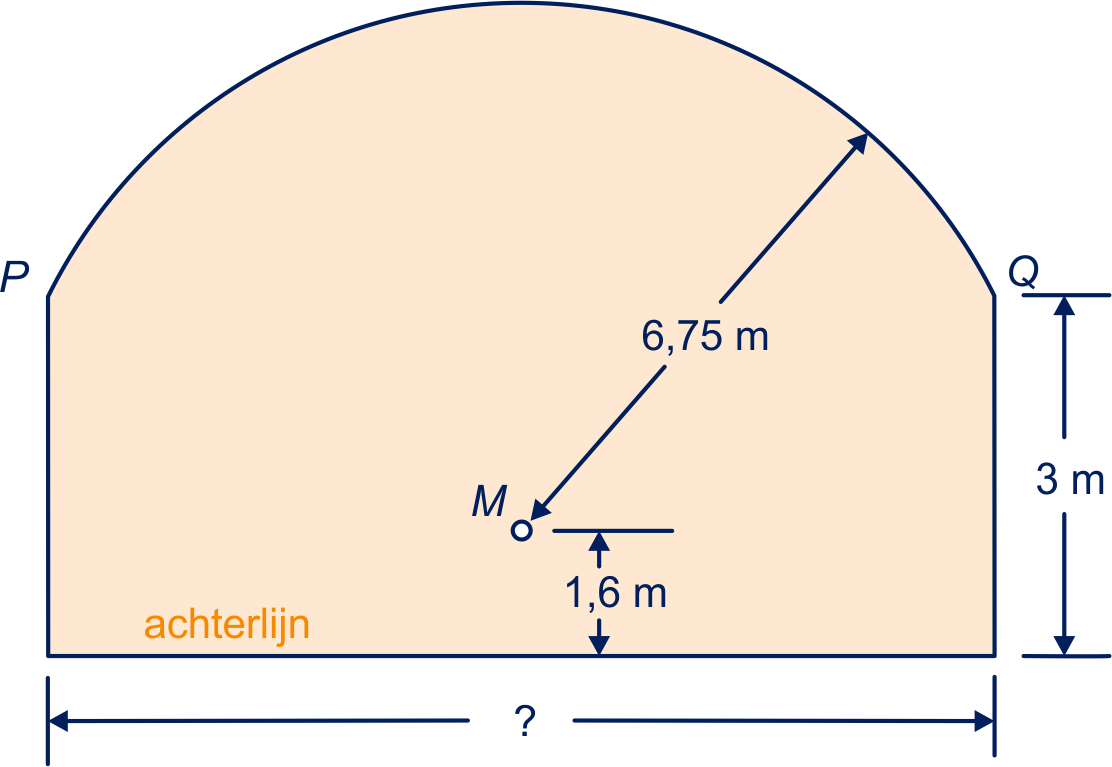
Hiernaast is nog eens een driepuntslijn getekend. $P$ en $Q$ zijn de overgangspunten van 'recht' naar 'krom'.

Bereken hoek $P M Q$ in twee decimalen.

(hint)

Zie opgave 1a: bereken eerst hoek

R M S

Bereken de lengte van de driepuntslijn in dm nauwkeurig.

(hint)

Gebruik de opmerking die na deze opgave komt.

Opmerking:

$A$ en $B$ zijn punten op een cirkel met straal $r$ en middelpunt $M$ . Neem aan: $∠ A M B = α$ graden.
Dan is de lengte van boog $A B$ : $\frac{α}{360} \cdot 2 π r$ .

Meestal gebruik je sinus en cosinus in de volgende vorm.

$a$ = $c \cdot$ sin(α) en $b$ = $c \cdot$ cos(α)

In een rechthoekige driehoek is één van de hoeken $25 °$ . De schuine zijde is $20$ .

Bereken in één decimaal de rechthoekszijden van de driehoek.

Een rechhoekige driehoek heeft een hoek van $54 °$ , de rechthoekszijde tegenover deze hoek heeft lengte $12$ .

Bereken de schuine zijde in één decimaal.

We gaan verder met de driehoek uit de vorige opgave. Het middelpunt $M$ van de cirkel $z$ die door de hoekpunten van de driehoek gaat, is het midden van de schuine zijde.

Leg dat uit.

De hoekpunten van de driehoek noemen we $A$ , $B$ en $C$ , waarbij hoek $B$ recht is en hoek $A$ $54 °$ .

Toon aan: $∠ A M B = 72 °$ .

Bereken de lengte van het stuk van cirkel $z$ tussen de punten $B$ en $C$ in één decimaal.

Sinus, cosinus en tangens zijn alleen gedefinieerd voor scherpe hoeken (tussen $0$ en $90$ graden). In het volgende zullen we deze ook definiëren voor stompe hoeken (tussen $90 °$ en $180 °$ ).

Koershoek

Vier plaatsen liggen op afstand $3$ van $O$ . De koershoeken ten opzichte van het oosten, tegen de wijzers van de klok in zijn achtereenvolgens $47 °$ , $163 °$ , $260 °$ en $294 °$ .

Hoeveel liggen die plaatsen oostelijk en noordelijk van $O$ ? Als een plaats westelijk of zuidelijk van $O$ ligt, gebruik je een negatief getal.

Je komt in plaats $X$ door vanuit $O$ ten opzichte van het oosten met koershoek α over een afstand $r$ lopen. Hierbij is α scherp.

Hoeveel ligt $X$ oostelijk van $O$ en hoeveel noordelijk?

Het antwoord uit b nemen we over voor alle draaihoeken α.
Dus als je met koershoek $163 °$ vanuit $O$ loopt over afstand $3$ , kom je $3 \cdot \sin (163 °)$ noordelijk en $3 \cdot \cos (163 °)$ oostelijk van $O$ .

Wat is het verband tussen $\sin (163 °)$ en $\sin (17 °)$ ? En tussen $\cos (163 °)$ en $\cos (17 °)$ ?

Geef ook het verband tussen $\sin (260 °)$ en $\sin (80 °)$ en tussen $\cos (260 °)$ en $\cos (80 °)$ .

Ook tussen $\sin (294 °)$ en $\sin (66 °)$ en tussen $\cos (294 °)$ en $\cos (66 °)$ .

Een punt dat exact noordelijk op afstand $3$ van $O$ ligt, ligt $3 \cdot \cos (90 °)$ oostelijk van $O$ en $3 \cdot \sin (90 °)$ noordelijk van $O$ .

Wat is dus $\cos (90 °)$ en wat is $\sin (90 °)$ ?

Wat moeten we afspreken voor $\cos (180 °)$ en $\sin (180 °)$ ?

Opmerking:

Voorlopig gebruiken we de sinus en cosinus voor hoeken in driehoeken, dus voor hoeken tussen $0$ en $180$ graden.

Afspraak cos(stompe hoek) en sin(stompe hoek)

Als $90 ° <$ α $< 180 °$ dan:	sin(α) $=$ sin ( $180 ° -$ α)
	cos(α) $=$ $‐$ cos( $180 ° -$ α)
Verder	$\cos (90 °) = 0$ en $\sin (90 °) = 1$ ,
	$\cos (180 °) = ‐ 1$ en $\sin (180 °) = 0$ .

sin(α) $=$ sin( $83 °$ ) en α is stomp.

Bepaal α zonder rekenmachine. (Je antwoord mag je met je rekenmachine controleren.)

cos(α) $=$ $‐$ cos( $83 °$ ) en α is stomp.

Bepaal α zonder rekenmachine.

Van een hoek α tussen $0 °$ en $90 °$ is gegeven: sin(α) $= 0,7$ .

Zoek met de GR een hoek α in twee decimalen met sin(α) $= 0,7$ .

De GR geeft een scherpe hoek. Er is ook een stompe hoek α met sin(α) $= 0,7$ .

Voor welke stompe hoek α geldt: sin(α) $= 0,7$ ?

Voor een hoek α tussen $0 °$ en $180 °$ geldt: cos(α) $= ‐ 0,2$ .

Bepaal α met de GR. Zijn er meer mogelijkheden?

Sinus en cosinus in speciale gevallen

Sinus en cosinus van een gegeven hoek kun je met je rekenmachine vinden. In speciale gevallen hebben kun je ze ook exact berekenen.
Dat doen we in de volgende opgaven.

$A B C D$ is een vierkant met zijden $10$ . Hoek $C A B$ noemen we α.

Bereken $A C$ en α exact. Vereenvoudig de wortel.
Meer over vereenvoudigen van wortels vind je in de paragraaf Rekentechniek.

Bereken sin(α) en cos(α) exact. Vereenvoudig je antwoorden.

$A B C$ is een regelmatige driehoek met zijden $6$ . $M$ is het midden van $A B$ . Hoek $C A M$ noemen we α en hoek $A C M$ noemen we β.

Hoe groot zijn α en β?

Bereken sin(α), cos(α), sin(β) en cos(β) exact. Vereenvoudig je antwoorden.

Met de vorige twee opgaven kun je de volgende tabel maken.

	$30 °$	$45 °$	$60 °$
sin	$\frac{1}{2}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2} \sqrt{3}$
cos	$\frac{1}{2} \sqrt{3}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2}$

Maak een tabel zoals hieronder en vul de exacte waarden in, zonder rekenmachine.

	$90 °$	$120 °$	$135 °$	$150 °$	$180 °$
sin
cos

Controleer enkele antwoorden met de GR.

Van een hoek α tussen $0 °$ en $180 °$ is gegeven: sin(α) $= \frac{1}{2}$ .

Hoe groot is α (zonder GR)?

Van een hoek β tussen $0 °$ en $180 °$ is gegeven: cos(β) $= \frac{1}{2}$ .

Hoe groot is β?

Van een hoek γ tussen $0 °$ en $180 °$ is gegeven: cos(γ) $= ‐ \frac{1}{2}$ .

Hoe groot is γ?

Anne loopt vanuit een punt $P$ met koershoek $53 °$ over een afstand van $4$ km.
Bernie vanuit $P$ met koershoek $173 °$ , ook $4$ km.

Bereken exact hoe ver Anne en Bernie dan van elkaar verwijderd zijn.

(hint)

Noem de punten waar Anne en Bernie zich dan bevinden

A

B

en het punt daar midden tussen

M

; je kunt

A M

exact berekenen.