$(\mathrm{2,}\mathrm{‐}3),(\mathrm{2,3}),(\mathrm{‐}\mathrm{2,3}),(a,\mathrm{‐}b)$

$(\mathrm{‐}a,b),(b,a),(\mathrm{‐}b,\mathrm{‐}a),(\mathrm{‐}a,\mathrm{‐}b)$

-

Klopt.

$x\left(\frac{1}{t}\right)=\frac{3\cdot \frac{1}{t}}{1+{\left(\frac{1}{t}\right)}^3}\cdot \frac{t^3}{t^3}=\frac{3t^2}{t^3+1}=y\left(t\right)$. Hier volgt ook uit dat $y\left(\frac{1}{t}\right)=x\left(t\right)$.

Dat betekent dat hij symmetrisch is in de lijn $y=x$.

$x=\frac{3\cdot \frac{y}{x}}{1+{\left(\frac{y}{x}\right)}^3}\iff x+\frac{y^3}{x^2}=\frac{3y}{x}$. Beide kanten met $x^2$ vermenigvuldigen geeft het resultaat.

Als $(a,b)$ aan de vergelijking voldoet, dan ook $(b,a)$, dus de figuur is symmetrisch in de lijn $y=x$.

$(\mathrm{97,1002})$ terugschuiven naar de eerste figuur, dus over $\left(\begin{array}{c}3\\ \mathrm{‐}2\end{array}\right)$, dit geeft het punt $(\mathrm{100,1000})$. Dit punt voldoet aan de vergelijking van de eerste figuur.

$x=x_{\text{oud}}-3$, $y=y_{\text{oud}}+2$, dus $y_{\text{oud}}=y-2$ en $x_{\text{oud}}=y+3$.

${(y-2)}^2={(x+3)}^3$

-

${(y+1)}^2={(x-3)}^3$

Vergelijking van de cirkel met middelpunt $O$ en straal $r$ is: $x^2+y^2=r^2$. Als je $x$ vervangt door $x-a$ en $y$ door $y-b$, krijg je de vergelijking ${(x-a)}^2+{(y-b)}^2=r^2$, dat is een vergelijking van de cirkel met middelpunt $(a,b)$ en straal $r$. Klopt.

Je krijgt de vergelijking $y-b={(x-a)}^2$ oftewel $y={(x-a)}^2+b$, dat is een parabool met top $(a,b)$.

$2x+3y=13$

Bij verschuiven over $\left(\begin{array}{c}\mathrm{‐4}\\ 4\end{array}\right)$ komt $(\mathrm{3,1})$ in $(\mathrm{‐}\mathrm{1,5})$, dus schuift $k$ naar $m$.

$2(x+4)+3(y-4)=9\iff 2x+3y=13$, klopt.

$x(\mathrm{‐}t)=x(t)$ en $y(\mathrm{‐}t)=\mathrm{‐}y(t)$.

Zeg je bent op tijdstip $t$ in $(a,b)$, dan ben je op $\mathrm{‐}t$ in $(a,\mathrm{‐}b)$. Dus als $(a,b)$ op de baan, dan ook $(a,\mathrm{‐}b)$.
De baan is symmetrisch in de $x$-as.

$y^2=\frac{4}{9}{t}^6-5\frac{1}{3}{t}^4+16t^2=\frac{4}{9}{x}^3-5\frac{1}{3}{x}^2+16x$

Als $(a,b)$ aan de vergelijking voldoet, dan ook $(a,\mathrm{‐}b)$, want ${(\mathrm{‐}b)}^2=b^2$.

In de lijn $y=\mathrm{‐}x$. Het punt $\left(a,b\right)$ heeft dan als beeld $\left(\mathrm{‐}b,\mathrm{‐}a\right)$. Je krijgt dus de vergelijking ${(\mathrm{‐}x)}^2=\frac{4}{9}{(\mathrm{‐}y)}^3-5\frac{1}{3}{(\mathrm{‐}y)}^2+16\cdot \mathrm{‐}y$, dus
$x^2=\mathrm{‐}\frac{4}{9}{y}^3-5\frac{1}{3}{y}^2-16y$.

Laat $(x,y)$ een punt van de kromme in figuur 3 zijn en $(x_{\text{oud}},y_{\text{oud}})$ zijn origineel, dan geldt: $x=\frac{1}{3}{x}_{\text{oud}}$ en $y=y_{\text{oud}}$, dus $x_{\text{oud}}=3x$ en dus geldt:
$y^2=\frac{4}{9}{(3x)}^3-5\frac{1}{3}{(3x)}^2+16\cdot 3x$, dus een vergelijking is: $y^2=12x^3-48x^2+48x$.

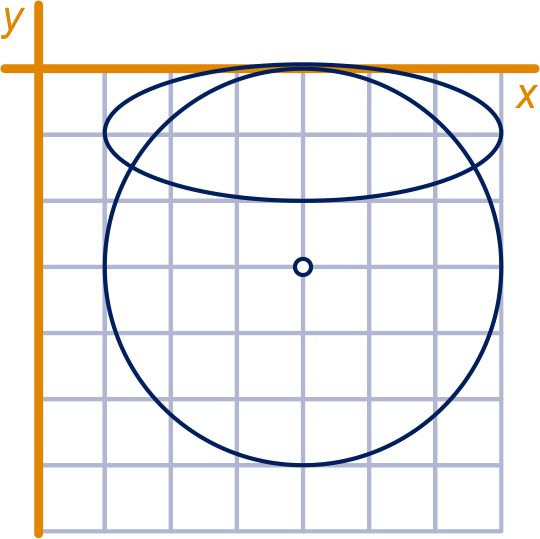
Als $(a,b)$ aan de vergelijking voldoet, dan ook $(b,a)$, dus als $\left(a,b\right)$ op de ellips ligt, dan ook $\left(b,a\right)$.

Stel de figuur wordt verschoven over $\left(\begin{array}{c}a\\ a\end{array}\right)$, dan wordt de vergelijking:
${(x-a)}^2-(x-a)(y-a)+{(y-a)}^2+3(x-a)+3(y-a)=4$.
$(\mathrm{‐3,0})$ moet aan deze vergelijking voldoen.
Dit leidt tot de vergelijking $a^2-3a-4=0$, dus $a=4$ of $a=\mathrm{‐1}$.
Dus verschuiven over $\left(\begin{array}{c}\mathrm{‐}1\\ \mathrm{‐}1\end{array}\right)$ of $\left(\begin{array}{c}4\\ 4\end{array}\right)$.

$x^2+{(2y)}^2=20$

Met de $x$-as: $y=0\iff x=\pm 2\sqrt{5}$, dus de snijpunten zijn: $(\pm 2\sqrt{5}\mathrm{,0})$.
Met de $y$-as: $x=0\iff y=\pm \sqrt{5}$, dus de snijpunten zijn: $(\mathrm{0,}\pm \sqrt{5})$.

-

$y=2{\left(x-1\frac{1}{2}\right)}^2+\frac{1}{2}$

Over $\left(\begin{array}{c}1\frac{1}{2}\\ \frac{1}{2}\end{array}\right)$.

$(\cos (t)\mathrm{,2}\sin (t))$

Verticaal met factor $2$.

$x^2+{(\frac{1}{2}y)}^2=1\iff 4x^2+y^2=4$

Verticaal vermenigvuldigen met $\frac{1}{3}$.

Zie figuur op de volgende bladzijde.

Dat zijn de lijnen $x-4=0$ en $3y+3=0$.

$x-4=0\iff {(3y+3)}^2=9\iff y=0\text{ of }y=\mathrm{‐}2$, dus de verticale as heeft lengte $2$.
$3y+3=0\iff {(x-4)}^2=9\iff x=1\text{ of }x=7$, dus de horizontale as heeft lengte $6$.
Of: als je verticaal vermenigvuldigt, blijft de lengte van horizontale as de diameter van de cirkel, dus $6$ en de lengte van de verticale as wordt $\frac{1}{3}\cdot 6=2$.

figuur bij opgave 45