Voor het gemak nemen we in deze paragraaf de tijd in seconden en de afstand in cm.
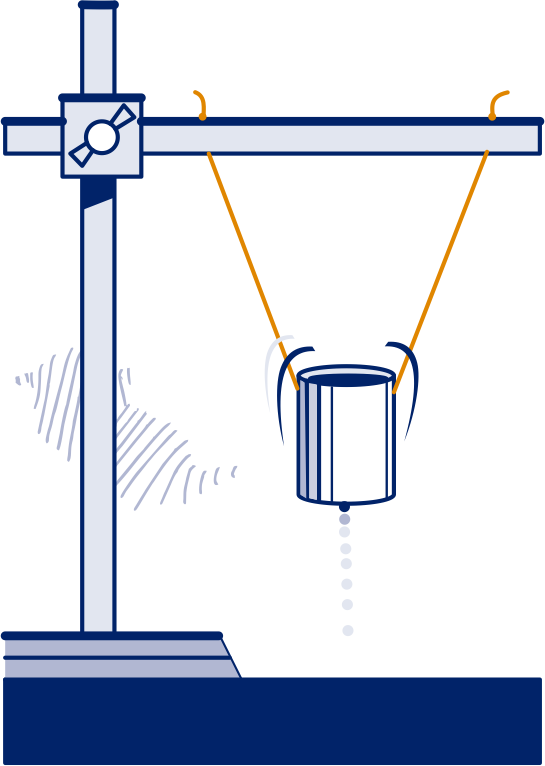
Neem een blikje met een klein gaatje in de bodem. Hang het op zoals hiernaast getekend is. Vul het blikje met zout. Geef het een duwtje in een schuine richting en bekijk het zoutpatroon dat ontstaat. Een dergelijk patroon noemen we een Lissajousfiguur.
Een Lissajousfiguur ontstaat door een punt aan twee onderling loodrechte harmonische bewegingen te laten deelnemen. We kunnen dit patroon in GeoGebra (of op de GR) zichtbaar maken.

Jules Antoine Lissajous, een Frans natuurkundige, deed onderzoek naar trillingen, een populair onderwerp in die tijd. Hij maakte trillingen zichtbaar, bijvoorbeeld door een vibrerende stemvork in het water te houden of door een lichtbundel te laten schijnen op een spiegel die aan een trillende stemvork was vastgemaakt.
Een mooi voorbeeld van een Lissajousfiguur is de lemniscaat.
Een punt is horizontaal onderhevig aan de trilling:
en verticaal aan de trilling:
.
Horizontaal is de frequentie (het aantal periodes per seconde) en de amplitude (maximale uitwijking uit de evenwichtsstand) .
Verticaal is de frequentie en de amplitude .
De kromme is dus geparametriseerd door:
, met
.
Teken de beweging op de GR of in GeoGebra.
Bepaal met een exacte berekening de coördinaten van de hoogste en de laagste punten van de baan. Geef ook de tijdstippen waarop deze punten bereikt worden.
Bereken exact de snelheidsvector, uitgedrukt in .
Wat voor bijzonders merk je op over de snelheidsvector in de hoogste en de laagste punten van de baan?
Bepaal exact de uiterste punten 'links' en 'rechts' van de baan en de tijdstippen waarop ze bereikt worden. Wat kun je over de snelheidsvector zeggen op die momenten?
Bepaal de exacte momenten waarop de beweging door de oorsprong gaat. Met welke snelheid gaat dat?
Een kogeltje neemt deel aan twee harmonische trillingen. Het resultaat is de Lissajousfiguur hieronder. Bij enkele punten is vermeld wanneer het kogeltje daar langs komt.
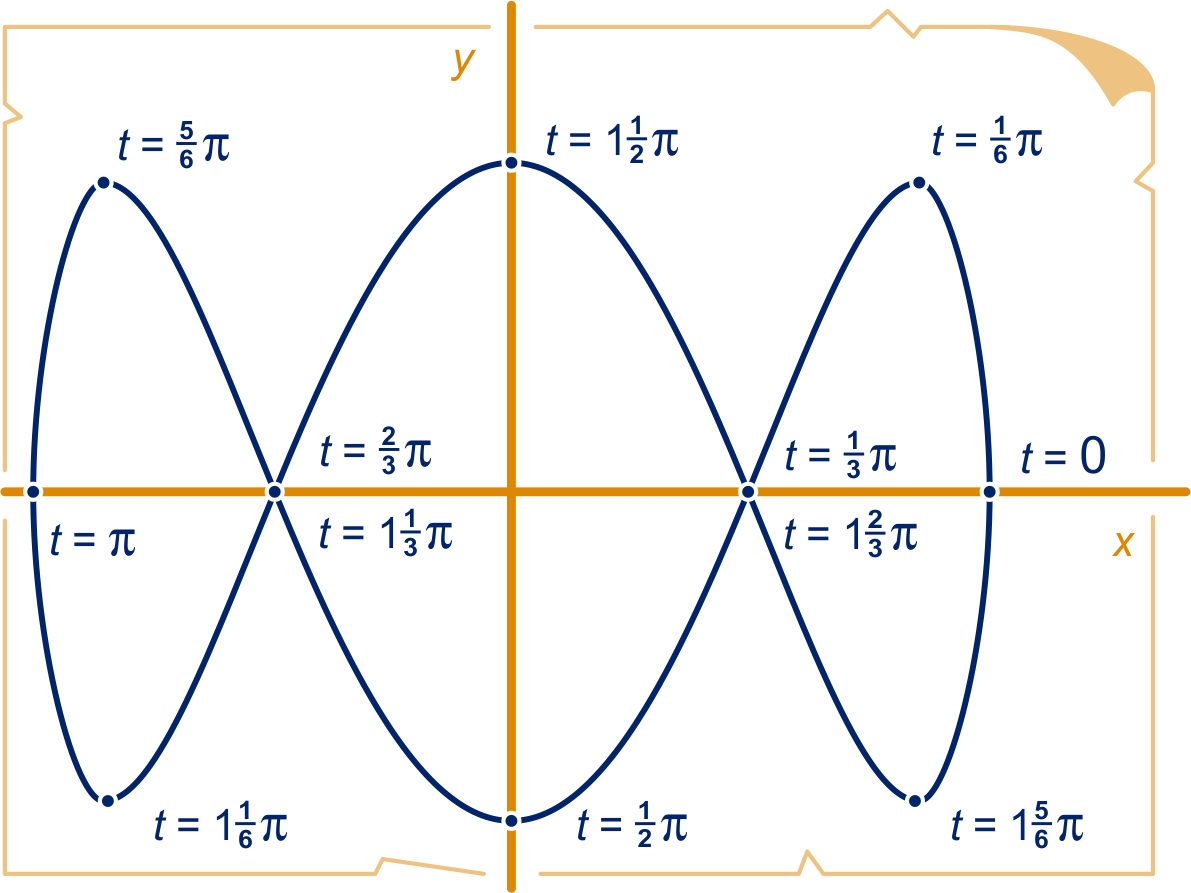
De -coördinaat van punten van de baan neemt alle waarden aan van tot en met . De -coördinaat neemt alle waarden aan van tot en met . De -coördinaat en de -coördinaat zijn, als functie van , harmonische bewegingen. We noemen die en .
Wat is de amplitude van en van ?
Van zowel de grafiek van als van de grafiek van ken je dertien punten op het interval .
Schets de grafieken van en op grond hiervan.
Geef de formules van en .
Als je het goed gedaan hebt, kun je de Lissajousfiguur in GeoGebra (of de GR) tekenen.
Doe dat.
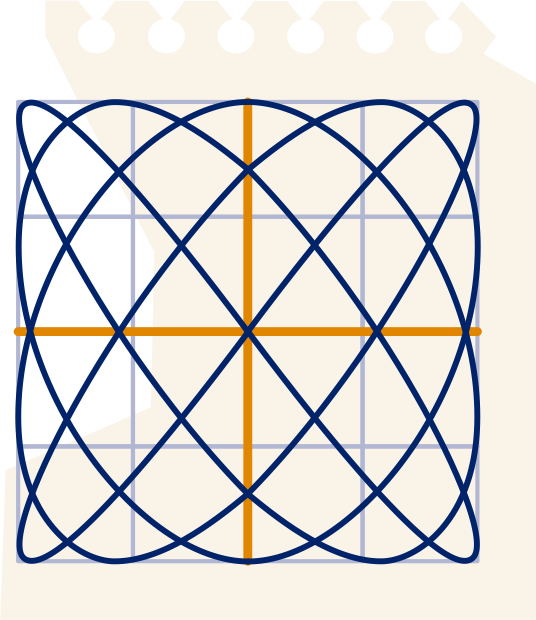
De Lissajousfiguur hiernaast is opgesloten in het vierkant met hoekpunten
,
,
en
.
De beweging ontstaat door een punt te laten deelnemen aan tegelijkertijd uitgevoerde trillingen in de
- en de -richting.
Je krijgt de hele figuur in het tijdsinterval .
Uit het aantal keren dat de rand geraakt wordt, kun je het aantal periodes van de trillingen in de - en de
-richting bepalen.
Doe dat.
Zoek een parametervoorstelling van de baan en controleer je formules in GeoGebra. (Het is het gemakkelijkst om als startpunt te kiezen).
In het volgende bekijken we de beweging van een punt met bewegingsvergelijkingen: ,
voor gehele waarden van
en .
We laten lopen van tot
, dan is de baan zeker 'af'.
Teken enkele banen met GeoGebra. Maak schuiven voor en , met en (met stapgrootte ).
Hieronder zie je drie voorbeelden.
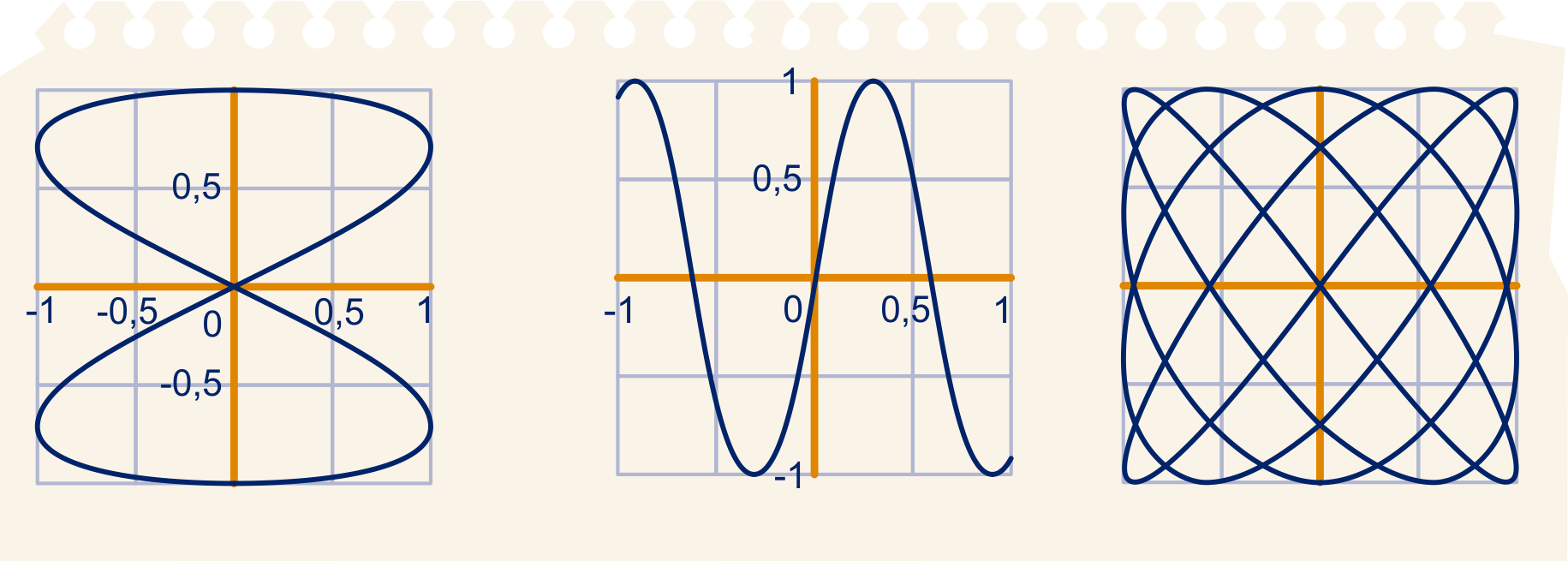
Neem bijvoorbeeld ,
dan krijg je de Lissajousfiguur linksboven.
De lijn
snijdt de figuur in twee punten.
Bereken de coördinaten van die punten.
De lijn snijdt de figuur in vier punten.
Bereken de coördinaten van die punten.
Als je een verticale lijn
of horizontale lijn ,
met
, bij een Lissajousfiguur trekt, kom je meestal
meerdere snijpunten tegen.
Waarom is dat zo?
Door de Lissajousfiguur linksboven verticaal met een geschikte positieve factor te vermenigvuldigen, is de hoek tussen de raaklijnen in de oorsprong .
Bereken die factor langs algebraïsche weg.
Neem en varieer .
Voor diverse waarden van doorsnijdt de figuur zichzelf op de negatieve -as.
Bereken exact onder welke hoek dat gebeurt in het geval .
Laat met een berekening zien dat de snelheidsvector in alle gevallen
op tijdstip (en dus ook op tijdstip ) horizontaal
gericht is.
Wat is de grootte van de snelheid op dat moment?
Als je en kiest, zie je het bewegende punt op bepaalde tijdstippen stilstaan.
Bereken die tijdstippen exact.
Laat met een algebraïsche berekening zien dat het bewegende punt op geen enkel moment stilstaat als en .
De combinaties van en waarbij de figuur geen vloeiende gesloten kromme is, blijken precies de gevallen te zijn waarbij snelheid voorkomt.
Heb je daar een verklaring voor?
Gegeven is voor elke gehele waarde van de kromme: .
Voer deze krommen in in GeoGebra.
Voor welke waarde(n) van gaan de krommen door ? Laat langs algebraïsche weg zien dat je antwoord, juist is.
De krommen zien er uit als gewone grafieken! Verticale lijnen snijden de kromme maar één keer.
Toon aan dat aan.
Voor is de figuur een deel van de grafiek van een kwadratische functie.
Toon dat aan en geef een formule voor die functie.
