$40t-5t^2=0\iff 5t(t-8)=0\iff t=0$ of $t=8$, dus na $8$ seconden.

$\frac{1}{2-1}\cdot \left(\begin{array}{c}40-20\\ 60-35\end{array}\right)=\left(\begin{array}{c}20\\ 25\end{array}\right)$, $\frac{1}{\mathrm{1,5}-1}\cdot \left(\begin{array}{c}30-20\\ \mathrm{48,75}-35\end{array}\right)=\left(\begin{array}{c}20\\ \mathrm{27,5}\end{array}\right)$,
$\frac{1}{\mathrm{1,01}-1}\cdot \left(\begin{array}{c}\mathrm{20,2}-20\\ \mathrm{35,2995}-35\end{array}\right)=\left(\begin{array}{c}20\\ \mathrm{29,95}\end{array}\right)$

Zie figuur hieronder links.

$\left(\begin{array}{c}20\\ 30\end{array}\right)$

De gemiddelde snelheidsvector tussen de tijdstippen $2$ en $\mathrm{2,01}$ is
$\frac{1}{\mathrm{2,01}-2}\cdot \left(\begin{array}{c}\mathrm{40,2}-40\\ \mathrm{60,1995}-60\end{array}\right)=\left(\begin{array}{c}20\\ \mathrm{19,95}\end{array}\right)$. De snelheidsvector op tijdstip $2$ is (ongeveer) $\left(\begin{array}{c}20\\ 20\end{array}\right)$, zie figuur hieronder midden.

$\left(\begin{array}{c}20\\ 40-10t\end{array}\right)$

Zie de figuur hieronder rechts.

Zie figuur hieronder rechts.

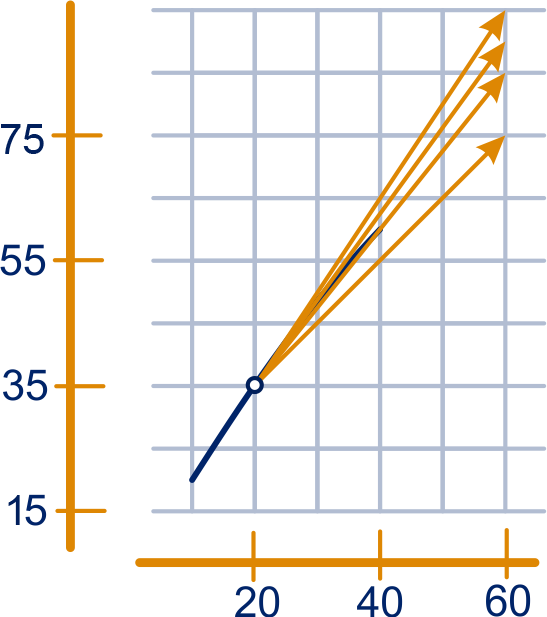
figuur bij opgave 1c

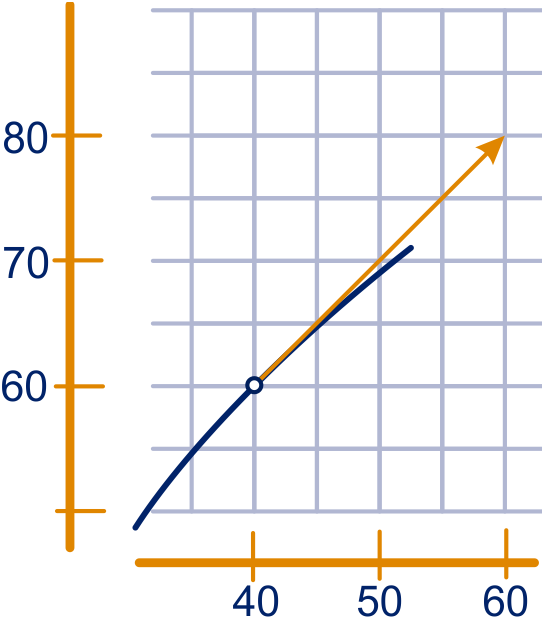
figuur bij opgave 1e

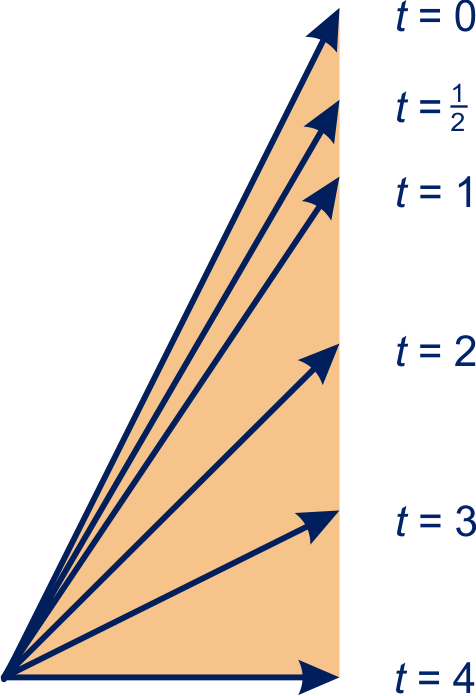
figuur bij opgave 2b,c

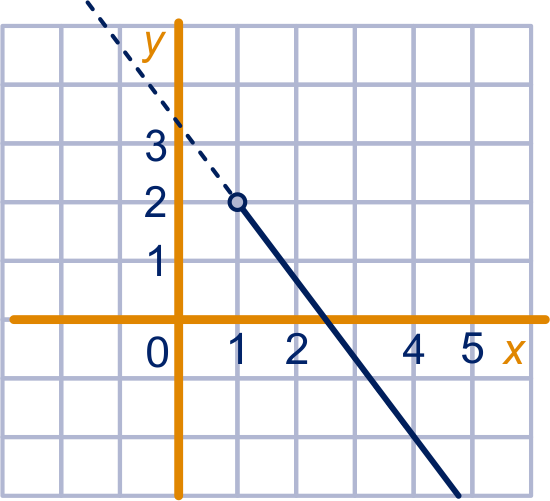
$P$ beweegt over de lijn $4x+3y=10$, vul maar in. De eerste coördinaat van $P$ neemt alle waarden $\ge 1$ aan en de tweede alle waarden $\le 2$.

$4x+3y=10$ en $y\le 2$ of
$4x+3y=10$ en $x\ge 1$.

$\left(\begin{array}{c}6t\\ \mathrm{‐}\text{8}t\end{array}\right)$

De snelheid is $\sqrt{36t^2+64t^2}=10\text{|}t\text{|}$; dus op $t=1$ en $t=\mathrm{‐}1$. Dan is $P$ in $(\mathrm{4,}\mathrm{‐}2)$.

Zie hieronder.

$\frac{1}{t_2-t_1}\cdot \left(\begin{array}{c}1+2t_2-\text{(}1+2t_1\text{)}\\ 2-4t_2-\text{(}2-4t_1\text{)}\end{array}\right)=$
$\frac{1}{t_2-t_1}\cdot \left(\begin{array}{l}2t_2-2t_1\\ 4t_1-4t_2\end{array}\right)=\left(\begin{array}{c}2\\ \mathrm{‐}4\end{array}\right)$

$\tan (\text{α})=2$, dus $\text{α}\approx 63°$.

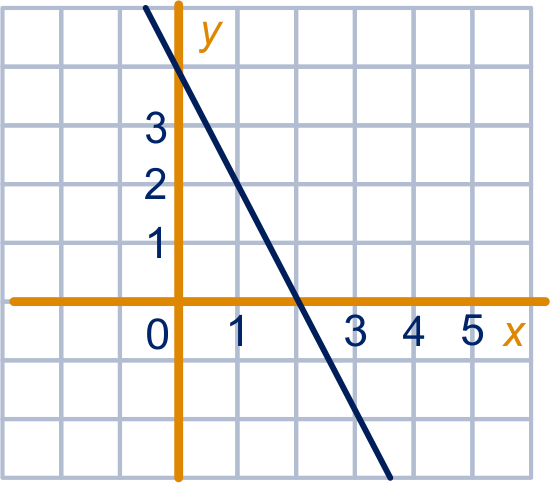
figuur bij opgave 4a

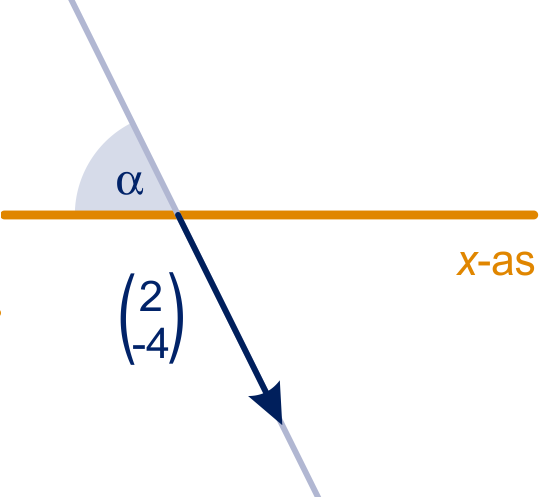
figuur bij opgave 4c

Naar beneden

Met de $x$-as:
$y=0\iff \frac{2}{3}t(t^2-6)=0\iff t=\mathrm{0,}\sqrt{6},\mathrm{‐}\sqrt{6}$, dit geeft de punten $(\mathrm{0,0})$ en $(\mathrm{6,0})$.
Met de $y$-as:
$x=0\iff t=0$. Dit geeft het punt $(\mathrm{0,0})$.

$\left(\begin{array}{c}2t\\ 2t^2-4\end{array}\right)$

Horizontaal als $2t^2-4=0\iff t=\sqrt{2}$ of $t=\mathrm{‐}\sqrt{2}$, dus in $(\mathrm{2,}\mathrm{‐}2\frac{2}{3}\sqrt{2})$ en in $(\mathrm{2,}2\frac{2}{3}\sqrt{2})$.
Verticaal in $(\mathrm{0,0})$.

$\sqrt{4t^4-12t^2+16}$

Op $t=3$ is het punt in $(\mathrm{9,6})$, de snelheidsvector is dan $\left(\begin{array}{c}6\\ 14\end{array}\right)$.

Noem die hoek $\text{α}$, dan $\tan (\text{α})=\frac{14}{6}$, dus $\text{α}\approx 67°$.

$y=2\frac{1}{3}x-15$

Dan zijn de componenten van de snelheidsvector even lang, dus $2t^2-4=2t$ of $2t^2-4=\mathrm{‐}2t$, dus $t=1$, $t=2$, $t=\mathrm{‐}1$ of $t=\mathrm{‐}2$.

Als je in de bewegingsvergelijkingen van opgave 5, $t$ vervangt door $\sqrt[3]{t}$, krijg je de bewegingsvergelijkingen van opgave 7. Verder kan $\sqrt[3]{t}$ alle waarden aannemen.

De snelheidsvector op tijdstip $t$ is: $\left(\begin{array}{c}\frac{2}{3\sqrt[3]{t}}\\ \frac{2}{3}-\frac{4}{3\sqrt[3]{t^2}}\end{array}\right)$. Op $t=27$ is het bewegend punt in $T(\mathrm{9,6})$, de snelheidsvector is dan: $\left(\begin{array}{c}\frac{2}{9}\\ \frac{14}{27}\end{array}\right)$. Als je deze met $27$ vermenigvuldigt, krijg je $\left(\begin{array}{c}6\\ 14\end{array}\right)$.

Als $t=\sqrt{x}$, dan $t^2=x$ en $\frac{2}{3}{t}^3-4t=\frac{2}{3}{\sqrt{x}}^3-4\sqrt{x}$ $=\frac{2}{3}x\sqrt{x}-4\sqrt{x}$.

$f\text{'}\left(x\right)=\sqrt{x}-\frac{2}{\sqrt{x}}$, dus $f\text{'}\left(9\right)=2\frac{1}{3}$ $\to$ $y=2\frac{1}{3}x-15$; je krijgt dus dezelfde raaklijn als in opgave 5c.

$\left(\begin{array}{c}2t\\ 3t^2\end{array}\right)$

Omdat die $\overrightarrow{0}$ is.

$y=x\sqrt{x}$ en $y=\mathrm{‐}x\sqrt{x}$

Van beide functies is de afgeleide in $0$ gelijk aan $0$, dus de richting is horizontaal.