1

a

$(\begin{matrix} 1 \\ 3 \end{matrix})$ en $(\begin{matrix} ‐ 1 \\ ‐ 3 \end{matrix})$

b

$(\begin{matrix} ‐ 2 \\ 1 \end{matrix})$ en $(\begin{matrix} 2 \\ ‐ 1 \end{matrix})$

c

$(\begin{matrix} ‐ 100 \\ 87 \end{matrix})$ en $(\begin{matrix} 100 \\ ‐ 87 \end{matrix})$

2

Ja, ja, ${({\vec{a}}_{R})}_{R} = ‐ \vec{a}$ .

3

Dit volgt uit: $O A^{2} = a^{2} + b^{2}$ , $O P^{2} = p^{2} + q^{2}$ en $A P^{2} = {(p - a)}^{2} + {(q - b)}^{2}$ $= a^{2} - 2 a p + p^{2} + b^{2} - 2 b q + q^{2}$ .

4

$(\begin{matrix} a \\ b \end{matrix})$ en $(\begin{matrix} c \\ d \end{matrix})$ staan loodrecht op elkaar dan en alleen dan als $(\begin{matrix} a \\ b \end{matrix})$ en ${(\begin{matrix} c \\ d \end{matrix})}_{L} = (\begin{matrix} ‐ d \\ c \end{matrix})$ afhankelijk zijn.
Pas nu de stelling na opgave 49 toe.
Of: vergelijk de werkwijze met die in opgave 50.
Dan $(\begin{matrix} c \\ d \end{matrix}) = t \cdot (\begin{matrix} ‐ b \\ a \end{matrix})$ . Veronderstel $b \neq 0$ , dan $t = ‐ \frac{c}{b}$ , dus $d = ‐ \frac{c}{b} \cdot a \Leftrightarrow b d = ‐ c a$ .
Omgekeerd, als $b d = ‐ c a$ mogen we wel weer veronderstellen dat $b \neq 0$ . Neem dan $t = ‐ \frac{c}{b}$ , dan $(\begin{matrix} c \\ d \end{matrix}) = t \cdot (\begin{matrix} ‐ b \\ a \end{matrix})$ .

5

$\vec{v} \cdot \vec{v} = {| \vec{v} |}^{2}$

6

a

$(\begin{matrix} a \\ 3 \end{matrix}) \cdot (\begin{matrix} 4 \\ a + 1 \end{matrix}) = 4 a + 3 a + 3 = 0 \Leftrightarrow a = ‐ \frac{3}{7}$

b

$(\begin{matrix} a \\ 3 \end{matrix}) \cdot (\begin{matrix} a \\ ‐ 4 \end{matrix}) = a^{2} - 12 = 0 \Leftrightarrow a = 2 \sqrt{3}$ of $a = ‐ 2 \sqrt{3}$

7

Het punt $P$ is $(x,0)$ , dan $\vec{A P} = (\begin{matrix} x + 1 \\ ‐ 3 \end{matrix})$ en $\vec{B P} = (\begin{matrix} x - 7 \\ ‐ 4 \end{matrix})$ .
$(\begin{matrix} x + 1 \\ ‐ 3 \end{matrix}) \cdot (\begin{matrix} x - 7 \\ ‐ 4 \end{matrix}) = 0 \Leftrightarrow x^{2} - 6 x + 5 = 0 \Leftrightarrow x = 1$ of $x = 5$ .
Dus $(1,0)$ en $(5,0)$ .

8

a

$(\begin{matrix} x + 3 \\ y \end{matrix}) \cdot (\begin{matrix} x - 3 \\ y \end{matrix}) = 0 \Leftrightarrow x^{2} + y^{2} = 9$

b

Een cirkel met middelpunt $O$ en straal $3$ . Dit volgt ook uit de stelling van Thales.

9

a

$\vec{v} = (\begin{matrix} 3 \\ 1 \end{matrix})$ ;
$C$ krijg je door $B$ over ${\vec{v}}_{L}$ te verschuiven, dus $C = (4 - 1,3 + 3) = (3,6)$ ;
$D$ krijg je door $A$ over ${\vec{v}}_{L}$ te verschuiven, dus $D = (1 - 1,2 + 3) = (0,5)$ .
Zie hieronder.

b

$\vec{v} = (\begin{matrix} 3 \\ ‐ 2 \end{matrix})$ ;
$C$ krijg je door $B$ over ${\vec{v}}_{L}$ te verschuiven, dus $C = (4 + 2,0 + 3) = (6,3)$ ; $D = (6 - 3,3 + 2) = (3,5)$ .
Zie hieronder.

c

$\vec{v} = (\begin{matrix} 61 \\ 63 \end{matrix})$ , $C = (72 - 63,83 + 61) = (9,144)$ ; $D = (9 - 61,144 - 63) = (‐ 52,81)$

figuur bij onderdeel a

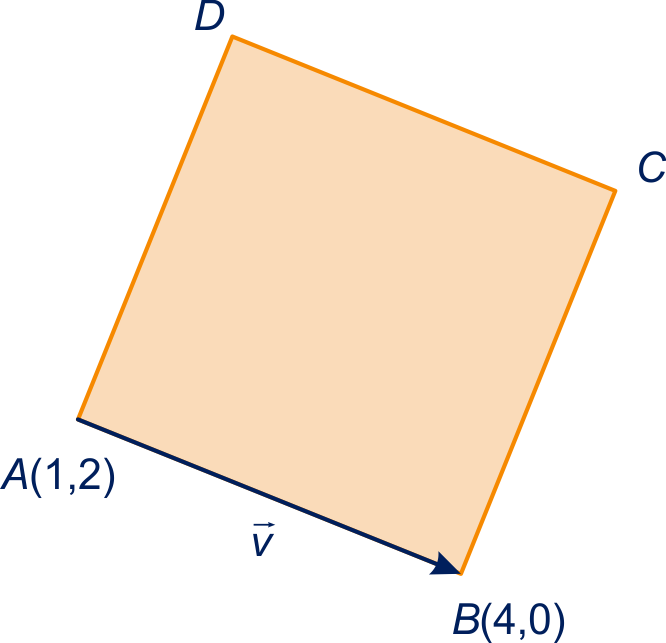
figuur bij onderdeel b

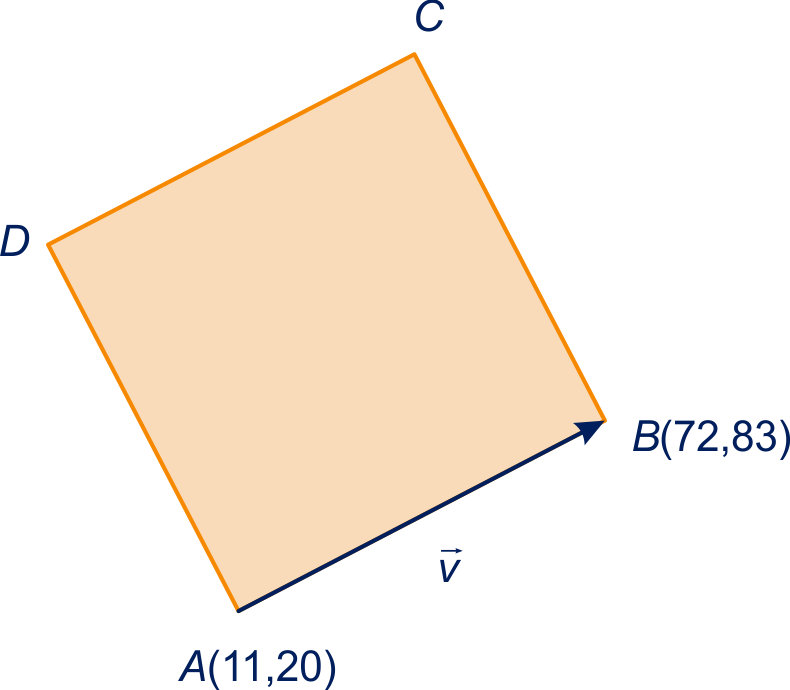
figuur bij onderdeel c

d

Je kunt $C$ over $‐ \vec{A B}$ verschuiven, je vindt: $D = (9 - 61,144 - 63) = (‐ 52,81)$ .

e

$\vec{A B} = (\begin{matrix} 61 \\ ‐ 10 \end{matrix})$ , dus $C = (50 + 10,10 + 61) = (60,71)$ en $D = (60 - 61,71 + 10) = (‐ 1,81)$ .

10

a

$(a_{2} + b_{1} - b_{2}, ‐ a_{1} + b_{1} + b_{2})$

b

$(a_{2} + b_{1} - b_{2} - (b_{1} - a_{1}), ‐ a_{1} + b_{1} + b_{2} - (b_{2} - a_{2})) = (a_{1} + a_{2} - b_{2}, a_{2} - a_{1} + b_{1})$

11

a

Het midden van lijnstuk $A C$ noemen we $M$ . De coördinaten van de punten $B$ en $C$ kun je dan vinden door $M$ over ${\vec{A M}}_{R}$ respectievelijk ${\vec{A M}}_{L}$ te verschuiven.
$M (1,2)$ en $\vec{A M} = (\begin{matrix} 2 \\ 4 \end{matrix})$ , dus $B = (1 + 4,2 - 2) = (5,0)$ ; $D = (1 - 4,2 + 2) = (‐ 3,4)$

b

Zoals in het vorige onderdeel.
$M (‐ 53,57)$ , $\vec{A M} = (\begin{matrix} 57 \\ ‐ 58 \end{matrix})$ , dus $B = (‐ 53 - 58,57 - 57) = (‐ 111,0)$ en
$D = (‐ 53 + 58,57 + 57) = (5,114)$ .

12

a

$a^{2} + b^{2} = 4$

b

$(\frac{1}{2} a, \frac{1}{2} b)$

c

${(\frac{1}{2} a)}^{2} + {(\frac{1}{2} b)}^{2} = \frac{1}{4} \cdot 4 = 1$ , dus het centrum beweegt over een cirkel met straal $1$ en middelpunt $(0,0)$ , maar alleen over het deel in het eerste kwadrant (dus met $x \geq 0$ en $y \geq 0$ ).

d

Zeg $A (a,0)$ , $B (0, b)$ . Het midden $M$ van $A B$ is dan $(\frac{1}{2} a, \frac{1}{2} b)$ . Noem de eindpunten van de andere staaf $C$ en $D$ , dan $C (\frac{1}{2} a - \frac{1}{2} b, \frac{1}{2} b - \frac{1}{2} a)$ en $D (\frac{1}{2} a + \frac{1}{2} b, \frac{1}{2} b + \frac{1}{2} a)$ .

e

De $y$ -coördinaat van $C$ is tegengesteld aan de $x$ -coördinaat van $C$ .
De $y$ -coördinaat van $D$ is gelijk aan de $x$ -coördinaat van $D$ .
Dus $C$ loopt over de lijn $y = ‐ x$ en $D$ over de lijn $y = x$ .

13

a

${\vec{v}}_{L} = (\begin{matrix} ‐ 2 \\ 1 \end{matrix})$ en ${\vec{v}}_{R} = (\begin{matrix} 2 \\ ‐ 1 \end{matrix})$ . Vectoren die een hoek van $45 °$ met $\vec{v}$ maken zijn $\vec{v} + {\vec{v}}_{L} = (\begin{matrix} ‐ 1 \\ 3 \end{matrix})$ en $\vec{v} + {\vec{v}}_{R} = (\begin{matrix} 3 \\ 1 \end{matrix})$ . Deze zijn $\sqrt{2}$ keer zo lang als $\vec{v}$ .

b

Dan moet je $\vec{v} + {\vec{v}}_{R}$ met de factor $\frac{1}{\sqrt{2}} = \frac{1}{2} \sqrt{2}$ vermenigvuldigen, je krijgt $(\begin{matrix} 1 \frac{1}{2} \sqrt{2} \\ \frac{1}{2} \sqrt{2} \end{matrix})$ .

14

a

-

b

$\vec{P A} = (\begin{matrix} ‐ a - 2 \\ ‐ b \end{matrix})$ ; $Q$ krijg je door $A$ over ${\vec{P A}}_{L}$ te verschuiven, dus
$Q = (‐ 2 + b,0 - a - 2) = (‐ 2 + b, ‐ a - 2)$ .
Dan $\vec{Q B} = (\begin{matrix} 4 - b \\ a + 2 \end{matrix})$ en $R$ krijg je door $B$ over ${\vec{Q B}}_{L}$ te verschuiven, dus
$R = (2 - a - 2,0 + 4 - b) = (‐ a,4 - b)$ .

c

Het midden van $P R$ is dan $(\frac{1}{2} a + \frac{1}{2} \cdot ‐ a, \frac{1}{2} b + \frac{1}{2} (4 - b)) = (0,2)$ , hangt dus niet af van $a$ en $b$ .