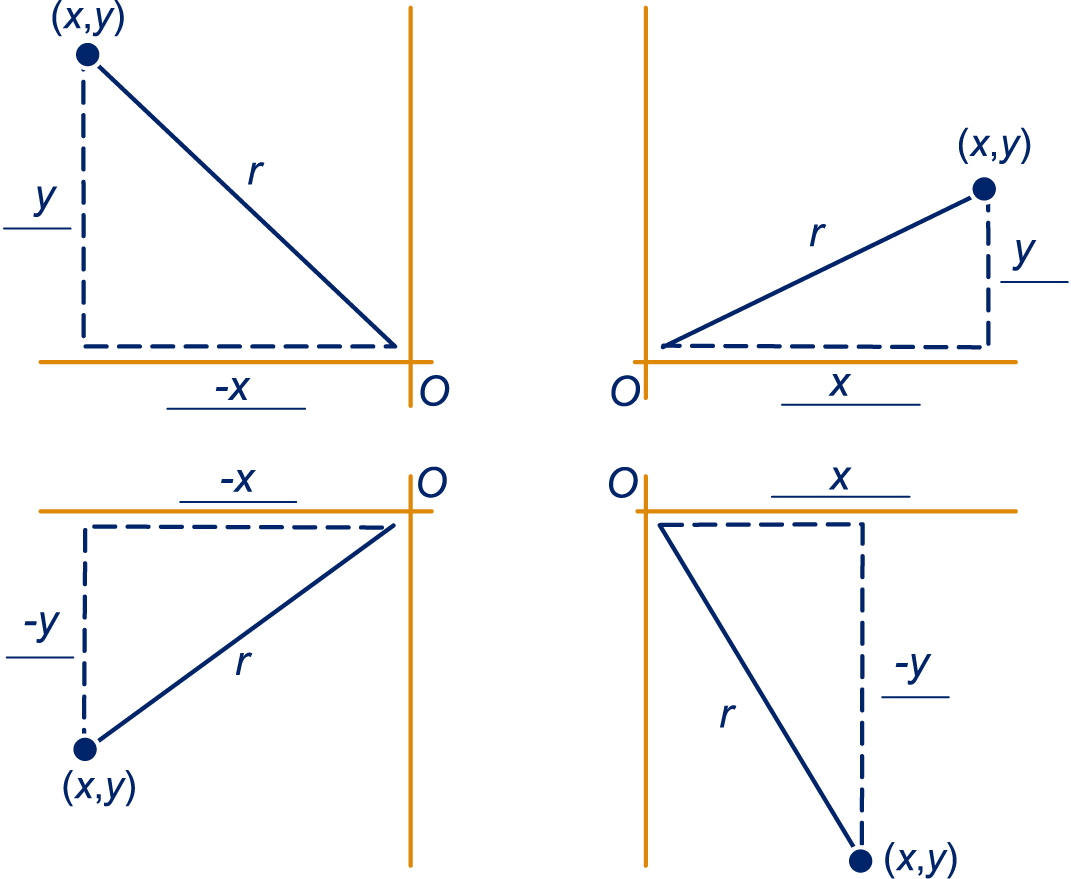
Een cirkel met middelpunt en straal .
Zie de figuur hieronder.
, klopt
Zie de figuur hieronder.
Dan , dus , dus
of.
Dus en .
Zie de figuur hieronder.
en
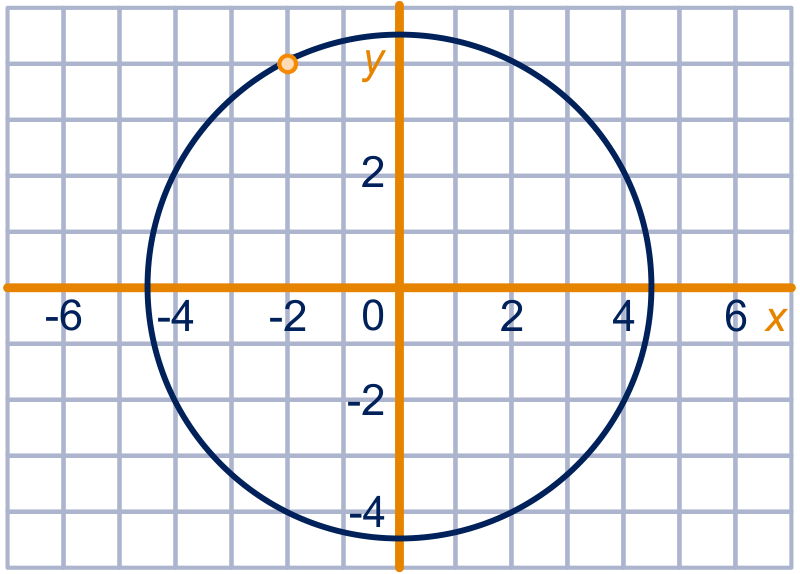
figuur bij opgave 30ac
|
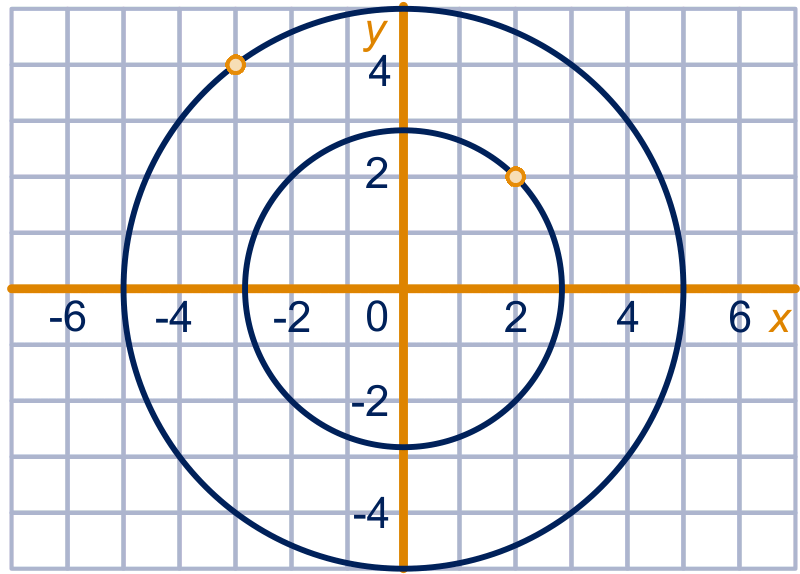
figuur bij opgave 31a
|
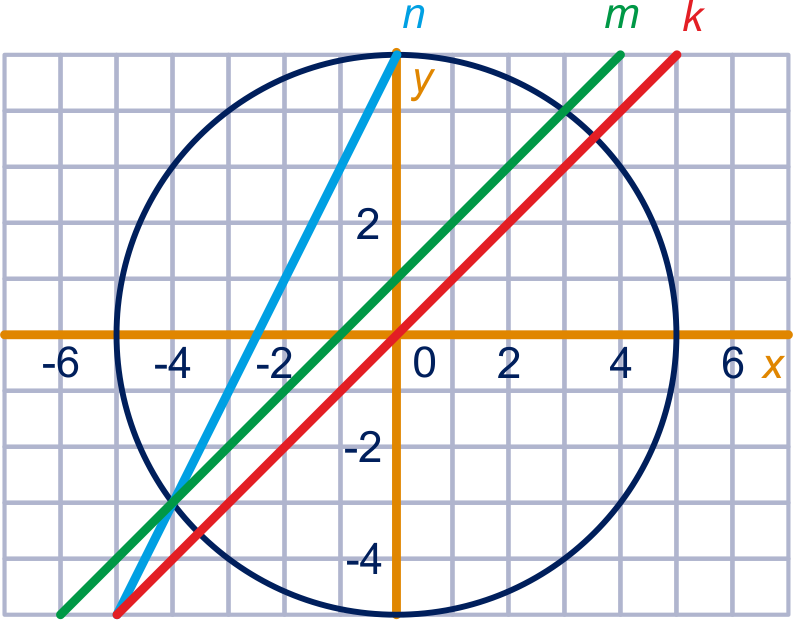
, , , , , , enzovoort.
Zie opgave b.
, oftewel
of
Snijpunten en .
Zie opgave b.
|
of |
||
Zie opgave b.
Snijpunt is
of
Snijpunten en .
Niet één.
kun je schrijven als
.
Dit laatste houdt in dat
afstand tot
heeft.
-
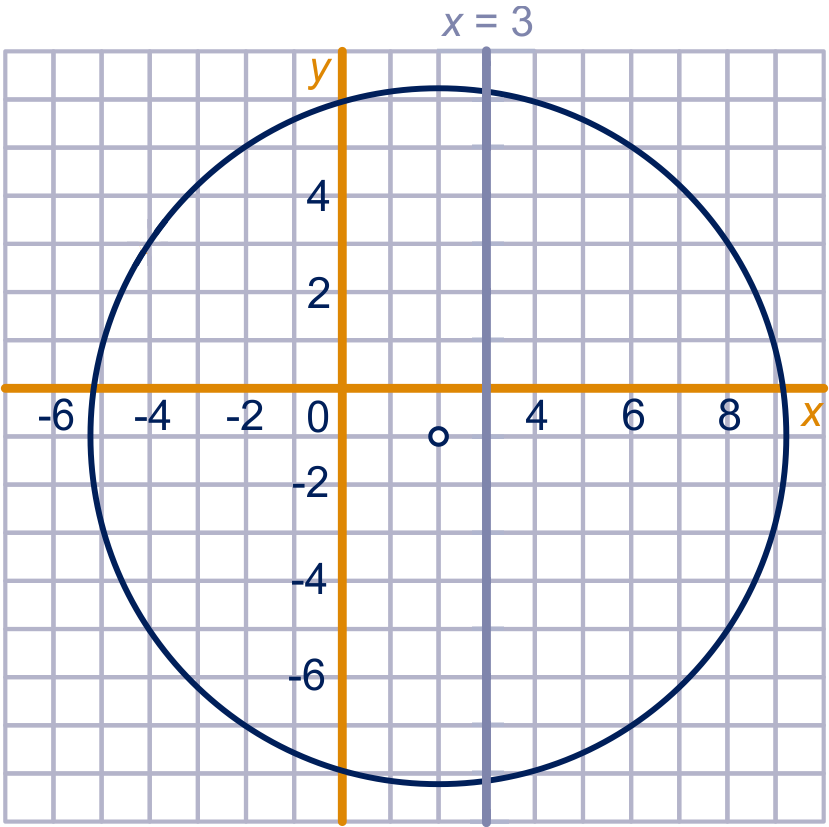
of
of
Snijpunten en .
, dus
of
of
Snijpunten en .
Zie de figuur links hieronder.
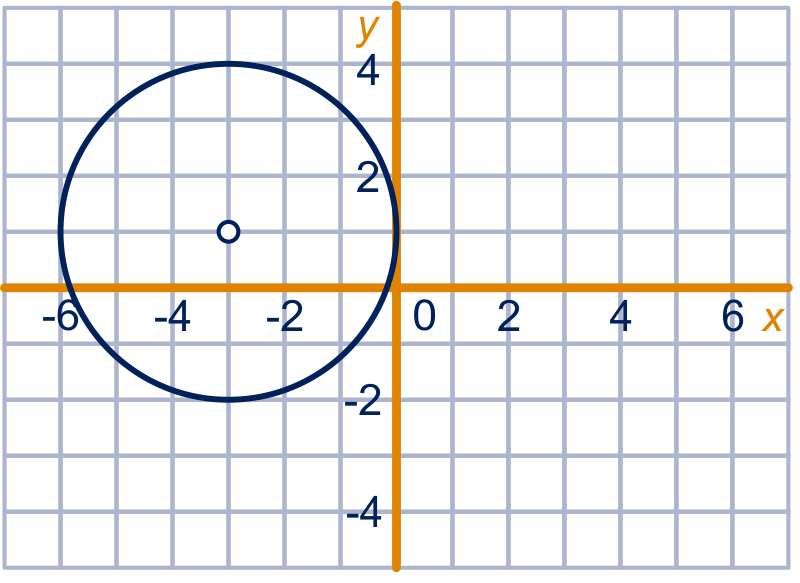
figuur bij opgave 34a
|
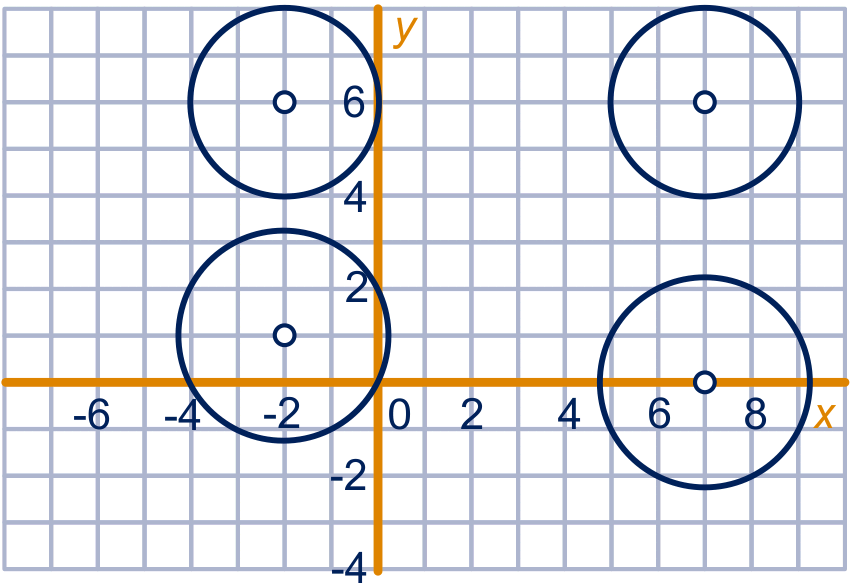
figuur bij opgave 36
|
De afstand van tot
is .
Kwadrateren geeft het gewenste resultaat.
en
en
en
en
Zie de figuur rechts bij opgave 34.
Het middelpunt van de cirkel ligt evenver van als van .
De richtingscoëfficiënt van lijn is , dus de richtingscoëfficiënt van de middelloodlijn van is . Het midden ligt op de middelloodlijn, dus een vergelijking is: .
snijden met geeft het middelpunt van de cirkel: .
De straal van de cirkel is de afstand van
tot bijvoorbeeld , dus
.
Een vergelijking van de cirkel is:
.
Van naar moet je eenheid naar links en naar boven. Om van naar te komen, moet je hetzelfde doen, dus .
Het middelpunt is het snijpunt van de diagonalen, oftewel met midden van de rechthoek,
dat is .
Een vergelijking van de cirkel is:
.
Voor invullen in
geeft:
.
De snijpunten zijn
en .
Noem de projectie van op de -as , en één van de snijpunten , dan driehoek rechthoekig met schuine zijde en rechthoekszijde . De gevraagde afstand is .
Pas de cosinusregel toe: , dus .
Pas weer de cosinusregel toe: , dus .
, vereenvoudigen geeft het resultaat.
,
dus middelpunt en straal .
, dus middelpunt en straal .
, dus middelpunt en straal .
-
Je krijgt dus de lijn met vergelijking
en de lijn met vergelijking .
, je krijgt de lijn en de lijn .
De cirkel heeft middelpunt en straal .
Punten met gehele coördinaten die op afstand van
liggen zijn:
enzovoort,
dus roosterpunten die op afstand van
liggen zijn bijvoorbeeld:
,
en
en
is
de afstand van tot .
is de afstand van
tot .
kwadrateren geeft:
.
Klopt!
, dus middelpunt en straal .
De afstanden van tot alledrie de hoekpunten zijn , dat is ook de straal van de cirkel.
Driehoek krijg je door driehoek ten opzichte van met te vermenigvuldigen. Van naar ga je eenheden naar boven en eenheden naar rechts. Dus om in te komen, moet je eenheid naar rechts en naar boven vanuit , dus .
De straal is .