De afstand van twee punten

We kijken nog eens precies naar de afstand van twee punten in het $O x y$ -vlak.

Door een horizontale en verticale lijn door het punt $K (1,2)$ wordt het platte vlak in vier delen verdeeld, rechtsboven, linksboven, linksonder en rechtsonder, zie figuur 1 hieronder.
Als een punt $(x, y)$ rechtsboven $K$ ligt, dan $x > 1$ en $y > 2$ .

Neem over en vul aan:
Als een punt

linksboven $K$ ligt, dan	$x \dots$ en $y \dots$ ,
linksonder $K$ ligt, dan	$x \dots$ en $y \dots$ ,
rechtsonder $K$ ligt, dan	$x \dots$ en $y \dots$ .

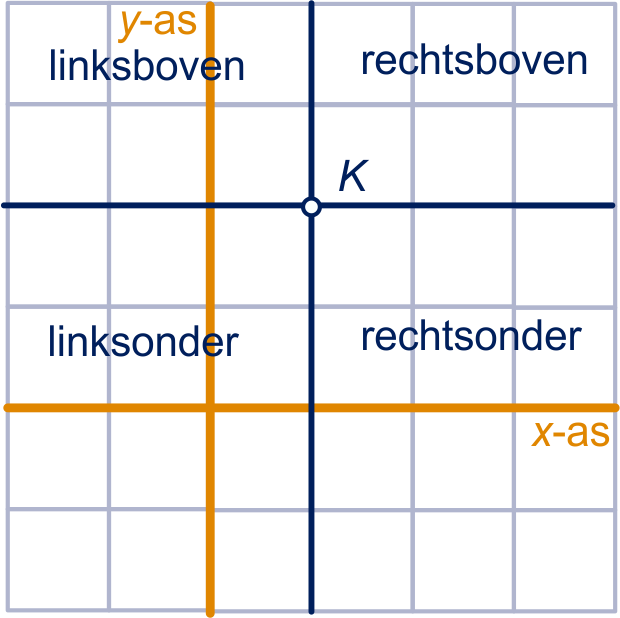
figuur 1

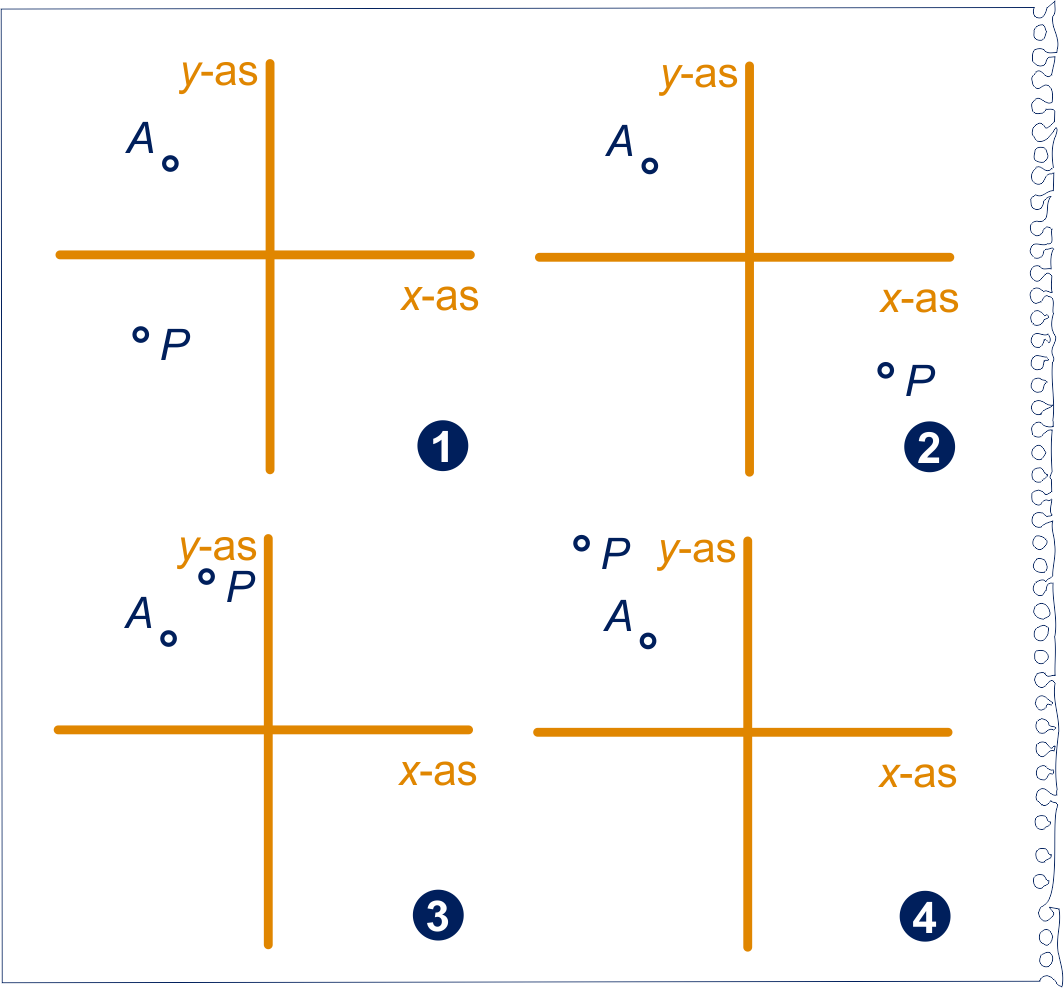
figuur 2

Figuur 2 bestaat uit vier plaatjes met de punten $A (a, b)$ en $P (p, q)$ .
$P$ ligt steeds anders ten opzichte van $A$ .
We onderscheiden vier mogelijkheden:

a: $p > a$ en $q > b$ ,	b: $p < a$ en $q > b$ ,
c: $p > a$ en $q < b$ ,	d: $p < a$ en $q < b$ .

Welk plaatje hoort bij welke mogelijkheid?

figuur 3

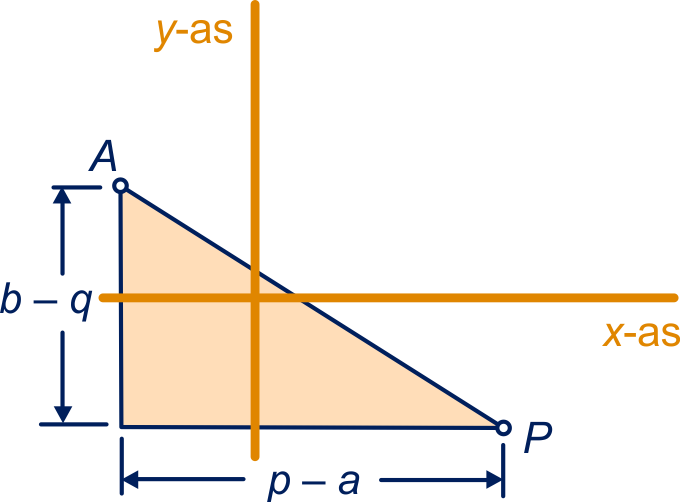
Om de afstand van $A$ tot $P$ te berekenen, kun je in figuur 3 een rechthoekige driehoek tekenen met rechthoekszijden $p - a$ en $b - q$ .
De afstand van $A$ tot $P$ is: $\sqrt{{(p - a)}^{2} + {(b - q)}^{2}}$ .

Waarom is dit hetzelfde als: $\sqrt{{(a - p)}^{2} + {(b - q)}^{2}}$ ?

Zo kun je in alle vier de gevallen het volgende nagaan.

De afstand van $A (a, b)$ tot is $P (p, q)$ is: $\sqrt{{(a - p)}^{2} + {(b - q)}^{2}}$ .

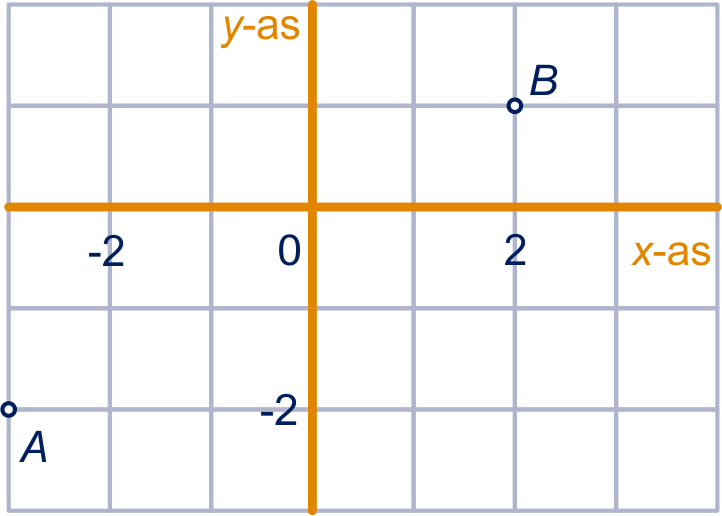
Gegeven zijn de punten $A (‐3,‐2)$ en $B (2,1)$ .

Bereken exact $A B$ .

Bereken exact de afstand van de punten $C (100, ‐3)$ en $D (‐2,70)$ .

Op de lijn $y = x$ liggen twee punten die afstand $2 \sqrt{13}$ tot het punt $(1,3)$ hebben.

Noem de eerste coördinaat van zo'n punt $a$ en stel een vergelijking in $a$ op.
Bereken hiermee $a$ exact.

Op de lijn $y = ‐ x$ liggen punten die afstand $2 \sqrt{34}$ tot $(1,3)$ hebben.

Bereken de coördinaten van deze punten exact.

In het plaatje staat driehoek $A B C$ met $A (‐2,‐3)$ , $B (4,0)$ en $C (0,3)$

Bereken exact de zijden van de driehoek.

Bereken exact de lengte van de hoogtelijn uit $C$ van de driehoek.

(hint)

Snijd de lijn door $C$ loodrecht op lijn $A B$ met lijn $A B$ .

Bereken de oppervlakte van driehoek $A B C$ exact.

Je kunt je antwoord op het vorige onderdeel als volgt controleren.
Denk een vierkant om driehoek $A B C$ , met hoekpunten $A$ , $P (4,‐3)$ , $Q (4,3)$ en $R (‐2,3)$ .
Bereken nu de oppervlakte van de driehoeken $A B P$ , $B Q C$ en $A R C$ .
De oppervlakte van driehoek $A B C$ is met de oppervlakte van die drie driehoeken samen $36$ .

Voer die controle uit.

Bereken hoek $C A B$ exact.

(hint)

Gebruik de cosinusregel of de oppervlakteregel uit hoofdstuk 2.

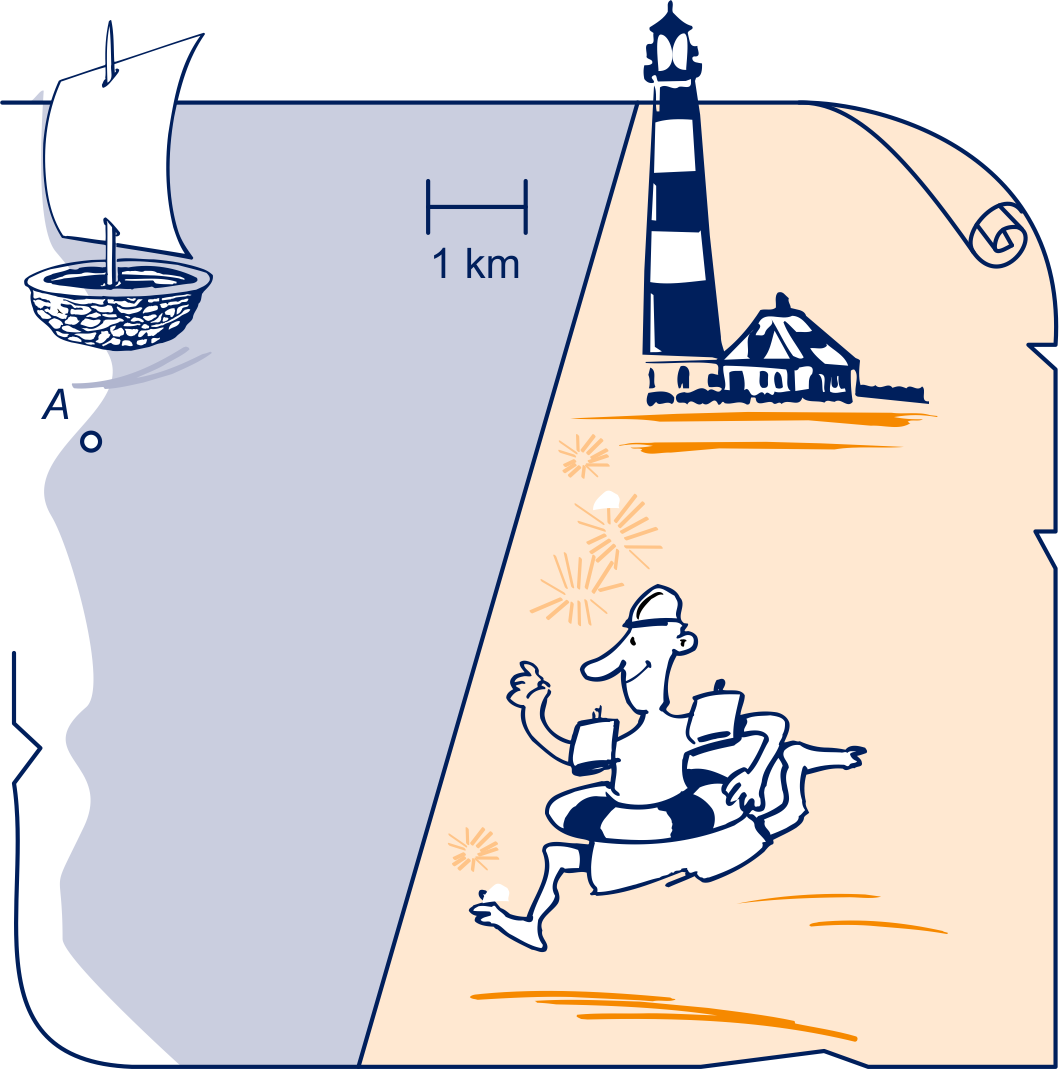
Voor de Nederlandse kust bevindt zich een schip in $A$ .

Hoe ver is het schip volgens jou van de kust verwijderd?
Meet dat in de figuur op het werkblad.
Geef aan hoe je je antwoord gevonden hebt.

De afstand van een punt tot een gebied is de lengte van het kortste verbindingslijnstuk van dat punt met het gebied.

Opmerking:

Er is niet altijd een kortste verbindingslijnstuk van een punt met een gebied.
Neem het gebied $G$ (blauw) bestaande uit alle punten met tweede coördinaat groter dan $1$ . Er is geen kortste verbindingslijnstuk, de stippellijn $y = 1$ hoort namelijk niet bij $G$ .

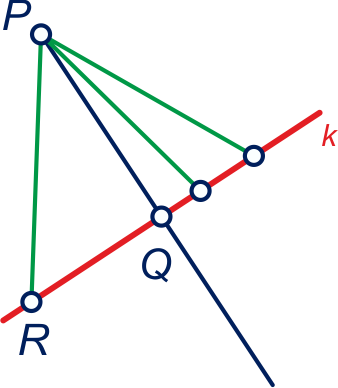
In het plaatje liggen $Q$ en $R$ op lijn $k$ en $P$ niet.
$Q$ is de projectie van $P$ op $k$ , dus hoek $P Q R$ is recht.
Neem aan: $P Q = 5$ en $Q R = 3$ .

Bereken $P R$ exact.

Waarom geldt voor elk punt $X \neq Q$ op lijn $k$ dat $P X > P Q$ ?

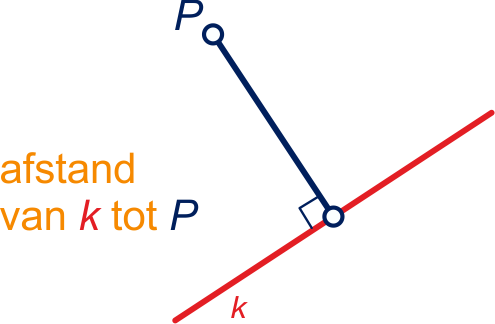
De afstand van een punt $P$ tot een lijn $k$ is de lengte van het loodrechte verbindingslijnstuk van $P$ met lijn $k$ .

In de figuur is de lengte van het blauwe lijnstuk de afstand van $P$ tot $k$ .

Hiernaast is driehoek $A B C$ getekend met $A (‐3,1)$ , $B (1,1)$ en $C (1,4)$ .
In driehoek $A B C$ ligt $M (0,2)$ .

Wat is de afstand van $M$ tot de zijde $A B$ ? En tot de zijde $B C$ ? (Hier valt niet veel aan te rekenen.)

Bereken de oppervlakte van driehoek $A M B$ , van driehoek $B M C$ en van driehoek $A B C$ exact.

Met behulp van het vorige onderdeel kun je de afstand van $M$ tot zijde $A C$ exact berekenen.

Bereken deze afstand.

$M$ ligt even ver van de zijden van driehoek $A B C$ . Het is het middelpunt van de ingeschreven cirkel van driehoek $A B C$ , dat is de cirkel die de zijden van de driehoek raakt.

Neem driehoek $A B C$ over op roosterpapier en teken de daarin de ingeschreven cirkel.

De loodrechte projectie van $M$ op zijde $A B$ noemen we $P$ en en de loodrechte projectie van $M$ op zijde $A C$ noemen we $Q$ .

Waarom passen de driehoeken $M A P$ en $M A Q$ precies op elkaar (zijn congruent)?

Dus lijn $A M$ deelt hoek $B A C$ in twee gelijke stukken, is dus de bissectrice (deellijn) van hoek $A$ .

Opmerking:

Het punt $M$ in de vorige opgave is het snijpunt van de bissectrices (deellijnen) van driehoek $A B C$ .
In het algemeen geldt dat het snijpunt van de bissectrices in een driehoek het middelpunt van de ingeschreven cirkel van die driehoek is.
De ingeschreven cirkel van een driehoek is de cirkel die de zijden van de driehoek raakt.

$O A B$ is een gelijkbenige rechthoekige driehoek met $O (0,0)$ , $A$ op de $x$ -as en $B$ op de $y$ -as.
Het punt $P (3,3)$ heeft afstand $2$ tot driehoek $O A B$ .

Bereken $O A$ exact. (Twee mogelijkheden.)
NB. Met driehoek $O A B$ wordt bedoeld de drie lijnstukken die de driehoek vormen, dus zonder het inwendige.

Gegeven is de cirkel met middelpunt $M (2,0)$ en straal $\sqrt{10}$ en het punt $P (8,2)$ .

Bereken exact de afstand van $P$ tot de cirkel.

Gegeven zijn de punten $O (0,0)$ , $A (4,0)$ , $B (1,2)$ en $C (6,2)$ .

Bereken exact de oppervlakte van driehoek $O A B$ en ook van driehoek $O A C$ .

Op de lijn $y = \frac{1}{2} x - 10$ ligt een punt $P$ zó, dat de oppervlakte van driehoek $O A P = 4$ .

Bereken de coördinaten van $P$ exact.
(Twee mogelijkheden.)