
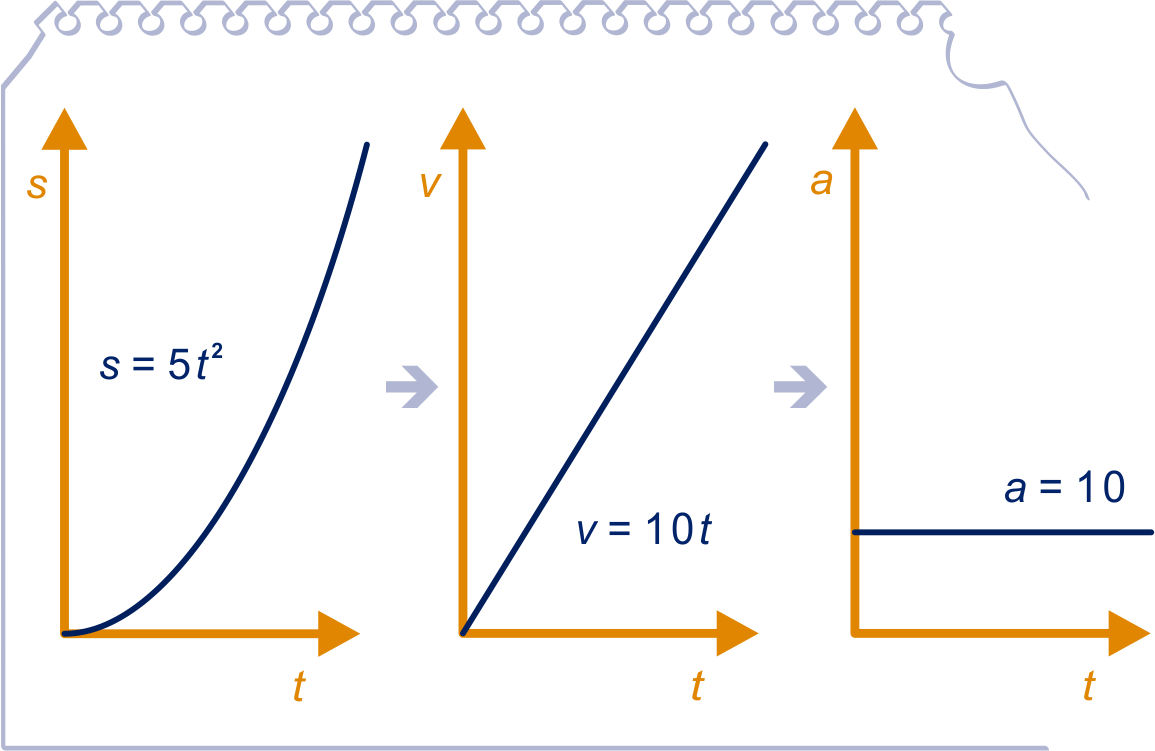
Bij een vrije val op aarde geldt bij benadering: .
Hierin is de valweg in meters en is
de valtijd in seconden.
Als je differentieert, krijg je de snelheid
(in m/s):
.
Als je differentieert, krijg je de versnelling
(in m/s²):
.
Opmerkingen
-
In de natuurkunde zijn de letters , en gebruikelijk.
Zij zijn de beginletters van de Latijnse woorden spatium (= ruimte, afstand), velocitas (= snelheid) en acceleratio (= versnelling). -
Je krijgt door twee keer te differentiëren: .
In plaats hiervan schrijven we ook wel: . -
Bij de vrije val is beginsnelheid genomen.
-
Bij de vrije val ziet men af van luchtwrijving.
De vrije val op de maan wordt (bij benadering) beschreven door de formule:
.
Hoe groot is de valversnelling op de maan?
Op de planeet Mars is de valversnelling m/s².
Geef een formule voor de valweg als functie van de valtijd op Mars.
Bereken de tweede afgeleide van de volgende functies.
Twee sportauto's A en B rijden een rally over een zeer afwisselend parcours. Hieronder is een gedeelte van hun race in beeld gebracht.
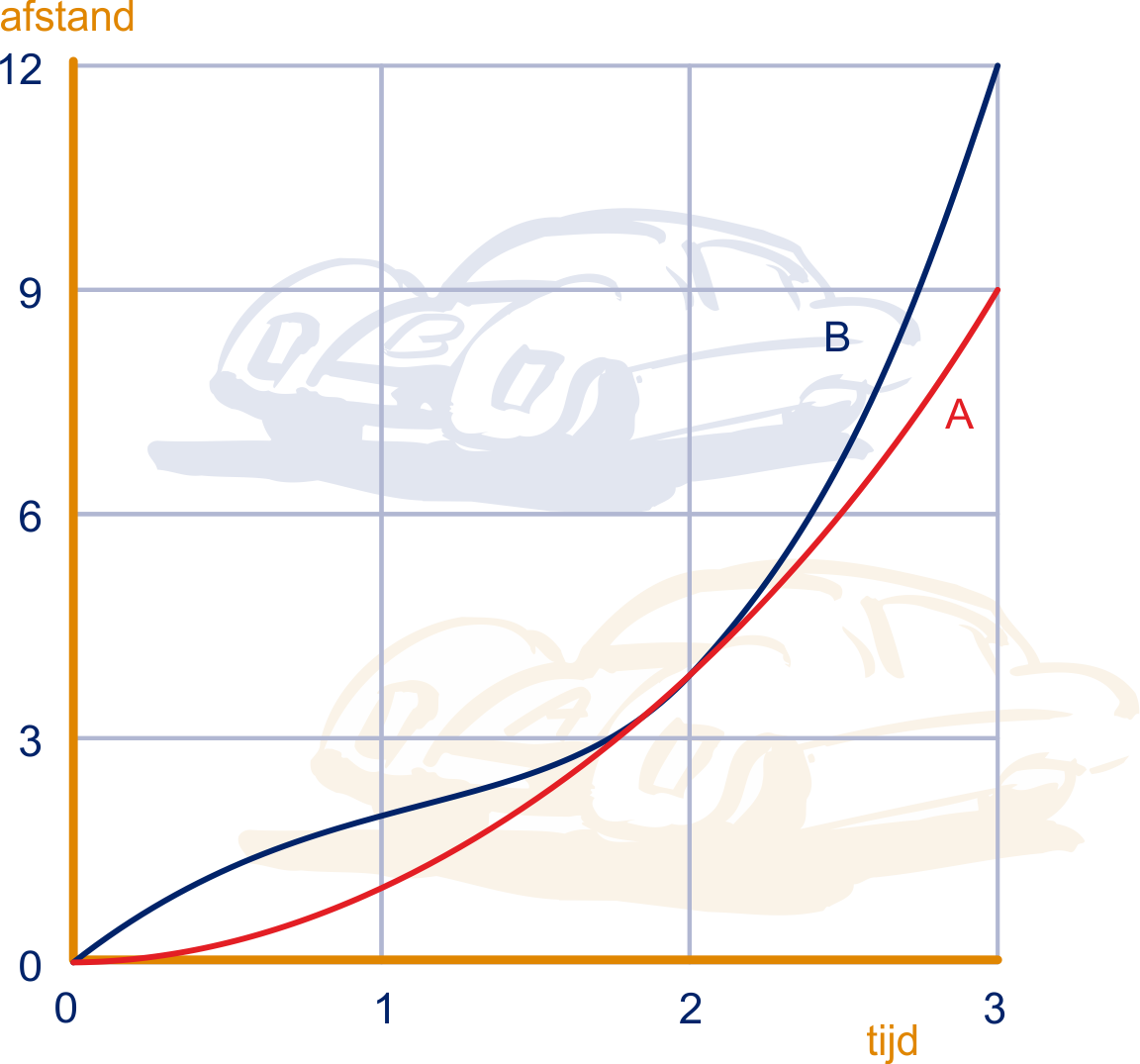
Op de horizontale as is de tijd (in minuten) uitgezet, op de verticale as de afstand vanaf een bevoorradingspost (in eenheden van meter. Op het moment wordt A, die zojuist bijgetankt heeft, ingehaald door B. Voor tijdstippen tussen en wordt de plaats van A gegeven door en de plaats van B door .
Druk de snelheiden en uit in .
Bereken op welke tijdstippen tussen en de auto's precies even hard reden.
Geef een kort verslag van wat er zich afspeelde rond het tijdstip .
Wat is de versnelling van A gedurende het tijdsinterval ?
Teken op de GR de grafiek van de snelheid van B.
Bereken algebraïsch het tijdstip in de periode
waarop de snelheid van B het laagst was.
Hoe groot was de versnelling op dat tijdstip?
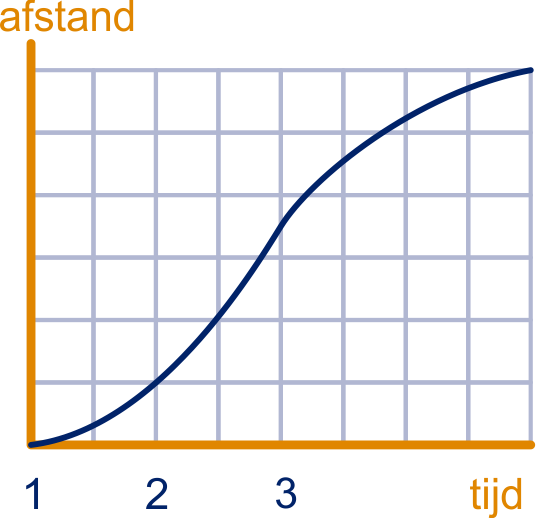
Hiernaast staat de tijd-afstand-grafiek van een stukje autorit.
Wanneer reed de auto het hardst?
Wanneer is de versnelling positief, wanneer negatief en wanneer nul?
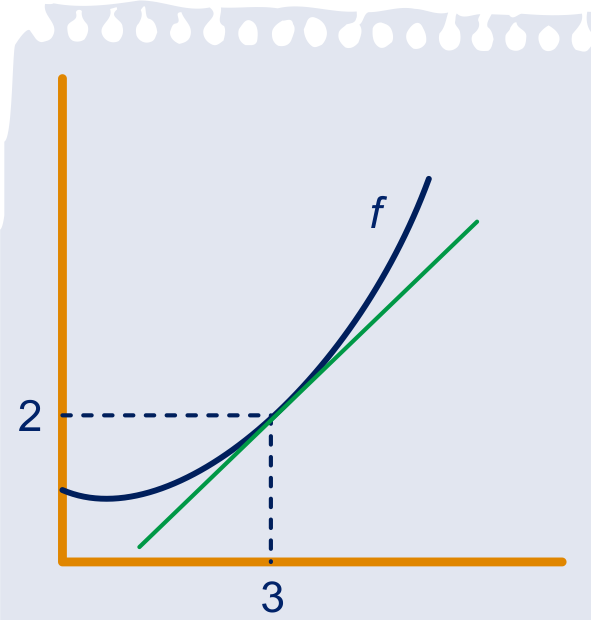
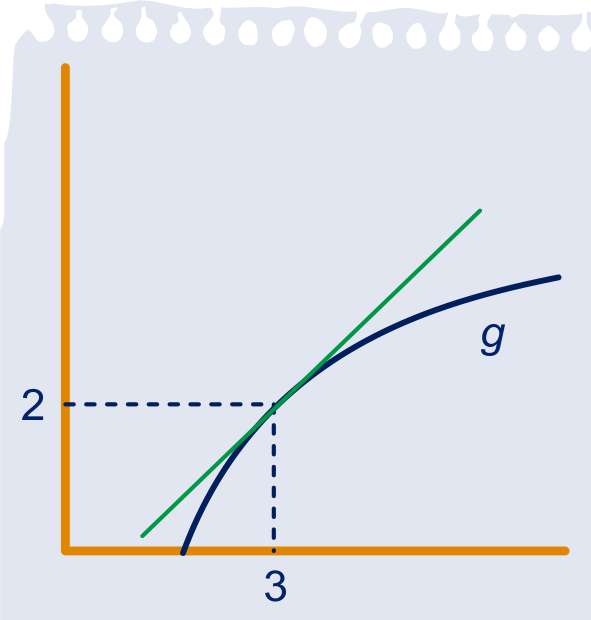
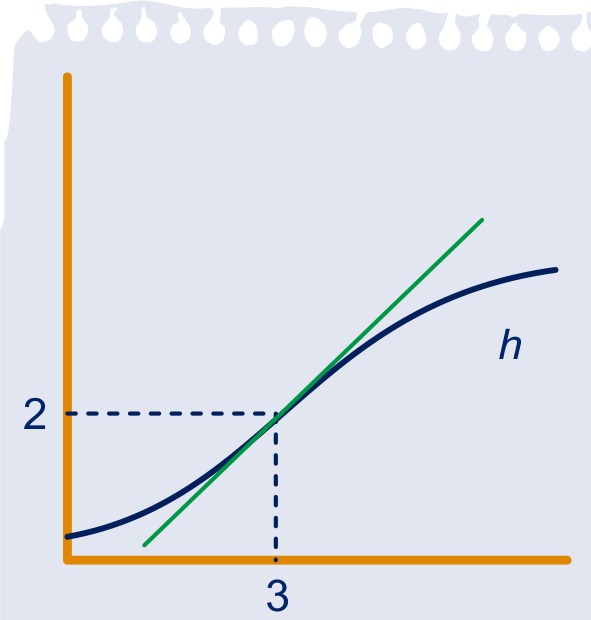
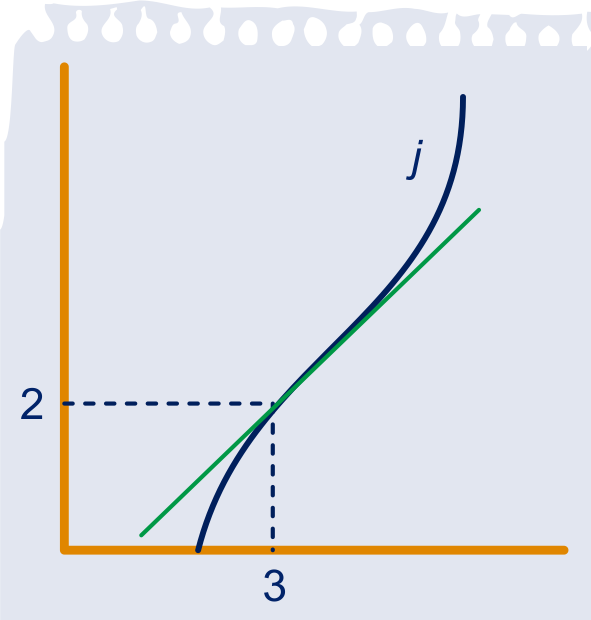
Hieronder staan de grafieken van de functies ,
, en
.
Alle vier de functies nemen in
de waarde aan.
De afgeleide is voor alle vier de functies in
gelijk aan .
Hoe groot de tweede afgeleide is in
is niet zo eenvoudig te zeggen.
,
|
,
|
,
|
,
|
Zeg in elk van de vier gevallen of de tweede afgeleide in positief, negatief of nul is. Licht toe.
