Gegeven is de functie .
Bereken algebraïsch voor welke geldt:
.
Voor welke geldt:
?
Voor welke geldt:
?
In welk punt is de raaklijn aan de grafiek van horizontaal?
Op welk -interval is stijgend?
Op welk -interval is dalend?
Controleer je antwoorden met de grafiek op de GR.
Aan de afgeleide van een functie kun je zien of de functie daalt of stijgt.
Daar waar de afgeleide (de helling) positief is, stijgt de functie; daar waar de afgeleide negatief is, daalt de functie.
Dat is met "" en "" aangegeven in onderstaand plaatje.

Gegeven is de functie .
Bereken algebraïsch voor welke geldt:
.
Voor welke geldt:
?
Voor welke geldt:
?
In welk punt is de raaklijn aan de grafiek van horizontaal?
Op welk -interval is stijgend?
Op welk -interval is dalend?
Controleer je antwoorden met de grafiek op de GR.
In de toppen van de grafiek van een functie is de afgeleide .
De grafiek is stijgend als de afgeleide positief is.
De grafiek is dalend als de afgeleide negatief is.
In formuletaal:
In de toppen van de grafiek van een functie geldt
.
De grafiek is stijgend als .
De grafiek is dalend als .
Hieronder staan de grafieken van drie derdegraadsfuncties: , en .
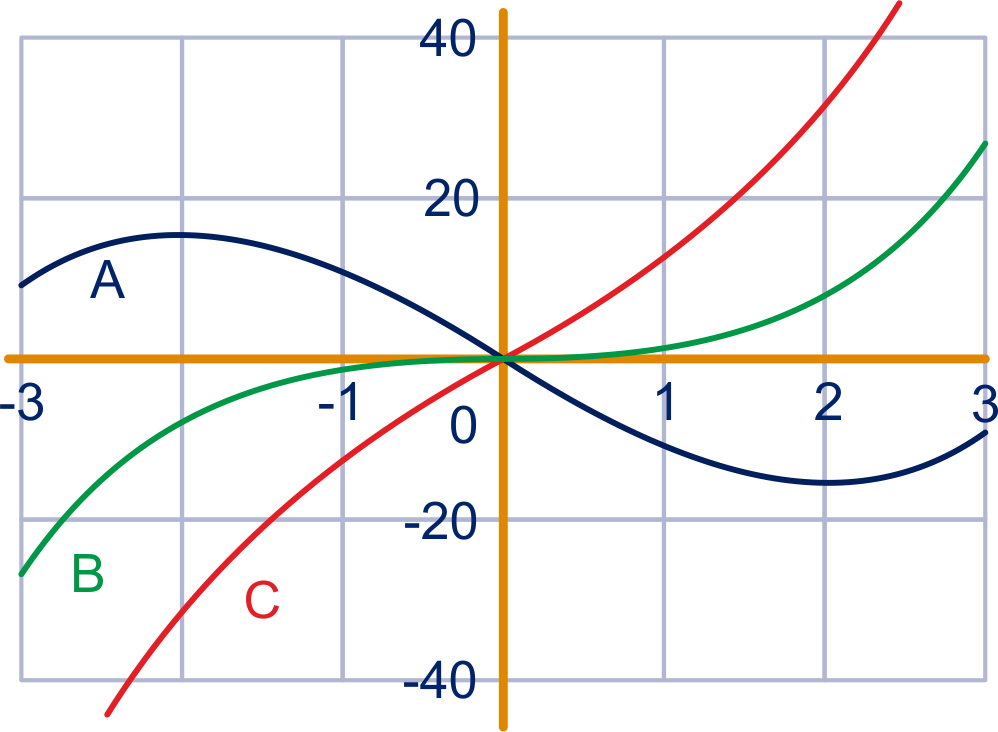
Bereken de afgeleide functies , en .
Leg uit hoe je aan kunt zien dat de functie overal stijgend is.
Leg uit hoe je aan kunt zien dat de grafiek van dalend is op het -interval .
Weet je nu welke van de drie getekende grafieken de grafiek van is? En welke de grafiek van is?
Bereken algebraïsch de coördinaten van de twee toppen van de grafiek van .
Ga na dat de helling van de grafiek tussen deze punten negatief is.
Op welk -interval is dalend?
Op welke -intervallen is stijgend?
Controleer je antwoorden met de grafiek op de GR.
In de vorige onderdelen heb je al gezien dat de hellingfunctie wordt gegeven door:
.
Schrijf deze formule met kwadraatafsplitsen in de vorm .
Leg uit hoe je aan deze laatste formule kunt zien dat de helling het kleinst is als .
Waar heeft de grafiek van afnemende/toenemende daling/stijging? Onderscheid vier -intervallen.
Hieronder is een stukje van het parcours voor motorwegraces getekend. Een coureur rijdt vaak met zijn motor scheef over het wegdek; vooral in de bochten is dat spectaculair.
Waarom houdt hij zijn motor niet gewoon verticaal op het wegdek?

De motorcoureur rijdt in de richting van de pijl.
Waar zal hij (meer of minder) naar rechts overhellen, en waar naar links?
Op één plek van dit stukje parcours staat de motor precies verticaal. Welke plek is dat?
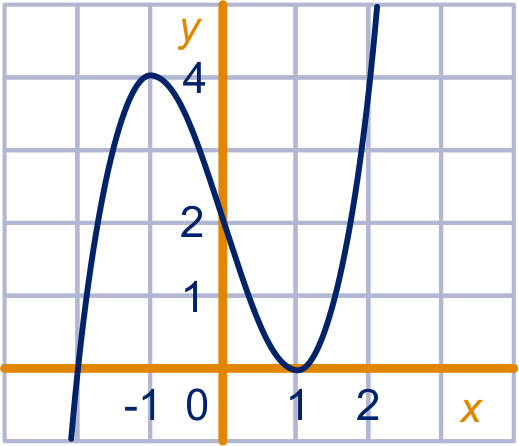
Hiernaast staat de grafiek van
.
We volgen de grafiek van links naar rechts.
De grafiek is eerst naar rechs gekromd en later naar links.
Daartussen in zit het "omslagpunt"; dat noemen we het
buigpunt
van de grafiek.
Je kunt ook zeggen dat vóór het buigpunt de grafiek van onderen gezien hol is en na het buigpunt van boven gezien hol is.
De raaklijn in het buigpunt heet
buigraaklijn.
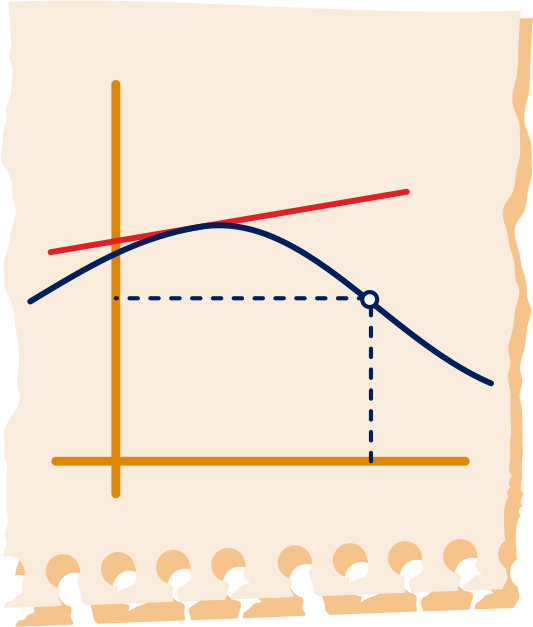
Bekijk de grafiek hiernaast. In punten op de grafiek vóór het buigpunt is de kromming naar rechts. Daar ligt de raaklijn boven de grafiek.
Hoe zit dat in punten op de grafiek ná het buigpunt?
Hoe zit dat in het buigpunt zelf?
In een buigpunt van een grafiek is de helling maximaal of minimaal.
Hieronder staat een grafiek.
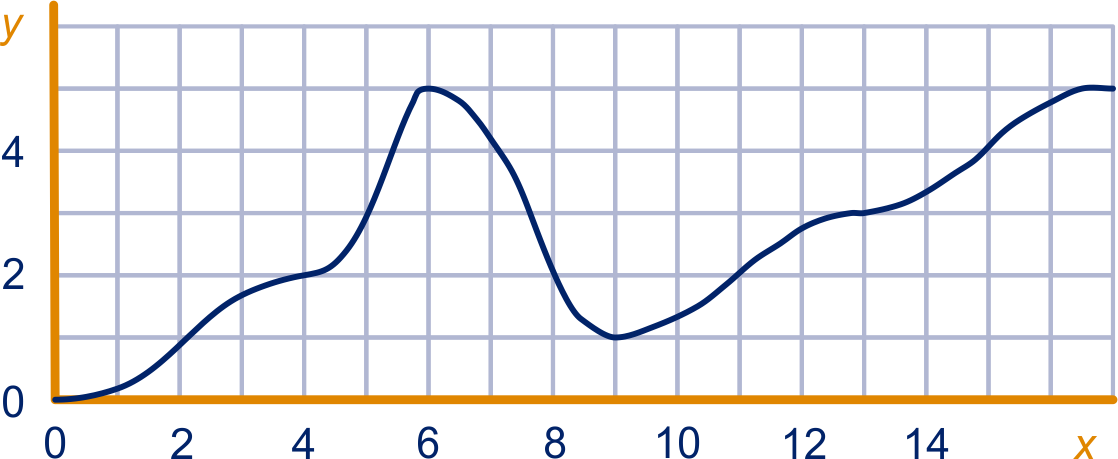
Lees zo nauwkeurig mogelijk de coördinaten van alle buigpunten af.
Geef de richtingscoëfficiënten van de buigraaklijnen (zo goed mogelijk aflezen).
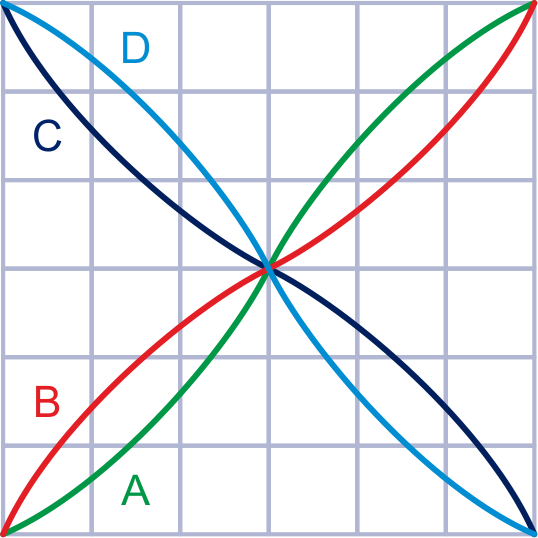
Hiernaast staan de grafieken (A t/m D) getekend van vier functies met hetzelfde buigpunt.
Geef voor elke grafiek aan of in het buigpunt de helling daar maximaal of minimaal is.
Bereken exact de coördinaten van de punten waar de raaklijn horizontaal is.
Schrijf met kwadraatafsplitsen de formule van in de vorm .
Leg uit hoe je aan de formule van vraag b kunt zien dat de grafiek van een buigpunt heeft. Is de helling in het buigpunt maximaal of minimaal? Wat is deze maximale of minimale waarde?
Bereken de exacte coördinaten van het buigpunt en geef een formule van de buigraaklijn.
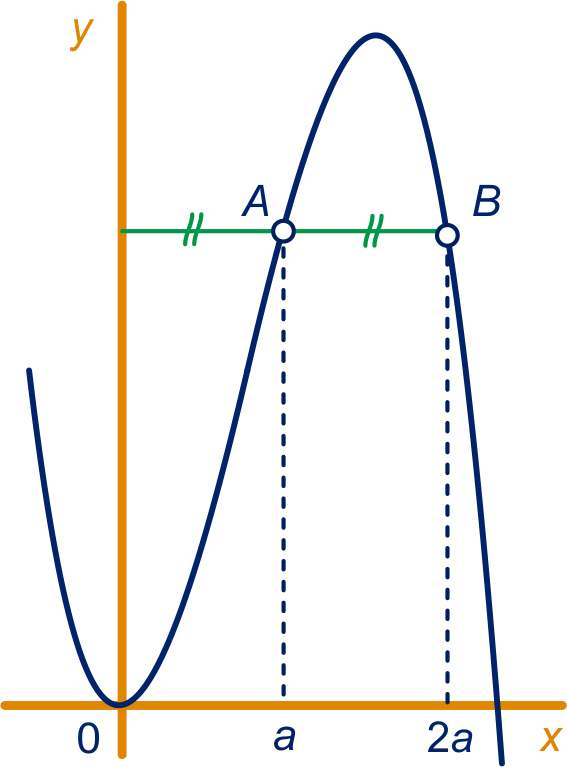
![]() Op de grafiek van liggen twee punten en
op gelijke hoogte aan dezelfde kant van de -as.
Punt ligt dubbel zo ver van de
-as af als punt .
Op de grafiek van liggen twee punten en
op gelijke hoogte aan dezelfde kant van de -as.
Punt ligt dubbel zo ver van de
-as af als punt .
De -coördinaat van
punt noemen we .
Dan is de -coördinaat van
punt gelijk aan
.
Bereken de exacte waarde van .
Bij vierdegraadsfuncties is er nog meer variatie dan bij derdegraadsfuncties. Dat laten we zien aan de hand van , , en . Bij elk van deze functies is een tabel gemaakt.
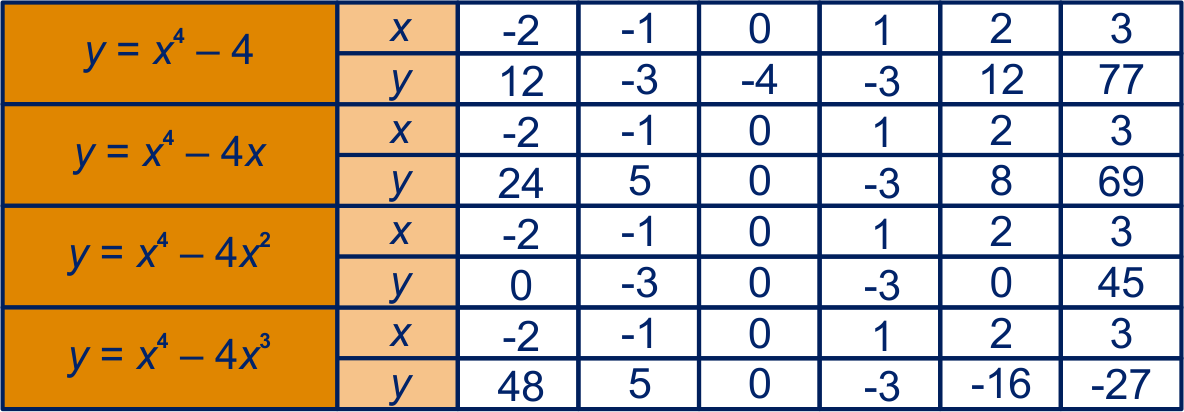
Bekijk de tabel van . Het lijkt er in de tabel op dat de kleinste -waarde is: het minimum (of minimale waarde) van de functie.
Hoe kun je direct aan de formule zien dat dat inderdaad zo is?
Wat weet je van de raaklijn in het punt ?
Je kunt het minimum van de functie ook berekenen met behulp van de afgeleide.
Doe dit.
Schets de grafiek van . Controleer je tekening op de GR.
Bereken exact de nulpunten van de functie; dat zijn de waarden van waarvoor .
De kleinste -waarde die een functie
(op een -interval) aanneemt, is het
minimum van (op dat interval).
De grootste -waarde die een functie
(op een -interval) aanneemt, is het
maximum van (op dat interval).
Bekijk de tabel van . Het lijkt er in de tabel op dat het minimum van de functie is. Bij deze functie kun je niet direct aan de formule zien of dat waar is.
Als het minimum is, moet de raaklijn in het betreffende punt van de grafiek horizontaal zijn.
Controleer met een berekening of dat het geval is.
Is inderdaad het minimum?
Schets de grafiek van . Controleer je tekening met de GR.
Onder welke hoek snijdt de grafiek de -as in het punt ?
Bekijk de tabel van . Het lijkt er in de tabel op dat ook nu het minimum van de functie is.
Schijn bedriegt. Laat met een berekening zien dat niet het minimum kan zijn.
Bereken algebraïsch het minimum van de functie.
Schets de grafiek van . Controleer je tekening op de GR.
Bekijk de tabel van .
Toon met een berekening aan dat het minimum is van de functie.
Teken de grafiek van deze functie op de GR. Ga na dat er twee punten zijn waar de raaklijn horizontaal is.
In een buigpunt van de grafiek van een functie
bij
is de helling maximaal of minimaal. Dat betekent dat de afgeleide van de hellingfunctie
bij helling nul heeft.
Ofwel: er moet dan gelden ,
ofwel in handigere notatie:
.
We kunnen de coördinaten van een buigpunt dus berekenen door de hellingfunctie
nogmaals te differentiëren en gelijk aan nul te stellen.
De functie heet de
tweede afgeleide
van de functie .
Let op! Er geldt wél: buigpunt bij
.
Maar niet per se geldt ook het omgekeerde: het kan zijn dat voor een bepaalde waarde van geldt dat
, maar dat er toch geen buigpunt is bij
.
We zullen in de volgende opgave zo'n geval tegenkomen.
Lees uit de grafieken van de vier functies ,
,
en
af hoeveel buigpunten hij heeft.
Bereken de tweede afgeleide
van
en los op .
Is er een buigpunt bij de gevonden waarde van ?
Bereken voor de andere drie functies met de tweede afgeleide de exacte -coördinaten van de buigpunten.
Van de vier functies zijn de eerste en de derde symmetrisch ten opzichte van de -as.
Leg uit hoe je dat (zonder berekening) aan de formule kunt zien.
Hieronder staat de grafiek van de vijfdegraadsfunctie
.
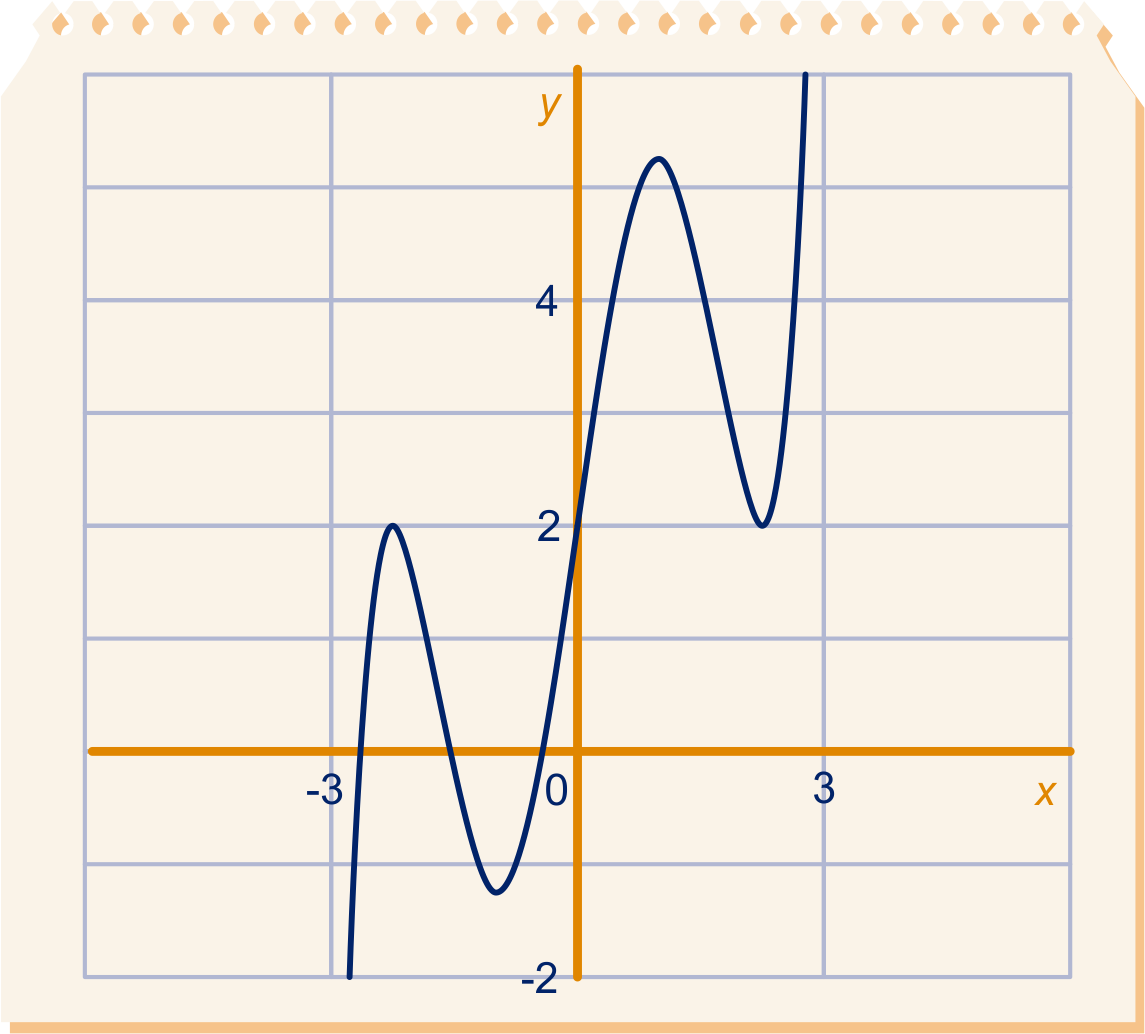
De grafiek heeft vier punten met een horizontale raaklijn.
Bereken exact de -coördinaten van deze punten.
Hoeveel buigpunten heeft de grafiek?
Een van de buigpunten is .
Stel langs algebraïsche weg een vergelijking op van de buigraaklijn in dat punt.
