; als ; als
Raaklijn horizontaal in ; Stijgend op ; Dalend op
-
;
als ;
als
Raaklijn horizontaal in
;
Stijgend op ;
Dalend op .
-
, en
is voor elke waarde van positief, want een kwadraat is groter of gelijk aan , dus is ook groter of gelijk aan , dus is groter of gelijk aan (dus groter of gelijk aan ).
Als , dan , dus , dus .
Grafiek A is van functie ; grafiek C is van functie .
of ;
Toppen
en .
Als
dan
en ,
dus .
Dalend op .
Stijgend op en op .
-
is een dalparabool met top , dus als is de uitkomst (de helling) minimaal, namelijk .
Op :
afnemende stijging;
op :
toenemende daling;
op :
afnemende daling;
op :
toenemende stijging.
Omdat hij anders uit de bocht vliegt.
Voor de bocht hangt hij naar rechts, na de bocht naar links.
Halverwege de bocht.
Daar is de kromming naar links; de raaklijn ligt dan onder de grafiek.
Daar wisselt de raaklijn van kant ten opzichte van de grafiek.
, , , , , ,
, , , , , ,
A: maximaal; B: minimaal; C: maximaal; D: minimaal
of ;
Punten
en .
De grafiek van de hellingfunctie , is een bergparabool met top , dus bij is de helling maximaal .
Buigpunt: ,
dus ;
Coördinaten buigpunt invullen in
:
;
Buigraaklijn:
... of
voor elke , dus voor alle .
De raaklijn is horizontaal en heeft richtingscoëfficiënt .
; het minimum is
Zie figuur bij opgave 89b.
of
;
, dus horizontale raaklijn.
Ja, is het minimum.
Zie figuur bij opgave 89b.
(Let op: de hoek tussen twee lijnen is altijd scherp! Een hellingshoek kan wél stomp zijn.)
;
, dus geen horizontale raaklijn en dus geen minimum.
of
of
of ;
,
,
dus is het minimum.
Zie figuur bij opgave 89b.
of ;
en
, dus is het minimum.
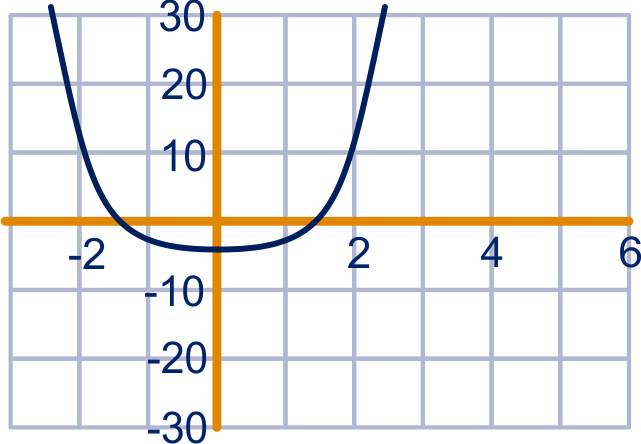
opgave 86
|
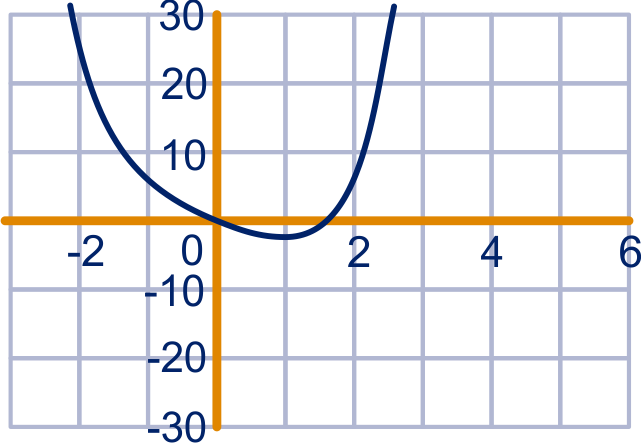
opgave 87
|
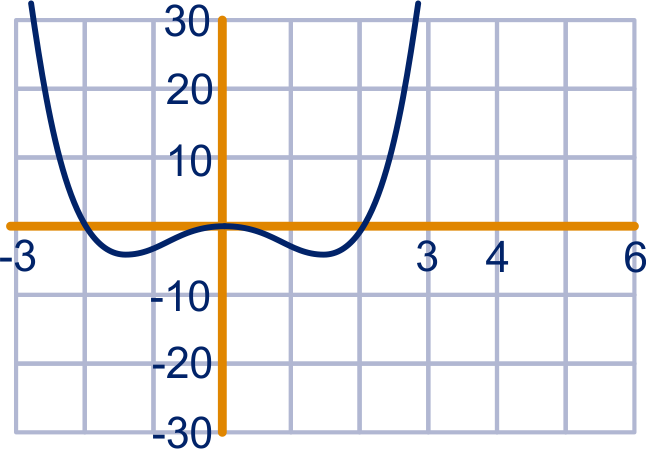
opgave 88
|
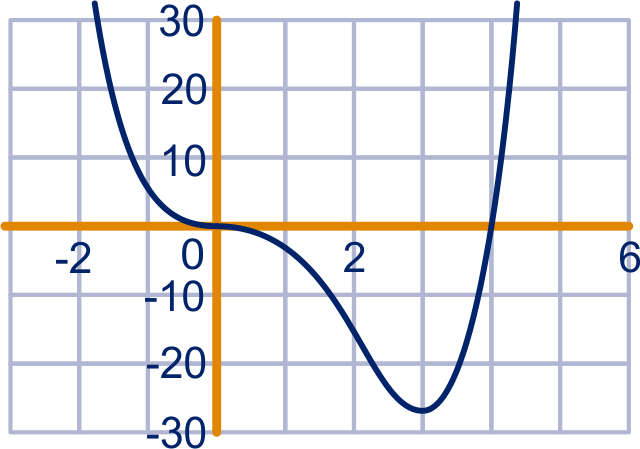
opgave 89
|
: buigpunten;
: buigpunten;
: buigpunten;
: buigpunten.
;
Nee, er is géén buigpunt bij !
Bij : geen buigpunten;
Bij :
of ;
Bij :
of
en , dus voor tegengestelde waarden van geeft de functie dezelfde uitkomst.
(noem :) of of of of of
Drie buigpunten.
punt
invullen in
;
Raaklijn: .
