Als je op tijdstip $t$ in $(a,b)$ bent, dan ben je op tijdstip $\mathrm{‐}t$ in $(b,a)$.

De snelheidsvector is $\left(\begin{array}{c}2t-2\\ 2t+2\end{array}\right)$. De raaklijn is horizontaal als de verticale component $0$ is en de horizontale niet. Dat is als $t=\mathrm{‐}1$, dus in $(\mathrm{3,}\mathrm{‐}1)$.

-

Uit het vorige onderdeel volgt dat het punt bereikt wordt op $t=5$. De snelheidsvector op dat moment is: $\left(\begin{array}{c}8\\ 12\end{array}\right)$, dus de richtingscoëfficiënt van de raaklijn is $1\frac{1}{2}$.
Een vergelijking van de raaklijn is: $y=1\frac{1}{2}x+12\frac{1}{2}$.

$x=\frac{1}{16}{(y-x)}^2-\frac{1}{2}(y-x)$ $\to$ $16x={(y-x)}^2-8(y-x)$ $\to$ ${(y-x)}^2=16x+8(y-x)$ $\to$ ${(x-y)}^2=8(x+y)$

De $x$-as is symmetrie-as van de baan.

$\sqrt{{\left(t^2-4\right)}^2+{\left(2t\right)}^2}=\sqrt{t^4-4t^2+16}$

Dan moet $t^4-4t^2+16={(t^2-2)}^2+12$ minimaal zijn. Dat is zo als $t^2-2=0$, dus $t=\pm \sqrt{2}$. De bijbehorende punten zijn: $(\mathrm{‐}\mathrm{2,2}\sqrt{2})$ en $(\mathrm{‐}\mathrm{2,}\mathrm{‐}2\sqrt{2})$.

De snelheidsvector is $\left(\begin{array}{c}2t\\ 2\end{array}\right)$, in $A$ dus $\left(\begin{array}{c}2\sqrt{2}\\ 2\end{array}\right)$ en $\overrightarrow{OA}=\left(\begin{array}{c}\mathrm{‐2}\\ 2\sqrt{2}\end{array}\right)$. Het inproduct van deze twee vectoren is $\left(\begin{array}{c}2\sqrt{2}\\ 2\end{array}\right)\cdot \left(\begin{array}{c}\mathrm{‐2}\\ 2\sqrt{2}\end{array}\right)=0$.

Een vergelijking van de baan van $P$ is $y=\frac{1}{2}x$. $Q$ komt op die baan als $\frac{1}{4}{t}^2-2\frac{1}{4}=\frac{1}{2}(t+3)\iff t^2-2t-15=0$, dus als $t=\mathrm{‐}3$ of $t=5$.
De snijpunten zijn dus $(\mathrm{0,0})$ en $(\mathrm{8,4})$.

De afstand is:
$\sqrt{{\left(t-3-\left(t+3\right)\right)}^2+{\left(\frac{1}{2}t-1\frac{1}{2}-\left(\frac{1}{4}{t}^2-2\frac{1}{4}\right)\right)}^2}$ $=\sqrt{36+{(\mathrm{‐}\frac{1}{4}{t}^2+\frac{1}{2}t+\frac{3}{4})}^2}$. Deze is minimaal als $\mathrm{‐}\frac{1}{4}{t}^2+\frac{1}{2}t+\frac{3}{4}=0$ is en dat is als $t=\mathrm{‐}1$ of $t=3$. De afstand is dan: $6$.

Dan moet $P$ op bijvoorbeeld $t=\mathrm{‐}3$ in $(\mathrm{0,0})$ zijn.
Bijvoorbeeld: $(x,y)=(t+\mathrm{3,}\frac{1}{2}t+1\frac{1}{2})$.

$t=0$

Het punt is dan al drie keer 'rond' geweest, dus $t=\frac{1}{6}\text{π}+3\cdot 2\text{π}=6\frac{1}{6}\text{π}$.

De snelheidsvector op tijdstip $t$ is: $\left(\begin{array}{l}{\mathrm{1,2}}^t\cdot \ln \left(\mathrm{1,2}\right)\cdot \cos (t)-{\mathrm{1,2}}^t\cdot \sin (t)\hfill \\ {\mathrm{1,2}}^t\cdot \ln \left(\mathrm{1,2}\right)\cdot \sin (t)+{\mathrm{1,2}}^t\cdot \cos (t)\hfill \end{array}\right)$.

De radiële component (langs lijn $OQ$) is ${\mathrm{1,2}}^t\cdot \ln \left(\mathrm{1,2}\right)\cdot \left(\begin{array}{l}\cos (t)\hfill \\ \sin (t)\hfill \end{array}\right)$ en de component daar loodrecht op is: ${\mathrm{1,2}}^t\cdot \left(\begin{array}{l}\mathrm{‐}\sin (t)\hfill \\ \cos (t)\hfill \end{array}\right)$; de eerste heeft lengte ${\mathrm{1,2}}^t\cdot \ln \left(\mathrm{1,2}\right)$ en de tweede ${\mathrm{1,2}}^t$. De verhouding is $\ln \left(\mathrm{1,2}\right)$ voor elke waarde van $t$.

$\left(\begin{array}{l}\mathrm{‐}\sin (t)+\sin (t)+t\cos (t)\\ \cos (t)-\cos (t)+t\sin (t)\end{array}\right)=t\left(\begin{array}{l}\cos (t)\\ \sin (t)\end{array}\right)$

De vector $t\left(\begin{array}{l}\cos (t)\\ \sin (t)\end{array}\right)$ is $t$ keer zo lang als $\left(\begin{array}{l}\cos (t)\\ \sin (t)\end{array}\right)$.

Teken de vector met lengte $PQ$ die evenwijdig met lijn $OQ$ is.

-

Je krijgt een parabool met top $\left(\mathrm{0,5}\right)$ zo te zien.

De projectie van $A$ op lijn $PT$ noemen we $B$, $P=(x,y)$.
Dan $AB=x$, $PB=y-5$ en $BT=5$, dus $x^2=(y-5)\cdot 5$.

$x^2=(y-5)\cdot 5\iff y=\frac{1}{5}{x}^2+5$, dus de top is $(\mathrm{0,5})$.

Dat volgt uit de omgekeerde stelling van Thales, hoek $DOE$ is recht.

-

Zie figuur op de volgende bladzijde.

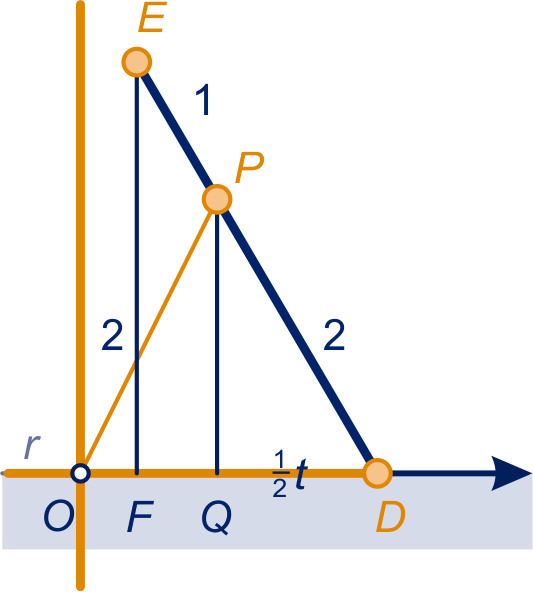
$F$ en $Q$ zijn de projecties van $E$ en $P$ op de $x$-as.
Omdat driehoek $POD$ gelijkbenig is, geldt: $DQ=\frac{1}{2}t$.
Dus $PQ=\sqrt{4-\frac{1}{4}{t}^2}$ en $DF=1\frac{1}{2}\cdot DQ=\frac{3}{4}t$, dus $OF=\frac{1}{4}t$
Verder: $EF=1\frac{1}{2}\cdot PQ=1\frac{1}{2}\cdot \sqrt{4-\frac{1}{4}{t}^2}$ .

$x^2+{\left(\frac{y}{3}\right)}^2=1$

${\left(\frac{1}{4}t\right)}^2+{\left(\frac{1\frac{1}{2}\sqrt{4-\frac{1}{4}{t}^2}}{3}\right)}^2=$
$\frac{1}{16}{t}^2+\frac{2\frac{1}{4}\left(4-\frac{1}{4}{t}^2\right)}{9}=$ $\frac{1}{16}{t}^2+\frac{1}{4}\left(4-\frac{1}{4}{t}^2\right)=1$.

De coördinaten van $B$ zijn $(\mathrm{0,}\sqrt{4-t^2})$, dus $Z=(\frac{1}{3}t,\frac{1}{3}\sqrt{4-t^2})$.

-

$x^2+y^2=\frac{4}{9}$

-

Omdat $\cos (\mathrm{‐}a)=\cos (a)$ voor alle waarden van $a$.

$y(\mathrm{‐}t)=\mathrm{‐}y(t)$

De figuur is symmetrisch in de $x$-as.

Noem die $v$, dan $v^2={(\mathrm{‐}2\sin (t)-2\sin (2t))}^2+{(2\cos (t)-2\cos (2t))}^2$
$=4{\sin }^2(t)+8\sin (t)\cdot \sin (2t)-8\cos (t)\cos (2t)+4{\cos }^2(t)+4{\cos }^2(2t)$
$=8-8\cos (3t)$.

$\cos (3t)=1\iff 3t=k\cdot 2\text{π}\iff t=k\cdot \frac{2}{3}\text{π}$, dus op de tijdstippen $0$, $\frac{2}{3}\text{π}$, $1\frac{1}{3}\text{π}$ en $2\text{π}$.

Voor de antwoorden van de laatste opgave, zie volgende bladzijde.

Boog $AC$ heeft lengte $\frac{1}{4}\cdot 2\text{π}\cdot 10=5\text{π}$. De tijd nodig om die boog te doorlopen is $5\text{π}:\frac{1}{2}\text{π}=10$. Dat is ook de tijd die voor de horizontale lijn nodig is om van $A$ naar $B$ te komen.

figuur 1

figuur 2

figuur 3

-

Noem de hoek $\text{α}$, dan $\text{α}=\mathrm{0,05}\text{π}t$.

Zie figuur 1, $y_S=ST=t$ en $x_S=OT=\frac{t}{\tan \left(\text{α}\right)}=\frac{t}{\tan \left(\mathrm{0,05}\text{π}t\right)}$.

Ja, zie figuur 2.
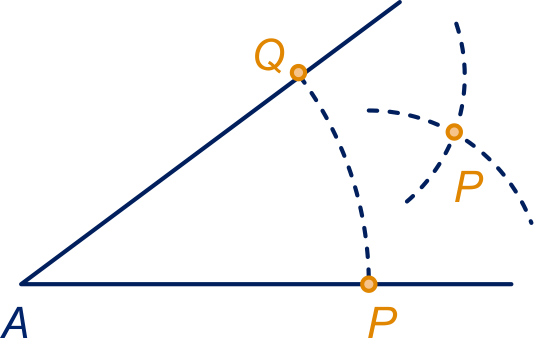
Teken met de passer op de benen de punten $P$ en $Q$ die even ver van het hoekpunt $A$ afliggen. Teken vervolgens met de passer een punt $R$, dat even ver van $P$ als van $Q$ ligt. Lijn $AR$ deelt hoek $A$ in twee gelijke delen.

Zie figuur 3. Leg de hoek met het hoekpunt in $O$ en het ene been langs de $x$-as. Het andere been snijdt de quadratrix in $S$. De projectie van $S$ op de $y$-as noemen we $U$.
Verdeel lijnstuk $OU$ in drie gelijke stukken en teken door de verdeelpunten lijnen evenwijdig aan de $x$-as. Die snijden de quadratrix in twee punten. Door elk van die punten met $O$ te verbinden, deel je de hoek in drie gelijke stukken.

Ja, dat gaat net zo. Dan moet je $OU$ in vijf gelijke stukken verdelen.