Het verband tussen helling en hellingshoek

Er is een verband tussen de helling van een lijn en de hoek die die lijn met de $x$ -as maakt.

Een lijn maakt dezelfde hoek met de $x$ -as als zijn spiegelbeeld in de $x$ -as.

Als $k$ helling $\frac{3}{4}$ heeft, wat is dan de helling van zijn spiegelbeeld in de $x$ -as? En als $k$ richtingscoëfficiënt $m$ heeft?

Een (niet horizontale) lijn $k$ maakt vier hoeken met de $x$ -as. Noem een van de niet-stompe hoeken α.
We spreken af: de hellingshoek van $k$ is $α$ als de helling van $k$ positief is en -α als de helling van $k$ negatief is.

Zo heeft een lijn met helling $1$ een hellingshoek van $45 °$ en een lijn met helling $‐ 1$ een hellingshoek van $‐ 45 °$ .

In het plaatje hiernaast liggen de punten $A$ en $B$ op lijn $k$ . Het verschil tussen de $x$ -coördinaten van $A$ en $B$ is $1$ .

Als $k$ helling $\frac{1}{2}$ heeft, hoe groot is dan het verschil tussen de $y$ -coördinaten?
Bereken in dit geval $∠ C A B$ in graden nauwkeurig.
Hoek $C A B$ is even groot als de hoek van $k$ met de $x$ -as.

We spreken af: als $‐ 90 ° < α < 0 °$ , dan $\tan (α) = ‐ \tan (‐ α)$ .

Ga na dat de rekenmachine ook volgens bovenstaande afspraak werkt.

Geef de exacte waarde van $\tan (‐ 30 °)$ , $\tan (‐ 45 °)$ en $\tan (‐ 60 °)$ .

Geef de richtingscoëfficiënt (helling) van een lijn met hellingshoek $‐ 70 °$ in twee decimalen.

Afspraak

Een (niet horizontale) lijn $k$ maakt vier hoeken met de $x$ -as. Noem een niet-stompe hoek α.
We spreken af: de hellingshoek van $k$ is $α$ als de helling van $k$ positief is en -α als de helling van $k$ negatief is.
Als $‐ 90 ° < α < 0 °$ , dan $\tan (α) = ‐ \tan (‐ α)$ .

Onze afspraken zijn zó gemaakt dat het volgende geldt.

De lijn met hellingshoek $α$ heeft helling $\tan (α)$ .

Opmerking:

De rekenmachine werkt volgens onze afspraak.

Geef in één decimaal nauwkeurig de hellingshoek van de lijn:

$k$ met vv $(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 3 \\ 3 \end{matrix}) + t \cdot (\begin{matrix} ‐ 3 \\ 2 \end{matrix})$ ;

$m$ met vergelijking $5 x + 2 y = 10$ .

Afspraak

Onder de hoek van twee snijdende lijnen verstaan we de grootte van de twee niet-stompe hoeken in het snijpunt.

Geef in graden nauwkeurig de hoek tussen de lijnen $k$ en $m$ van opgave 29.

(hint)

Je kunt bijgaande figuur maken.

Hoe groot is de hoek tussen een lijn met helling $\frac{2}{3}$ en een lijn met helling $‐ 1 \frac{1}{2}$ . Bepaal die hoek zonder je rekenmachine. Licht je antwoord toe.

Het inproduct is ook een handig instrument om de hoek tussen twee lijnen te bepalen. Hoe dat gaat zie je hieronder.

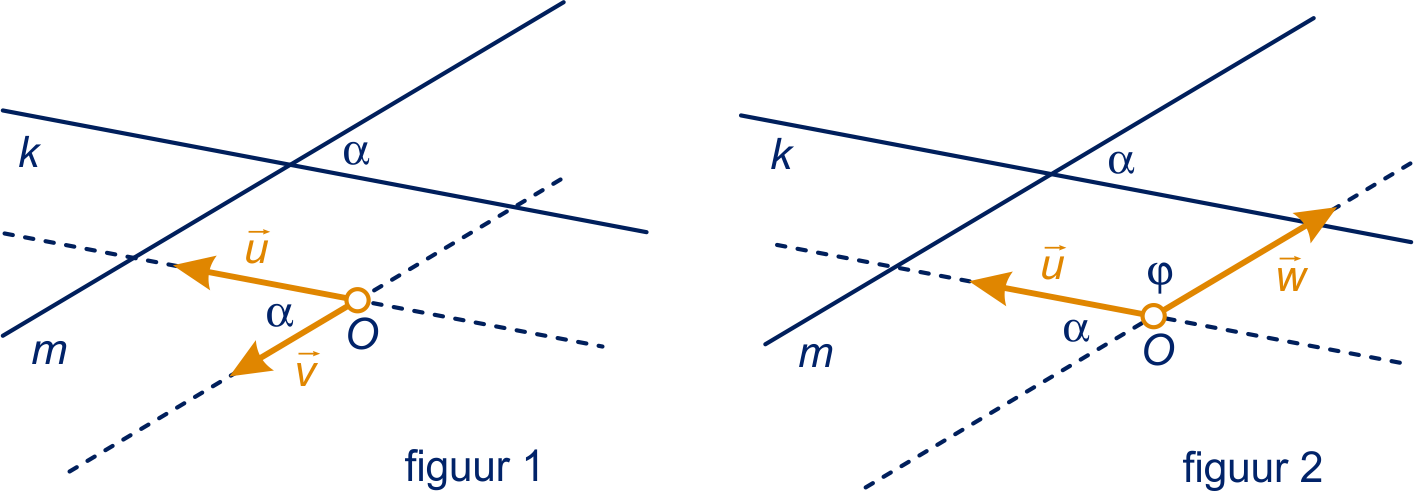
De (scherpe) hoek tussen de lijnen $k$ en $m$ is α. In figuur 1 is α ook de hoek tussen de gekozen richtingsvectoren $\vec{u}$ en $\vec{v}$ , dus
$\cos (α) = \frac{\vec{u} \cdot \vec{v}}{| \vec{u} | \cdot | \vec{v} |}$ .
In figuur 2 is de richtingsvector $\vec{w}$ gekozen (waarbij $\vec{w} = ‐ \vec{v}$ ).
De hoek $ϕ$ tussen de richtingsvectoren $\vec{u}$ en $\vec{w}$ is gelijk aan $180 ° - α$ , dus hier is
$\cos (α) = \cos (180 ° - ϕ) = ‐ \cos (ϕ) = ‐ \frac{\vec{u} \cdot \vec{w}}{| \vec{u} | \cdot | \vec{w} |}$ .
In beide gevallen geldt het volgende.

Als $\vec{v}$ en $\vec{w}$ richtingsvectoren van de lijnen $k$ en $m$ zijn en α de hoek tussen $k$ en $m$ , dan:
$\cos (α) = \frac{| \vec{v} \cdot \vec{w} |}{| \vec{v} | \cdot | \vec{w} |}$ .

In woorden kun je het zo formuleren.
De cosinus van de hoek α tussen twee lijnen $k$ en $m$ bereken je als volgt.
Kies richtingsvectoren $\vec{v}$ en $\vec{w}$ van de lijnen. Neem de absolute waarde van hun inproduct $| \vec{v} \cdot \vec{w} |$ en deel dat door het product van hun lengtes $| \vec{v} | \cdot | \vec{w} |$ .

Voorbeeld:

Gegeven zijn de lijnen $k$ met pv $(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 3 \\ 3 \end{matrix}) + t \cdot (\begin{matrix} ‐ 3 \\ 2 \end{matrix})$ en $m$ met vergelijking $5 x + 2 y = 10$ . Als richtingsvector van $k$ nemen we $\vec{v} = (\begin{matrix} ‐ 3 \\ 2 \end{matrix})$ . Een normaalvector van $m$ is $(\begin{matrix} 5 \\ 2 \end{matrix})$ , dus een richtingsvector is $\vec{w} = (\begin{matrix} 2 \\ ‐ 5 \end{matrix})$ . Het inproduct $\vec{v} \cdot \vec{w} = ‐ 16$ , de absolute waarde is dus $16$ . Het product $| \vec{v} | \cdot | \vec{w} |$ van hun lengtes is: $\sqrt{13} \cdot \sqrt{29}$ , dus voor de hoek α tussen $k$ en $m$ geldt: $\cos (α) = \frac{16}{\sqrt{13} \cdot \sqrt{29}}$ , dus α $\approx 34,5 °$ .
(Vergelijk dit resultaat met dat van opgave 30a.)

Bereken met behulp van het inproduct de hoek tussen de volgende vectoren in graden nauwkeurig.

$(\begin{array}{l} 1 \\ 1 \end{array})$ en $(\begin{matrix} 5 \\ 2 \end{matrix})$ ; $(\begin{matrix} ‐ 1 \\ 2 \end{matrix})$ en $(\begin{matrix} 5 \\ 1 \end{matrix})$ ; $(\begin{matrix} ‐ 1 \\ 1 \end{matrix})$ en $(\begin{array}{l} 7 \\ 1 \end{array})$ .

Bereken met het inproduct in graden nauwkeurig de hoek tussen de lijnen met pv
$(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 2 \\ 3 \end{matrix}) + t \cdot (\begin{matrix} 1 \\ 1 \end{matrix})$ en $(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 2 \\ 0 \end{matrix}) + t \cdot (\begin{matrix} 4 \\ 1 \end{matrix})$ .
En ook tussen de lijnen met pv
$(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 2 \\ 3 \end{matrix}) + t \cdot (\begin{matrix} ‐ 1 \\ 1 \end{matrix})$ en $(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 2 \\ 0 \end{matrix}) + t \cdot (\begin{matrix} 4 \\ 1 \end{matrix})$ .

Bereken de hoek tussen de $x$ -as en de lijn met pv
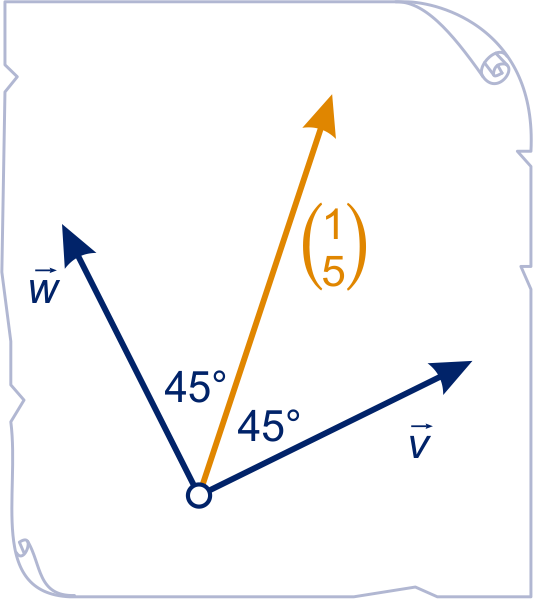
$(\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 2 \\ 3 \end{array}) + t \cdot (\begin{array}{l} 4 \\ 1 \end{array})$ .

Teken op roosterpapier de vector $(\begin{array}{l} 1 \\ 5 \end{array})$ en met hetzelfde beginpunt twee vectoren $\vec{v}$ en $\vec{w}$ die een hoek van $45 °$ met $(\begin{array}{l} 1 \\ 5 \end{array})$ maken; zie figuur.
De lengte van die vectoren ligt niet vast; maak het eerste kental van $\vec{v}$ gelijk aan $1$ en maak $\vec{w}$ even lang als $\vec{v}$ .
Wat denk je dat het tweede kental van $\vec{v}$ is?

Ga met een berekening na dat $(\begin{array}{l} 1 \\ 5 \end{array})$ en $(\begin{array}{l} 3 \\ 2 \end{array})$ een hoek van precies $45 °$ met elkaar maken.

Welke vector is $\vec{w}$ ?

Geef alle vectoren die een hoek van $45 °$ met de vector $(\begin{array}{l} 1 \\ 5 \end{array})$ maken.

$k$ en $m$ zijn twee snijdende lijnen. Lijn $p$ is een normaal van $k$ en lijn $q$ een normaal van $m$ .

Toon aan dat de hoek tussen $k$ en $m$ gelijk is aan de hoek tussen $p$ en $q$ .

De hoek tussen twee lijnen kun je dus ook bepalen door de hoek tussen hun normalen te berekenen.

De hoek van twee lijnen is gelijk aan de hoek tussen normalen van die twee lijnen.

Voorbeeld:

Gegeven zijn de lijnen $k$ met vergelijking $2 x + y = 10$ en $m$ met vergelijking $3 x + 4 y = 12$ .
Normalen van die lijnen hebben richtingsvectoren $(\begin{array}{l} 2 \\ 1 \end{array})$ en $(\begin{array}{l} 3 \\ 4 \end{array})$ . De hoek tussen de lijnen $k$ en $m$ noemen we $ϕ$ , dan $\cos (ϕ) = \frac{(\begin{array}{l} 2 \\ 1 \end{array}) \cdot (\begin{array}{l} 3 \\ 4 \end{array})}{| (\begin{array}{l} 2 \\ 1 \end{array}) | \cdot | (\begin{array}{l} 3 \\ 4 \end{array}) |} = \frac{2}{5} \sqrt{5}$ , dus $ϕ \approx 26,6 °$ .

Bereken de hoek tussen de lijnen $k$ en $m$ in graden nauwkeurig in de volgende gevallen.

$•$ $k : 2 x + 3 y = 5$	en	$m : 3 x - 4 y = 10$
$•$ $k : y = 2 x + 3$	en	$m : y = ‐ x + 3$

Als twee lijnen met helling $m$ en $n$ (beide niet $0$ ) loodrecht op elkaar staan, dan $m \cdot n = ‐ 1$ .

Laat dat zien met behulp van richtingsvectoren en het inproduct.

Geef een vergelijking in de vorm $y = m x + q$ van de lijn door $(4, ‐ 3)$ die loodrecht op de lijn $y = ‐ 1 \frac{1}{4} x + 7$ staat.

Voor welke $a$ staan de lijnen $2 x + 3 y - 12 = 0$ en $3 x - a y + 7 = 0$ loodrecht op elkaar?

De hellingshoek verdubbelen

$k$ is de lijn door $O$ en het punt $(4,2)$ .

Teken $k$ in een rooster.

Bereken de hellingshoek van $k$ in drie decimalen.

$p$ is de lijn door $O$ met een twee keer zo grote hellingshoek als $k$ .

Teken $p$ in hetzelfde rooster als $k$ .

Het lijkt erop dat $p$ door $(3,4)$ gaat.

Bereken de hellingshoek van de lijn door $O$ en $(3,4)$ in drie decimalen.

Uit b en d kun je alleen maar concluderen dat $p$ ongeveer door $(3,4)$ gaat. Je kunt dat zeker weten door de cosinus van de hoek tussen de vectoren $(\begin{array}{l} 1 \\ 0 \end{array})$ en $(\begin{array}{l} 4 \\ 2 \end{array})$ en die tussen de vectoren $(\begin{array}{l} 4 \\ 2 \end{array})$ en $(\begin{array}{l} 3 \\ 4 \end{array})$ te berekenen.

Doe dat.

Tel de vectoren $(\begin{array}{l} 5 \\ 0 \end{array})$ en $(\begin{array}{l} 3 \\ 4 \end{array})$ op. Leg uit hoe hieruit volgt dat $p$ door $(3,4)$ gaat.

In opgave 37 zullen we het volgende bewijzen.
De lijn met helling $\frac{2 m}{1 - m^{2}}$ heeft een twee keer zo grote hellingshoek als de lijn met helling $m$ , $m \neq ‐ 1$ en $m \neq 1$ .

Waarom moet hierboven $m \neq ‐ 1$ en $m \neq 1$ zijn?

Ga na dat volgens het bovenstaande de lijn met richtingsvector $(\begin{array}{l} 3 \\ 4 \end{array})$ een twee keer zo grote hellingshoek heeft als de lijn met richtingsvector $(\begin{array}{l} 4 \\ 2 \end{array})$ .

Een lijn met hellingshoek $30 °$ heeft helling $\frac{1}{3} \sqrt{3}$ en een lijn met hellingshoek $60 °$ heeft helling $\sqrt{3}$ .

Laat zien dat dit in overeenstemming is met bovenstaande formule.

De lijn met helling $\frac{2 m}{1 - m^{2}}$ heeft een twee keer zo grote hellingshoek als de lijn met helling $m$ , $m \neq ‐ 1$ en $m \neq 1$ .

In de volgende twee opgaven geven we twee bewijzen van bovenstaande, het eerste met gelijkvormigheid, het tweede met het inproduct.

Zie de figuur voor de gegevens. Bovendien is $O S = 1$ . De lijn $O Q$ heeft dus helling $m$ . De hellingshoek van lijn $O P$ is $2$ keer zo groot als die van $O Q$ .

Laat zien dat de driehoeken $O Q S$ en $Q R S$ gelijkvormig zijn.

Druk de lengte van $R S$ en de coördinaten van $R$ uit in $m$ .

$Q (1, m)$ is het midden van $P R$ .

Waarom?

Bepaal daarmee de coördinaten van $P$ en leid hieruit af dat lijn $O P$ helling $\frac{2 m}{1 - m^{2}}$ heeft.

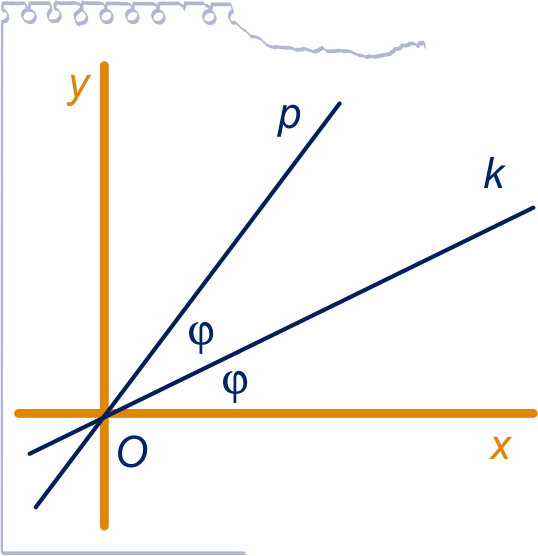
In plaats van het bewijs met gelijkvormigheid in opgave 37, kunnen we ook een bewijs met het inproduct geven.
In de figuur hiernaast heeft $k$ helling $m$ en hellingshoek ϕ; $p$ heeft hellingshoek $2$ ϕ. De helling van $p$ noemen we $x$ .

Laat zien dat dan $(\begin{array}{l} 1 \\ 0 \end{array}) \cdot (\begin{array}{l} 1 \\ m \end{array}) = \cos (ϕ) \cdot \sqrt{1 + m^{2}}$ en $(\begin{array}{l} 1 \\ x \end{array}) \cdot (\begin{array}{l} 1 \\ m \end{array}) = \cos (ϕ) \cdot \sqrt{1 + m^{2}} \cdot \sqrt{1 + x^{2}}$ .

Laat zien dat uit a volgt: $1 + m x = \sqrt{1 + x^{2}}$ .

Bereken nu $x$ met behulp van het vorige onderdeel, dat wil zeggen, druk $x$ uit in $m$ .

Zie de figuur hiernaast voor de gegevens.

Bereken $x$ exact.