;
;
-
, en
de helling is

De gevraagde hoek dus .
Richtingsvectoren van die lijnen zijn: en . Het inproduct van deze vectoren is , dus de hoek is .
, ,
In het eerste geval is het de hoek tussen en
, die is: .
In het tweede geval bereken je de hoek tussen de vectoren en
, die is
, dus de gevraagde hoek is
.
De hellingshoek van die lijn is , dus de hoek tussen de lijnen is .
Aflezen in het rooster: .
Dat zijn de positieve veelvouden van en van .
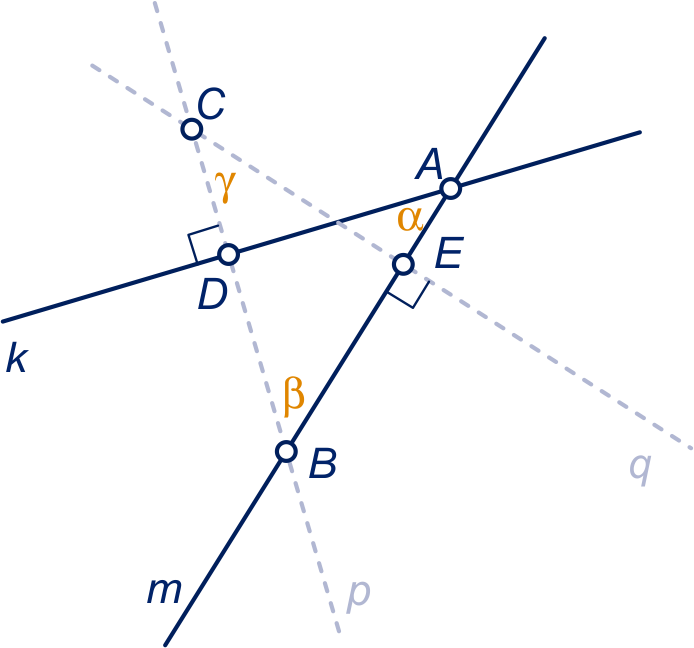
De hoekensom in driehoek geeft:
;
de hoekensom in driehoek geeft:
, dus
α = γ.
In het eerste geval:
.
In het tweede geval:
een richtingsvector van is
en van
is . Voor de hoek tussen de lijnen vind je: .
Richtingsvectoren zijn en
.
Als de lijnen loodrecht op elkaar staan is het inproduct van deze vectoren .
De helling is dan , dus een vergelijking is: .
, dus .
-
graden
-
graden
In beide gevallen vind je .
De vectoren en
zijn even lang; als je ze optelt volgens de parallellogrammethode krijg je een vector
die de hoek tussen en
middendoor deelt. (Eigenschap van een ruit: diagonaal deelt hoeken middendoor.)
.
Anders wordt de noemer van nul.
Als en
, maakt de lijn een hoek van met de -as en krijg je een verticale lijn bij verdubbelen van de hellingshoek.
De richtingscoëfficiënt bij richtingsvector is is en bij richtingsvector is die .
invullen in
geeft .
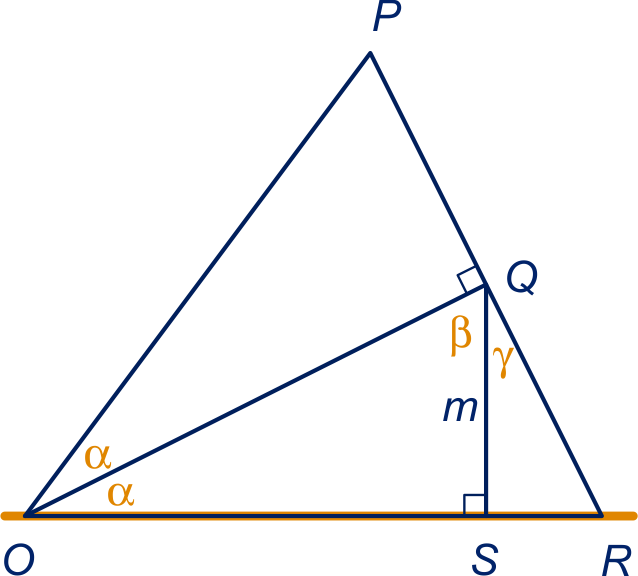
(hoekensom in driehoek ) en (rechte hoek), dus .
Uit a volgt dat , dus , dus , dus .
Omdat de driehoeken en congruent zijn, want de hoeken bij zijn beide recht, de hoeken bij zijn gelijk en ze hebben zijde gemeenschappelijk.
, dus .
In beide gevallen is dit de inproductregel.
Uit het eerste deel van a volgt: en uit het tweede deel: . Als je voor in het tweede deel invult krijg je: .
Kwadrateren geeft: , dus .
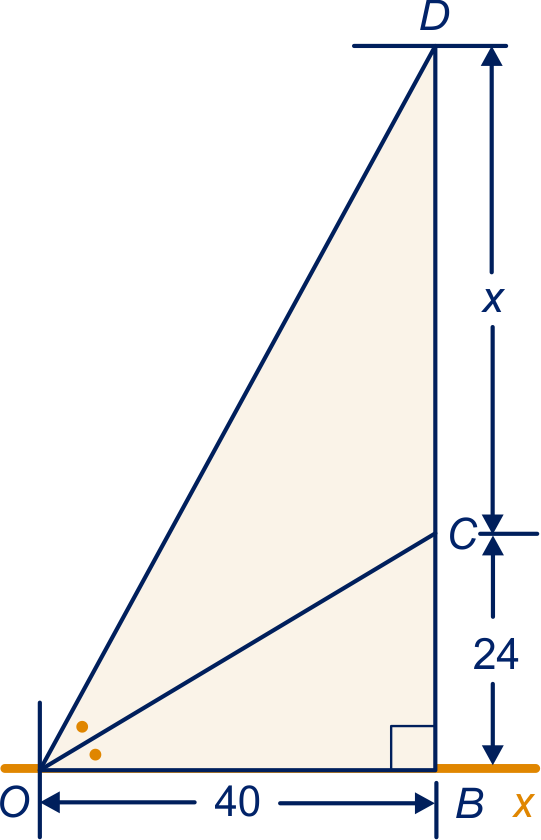
Helling , dus
helling , maar de helling van
is ook: , dus:
.
Kruislingsvermenigvuldigen levert dan: .
