De uiterste punten van de boog links en rechts noemen we en .
Het midden van noemen we
, de straal van de cirkel en het middelpunt .
Dan is driehoek rechthoekig in
; ,
en
.
De stelling van Pythagoras in driehoek geeft de vergelijking
, dus
, dus
cm.
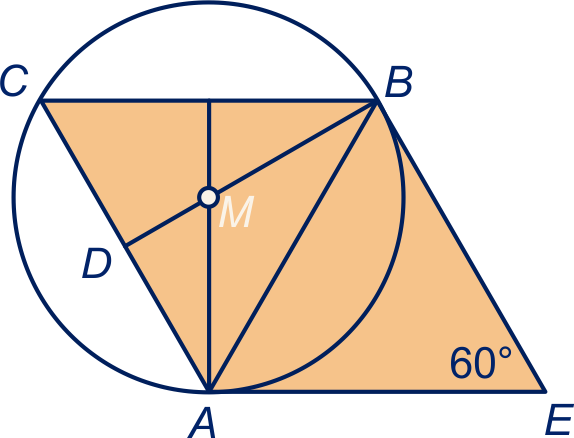
Diagonaal snijdt de ruit in twee regelmatige driehoeken. is het snijpunt van de symmetrieassen van driehoek . Dit punt is het middelpunt van de cirkel. De straal is , want driehoek is een -- graden driehoek met .
;
;
cirkelsector heeft oppervlakte
.
De gevraagde oppervlakte is dus .
Uit de stelling van Pythagoras volgt: , dus .
Het middelpunt van de cirkel is: . , dus .
Dan moet lijn de cirkel raken. Het raakpunt ligt op de lijn door loodrecht ; heeft vergelijking . De raakpunt is dus: . Dit punt moet op de cirkel liggen, dus: .
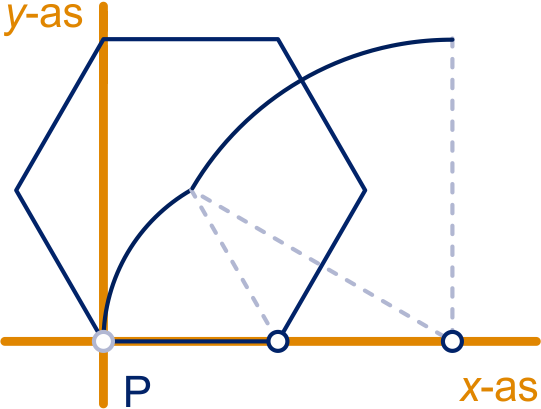
Het eerste stuk is een cirkelboog van , met middelpunt en straal . Het tweede stuk is een cirkelboog van met middelpunt en straal .
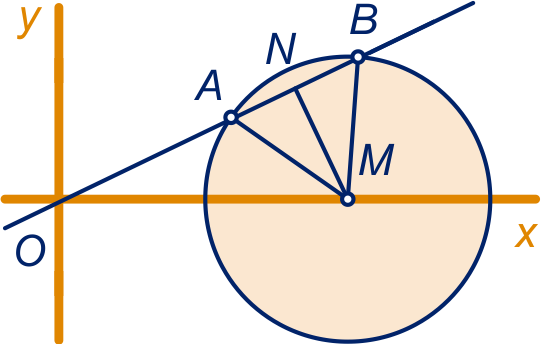
Zie figuur.
Er geldt: , omdat de helling van lijn
gelijk is aan .
Noem , dan
, dus
(stelling van Pythagoras): , dus
en
en .
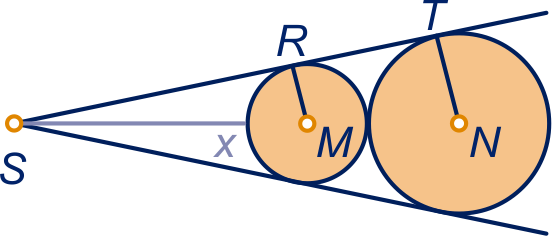
Zie figuur.
Er geldt: en . De driehoeken
en
zijn gelijkvormig, want ze hebben beide een rechte hoek en hoek
gemeenschappelijk, dus
, dus
.
De cirkel heeft vergelijking , het middelpunt is dus en de straal . De gezochte punten liggen dus op de cirkel middelpunt en straal . De punten zijn dus oplossing van het stelsel: , dus en .
is de ketting , dus
. De raaklijn in
aan de grafiek van heeft
helling , dus de raaklijn aan de cirkel ook.
ligt op de lijn door
loodrecht op de raaklijn. Lijn heeft
dus helling . Een vergelijking van lijn
is dus:
. Dus
.
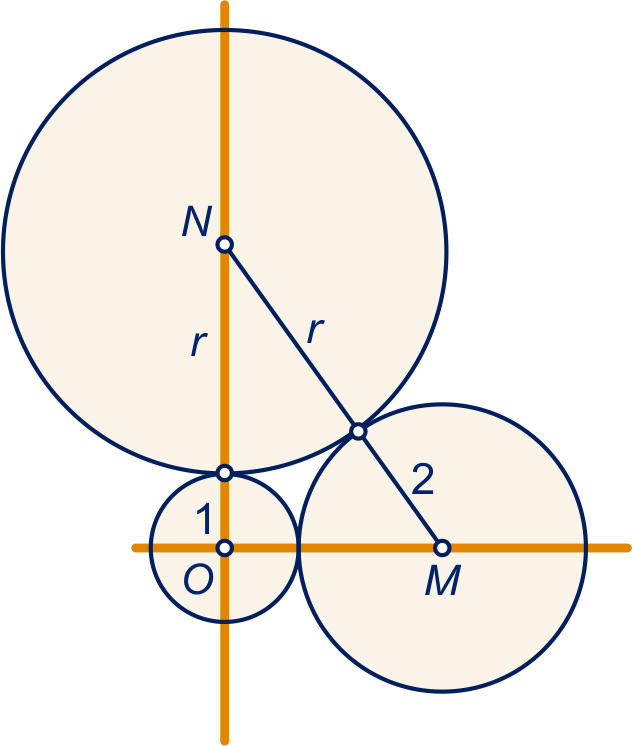
Noem de straal van de derde cirkel . Uit de stelling van Pythagoras volgt:
, dus
.
Het middelpunt van de cirkel is dan
en een vergelijking:
.
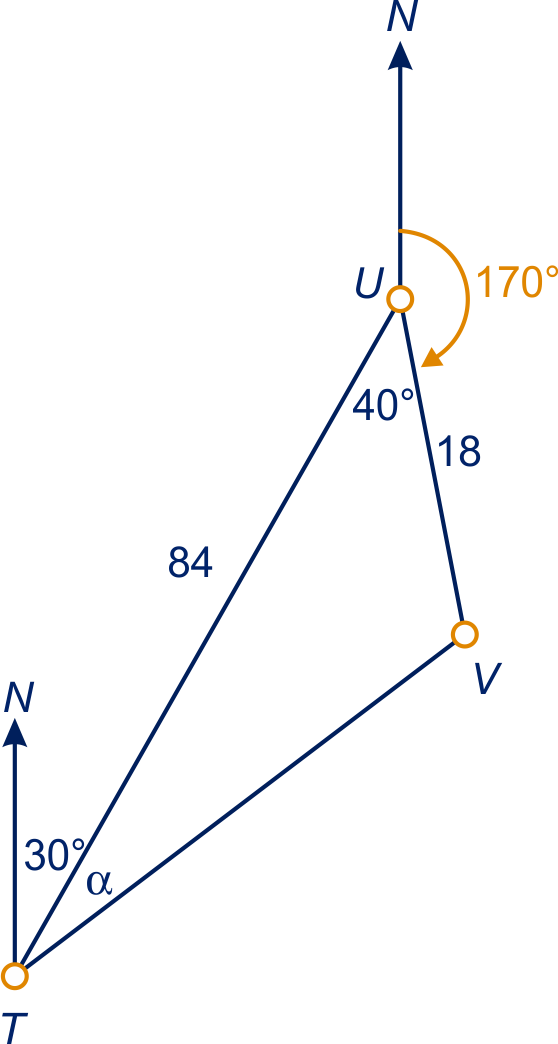
Uit de cosinusregel in driehoek volgt:
, dus
.
Uit de sinusregel in driehoek volgt:
, dus
en
de koershoek is .
Het middelpunt van de cirkel is en de straal , dus de afstand van tot is: . De afstand van tot de cirkel is dus: .
De lijn door loodrecht op heeft vergelijking . Het snijpunt met is . De afstand van tot is: , dus de afstand van tot de cirkel is de afstand van tot de cirkel is .
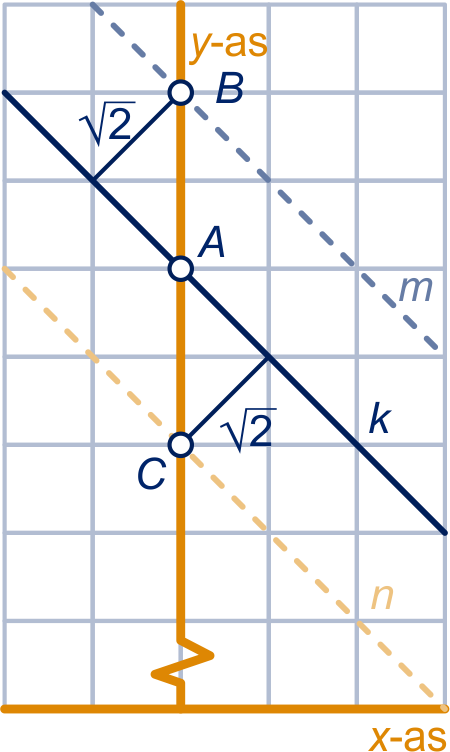
Die lijnen zijn evenwijdig met . Noem ze en . Ze hebben beide een vergelijking van de vorm: . We zoeken een punt op elk van die lijnen. Het punt ligt op . De punten en liggen dan op en . Dus de lijnen hebben vergelijking en .
De bodem is vierkant met zijden en de hoogte is , dus de inhoud is .
Als de inhoud maximaal is voor een bepaalde waarde van , dan
.
, dus
(dus klopt).
gaat door , dat geeft ; dus parabool .
invullen geeft
en (vanwege symmetrieas ) .
Oppervlakte rechthoek .
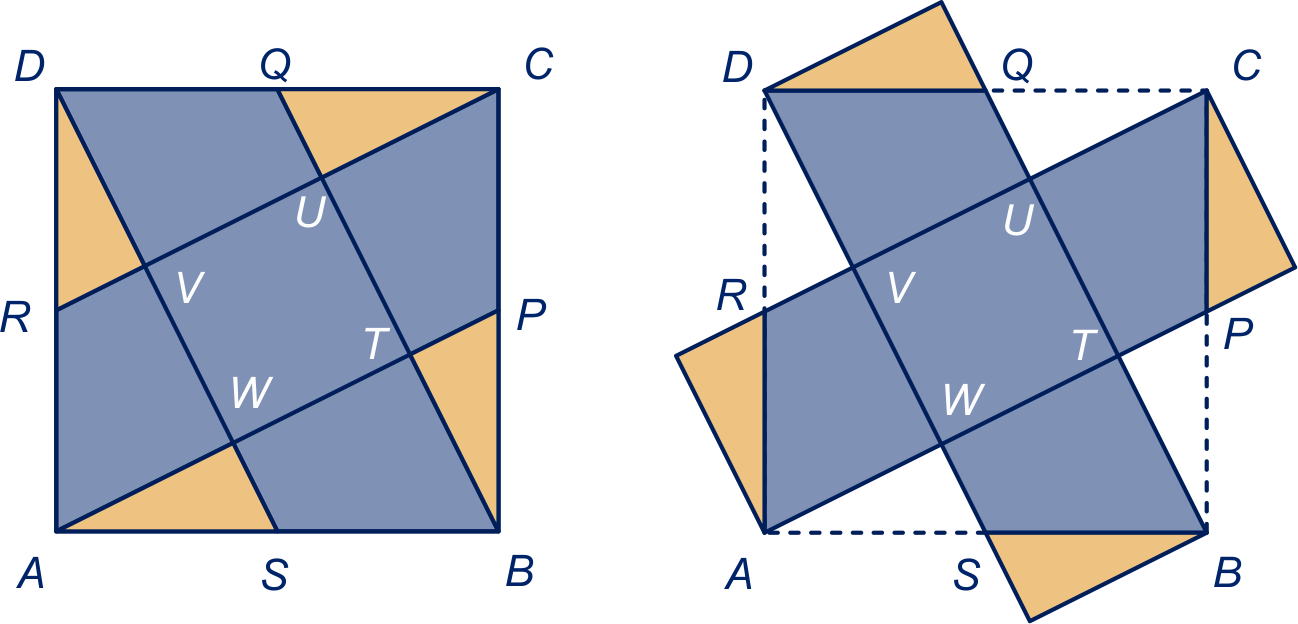
De driehoeken en
zijn gelijkvormig.
Beide hebben een rechte hoek en ze hebben hoek gemeenschappelijk.
en , dus de vergrotingsfactor is
. Dus
en
. Dan
en de
gevraagde oppervlakte is .
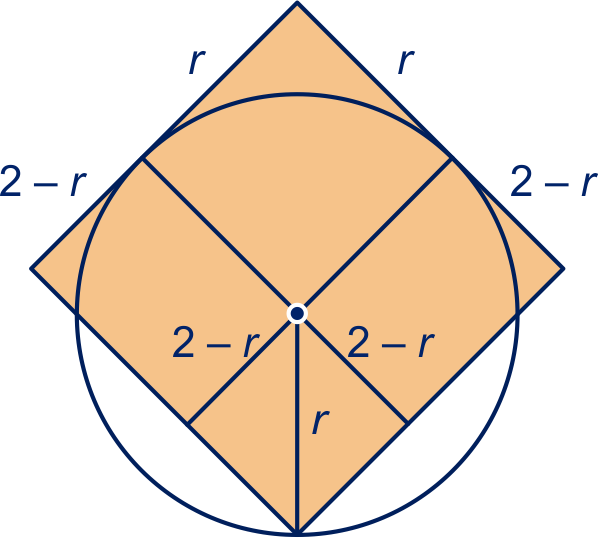
Een mooiere oplossing vind je met 'knippen en plakken'. In de figuur hierboven rechts zie je dat de gevraagde oppervlakte
van de
oppervlakte van vierkant is.
Noem die eerste coördinaat , dan . Er geldt: , dus , dus .
Noem die eerste coördinaat , dan is de eerste coördinaat van gelijk aan , dus , dus . Dus .
Dan , dus .
De oppervlakte van de rechthoek is . Met de GR zie je dat maximaal is als , dus .
Lijn moet door het punt gaan. Dus een vergelijking is: . Dus de eerste coördinaat van is oplossing van de vergelijking . Met bijvoorbeeld de abc-formule vind je of . Dus de eerste coördinaat van is .
Er geldt: voor alle , dus de -as is symmetrieas.
Omdat de -as symmetrieas is, snijden de raaklijnen elkaar in de
-as.
, dus de snijpunten
met de -as zijn en
.
Met de GR de helling bepalen bij geeft
(of met de kettingregel, geen examenstof:
, dus
).
Dus een vergelijking van de raaklijn in
is
.
Het gevraagde snijpunt is .
De verschoven functie noemen we . Neem aan dat de grafiek van over
eenheden verschoven wordt, dan
en
,
dus
, dus
.
