Het middelpunt noemen we en het punt
noemen we . Dan heeft lijn
richtingscoëfficiënt , dus de raaklijn heeft richtingscoëfficiënt .
Een vergelijking van de raaklijn is dus: .
Het middelpunt van de cirkel is .
Noem het raakpunt ,
dan staat lijn loodrecht op de lijn
, heeft dus richtingscoëfficiënt .
Dus lijn heeft vergelijking
.
We bepalen het snijpunt van lijn met de cirkel.
.
Dus het raakpunt is of
, dus
of .
Lijn
heeft richtingscoëfficiënt ,
dus lijn heeft richtingscoëfficiënt
,
dus een vergelijking van lijn
is: (want ligt erop.)
snijden met
geeft:
.
Van naar ga je naar rechts en naar beneden, dus van naar moet je dat nog eens doen. Je komt dan in .
Het midden van de rechthoek is het
middelpunt van de cirkel door de hoekpunten van de rechthoek, dus ook het middelpunt van de cirkel door de punten ,
en . Het middelpunt is dus het midden van
dus .
De straal is .
Lijn heeft richtingscoëfficiënt , dus lijn heeft richtingscoëfficiënt . Een vergelijking van lijn is dus: . snijden met geeft .
De hoeken en zijn even groot en beide driehoeken hebben een rechte hoek. De vergrotingsfactor is .
De straal is .
,
dus middelpunt
en straal ;
,
dus middelpunt
en straal ;
;
middelpunt
en straal .
Het middelpunt van
die cirkel ligt op de lijn door loodrecht op de lijn ,
dus op de lijn .
ligt ook op afstand van ,
dus op de cirkel met vergelijking .
Het gezochte middelpunt is oplossing van het volgende stelsel.
.
Dus
of .
Het middelpunt ligt op de lijn door loodrecht op de lijn .
Het middelpunt ligt dus op de lijn .
Het middelpunt ligt ook op de middelloodlijn van
en , dus op de lijn ,
dus het middelpunt is .
Het raakpunt ligt op de lijn door
loodrecht op de lijn met vergelijking ,
dus op de lijn met vergelijking .
Het raakpunt is dus oplossing van het stelsel:
, dus het raakpunt is:
of ,
dus of
.
.
Lijn heeft richtingscoëfficiënt , dus
heeft richtingscoëfficiënt ,
dus
heeft vergelijking . Het punt
voldoet aan de vergelijking, dus een vergelijking van
is:
.
voldoet aan deze vergelijking, dus het klopt.
,
dus lijn heeft richtingscoëfficiënt .
Lijn heeft richtingscoëfficiënt ,
dus en lijn
staan loodrecht op elkaar, dus is de raaklijn aan
in .
en .
Het midden van lijnstuk noemen we
, dan is .
Lijn staat loodrecht op lijn
, want driehoek
is gelijkbenig, dus de afstand is
.
Het raakpunt ligt op de lijn , is dus
of
.
Een vergelijking van de raaklijn is dus: of
.
Lijn : ; lijn :
Snijpunt:
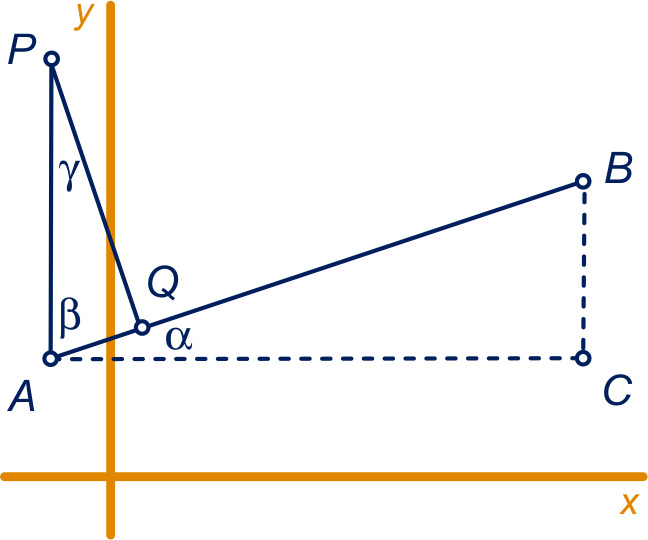
en , dus . Verder hebben beide driehoeken een rechte hoek.
,
dus
.
Als je als basis neemt, is de bijbehorende hoogte , de oppervlakte is dus: .
Oppervlakte driehoek
,
dus .
Dat is het snijpunt van de cirkel met lijn .
Een vergelijking van de cirkel is: en een vergelijking van
lijn is
Voor invullen in de vergelijking van de cirkel geeft:
, dus
.
De snijpunten zijn dus en
.
Het punt ligt het dichtst bij
.
en , dus .
Beide hebben een rechte hoek, verder hebben ze hoek hetzelfde.
De factor is: , dus: en , dus .
Het midden van lijnstuk noemen we
, dan is driehoek een
---graden driehoek.
Dus die afstand is .
De hellingshoek van lijn is
, dus de richtingscoëfficiënt is
.
Een vergelijking van lijn is dus:
.
.
De loodrechte projectie van op de -as noemen we . Dan is een ---graden driehoek, dus en , dus .
