Het midden van het lijnstuk met eindpunten en is .
Twee lijnen en
zijn niet evenwijdig aan de assen.
Dan:
en
staan loodrecht op elkaar
het product van hun richtingscoëfficiënten is gelijk aan .
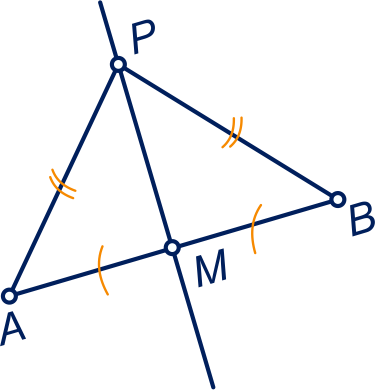
Gegeven twee punten en .
De punten die even ver van als van
liggen, vormen de middelloodlijn van AB.
Deze lijn gaat door het midden van lijnstuk en staat loodrecht op lijn .

De omgeschreven cirkel van een driehoek is de cirkel die door de hoekpunten van de driehoek gaat.
Het middelpunt van deze cirkel is het snijpunt van de middelloodlijnen van de zijden.
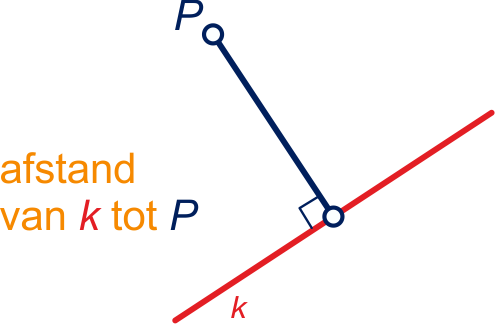
De afstand van tot
is
.
De afstand van een punt tot een gebied is de lengte van het kortste verbindingslijnstuk van dat punt met het gebied.
De cirkel met middelpunt en straal heeft vergelijking: .
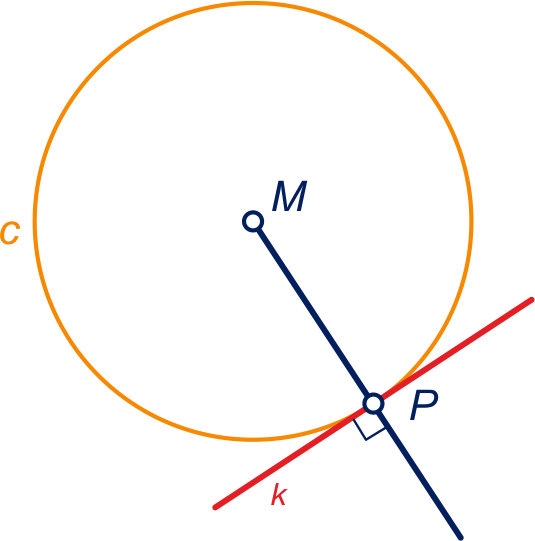
We zeggen: een cirkel raakt een lijn
als en
precies één punt, het raakpunt, gemeen hebben.
Als middelpunt
heeft en het raakpunt is, dan staat lijn
loodrecht op .