Teken op de GR de grafiek van de functie .
Bereken algebraïsch de richtingscoëfficiënt van de raaklijn aan de grafiek in het punt met en ook in het punt met .
Stel langs algebraïsche weg een vergelijking op van de raaklijn aan de grafiek van in elk van deze punten.
Bereken algebraïsch de coördinaten van de punten van de grafiek waarin de raaklijn horizontaal is.
Hoe zie je aan de formule van dat de grafiek symmetrisch is in het punt ?
en .
Bereken algebraïsch voor welke geldt: .
Bereken algebraïsch voor welke geldt: .
Bereken algebraïsch voor welke geldt: .
Bereken algebraïsch voor welke geldt: .
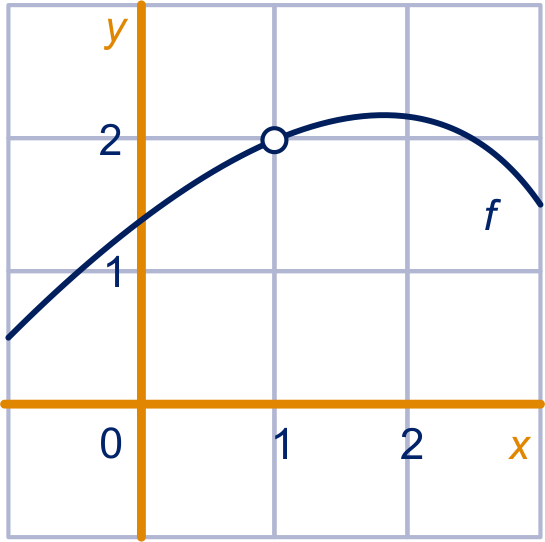
Hiernaast staat de grafiek van een functie , waarvan de formule onbekend is.
Anneke kent de formule wel en heeft daarmee de gemiddelde helling uitgerekend op het interval
.
Ook heeft Anneke de gemiddelde helling uitgerekend op het interval
.
Tenslotte heeft Anneke de gemiddelde helling uitgerekend op het interval
.
Welke van de drie gemiddelde hellingen is het kleinst en welke het grootst? Waarom?
Welke van de drie gemiddelde hellingen is de beste benadering van de helling van de grafiek van in het punt zelf? Waarom?
Van een functie weten we een formule voor de afgeleide functie:
. Bovendien weten we dat de grafiek door het punt
gaat.
Stel een formule op van de functie .
Laat zien dat .
Geef en zo groot mogelijk -interval waarop de functie dalend is.
De snelste hardloper in de dierenwereld is de cheetah. Hij kan erg snel een grote snelheid bereiken; hij kan echter deze grote snelheid maar kort volhouden.

We rekenen de tijd in seconden. Op tijdstip staat de cheetah nog stil. Dan begint hij met zijn sprint.
Na seconden is die afgelopen.
De afgelegde weg noemen we (in meters).
Er gelden de volgende formules:
|
|
voor , |
|
|
voor , |
|
|
voor . |
Hoe groot is de afstand die de cheetah aflegt?
Bereken de gemiddelde snelheid gedurende de eerste seconden.
Bereken de gemiddelde snelheid gedurende de totale seconden.
Bereken op welke tijdstippen de snelheid van de cheetah m/s was.
Wat is de versnelling in elk van de drie periodes van seconden? (De versnelling is de afgelede van de snelheid.)
Schets (zonder te rekenen) de vorm van de tijd-afstand-grafiek voor .
Teken op de GR de grafiek van .
Bereken algebraïsch de nulpunten van .
Bereken de hoek die de grafiek van met de -as maakt in de oorsprong.
Bereken exact de -coördinaten van de punten van de grafiek van waar de richtingtingscoëfficiënt is.
Stel langs algebraïsche weg een vergelijking op van de raaklijn aan de grafiek in het punt met eerste coördinaat .
Stel langs algebraïsche weg een vergelijking op van de buigraaklijn. Laat de breuken in je antwoord staan.
Teken op de GR de grafiek van .
Bereken exact de coördinaten van de punten op de grafiek waar de helling is.
Er zijn twee raaklijnen aan de grafiek met helling . Eén van die raaklijnen heeft vergelijking .
Bereken langs algebraïsche weg een vergelijking van de andere raaklijn met helling .
Controleer je antwoord met de GR.
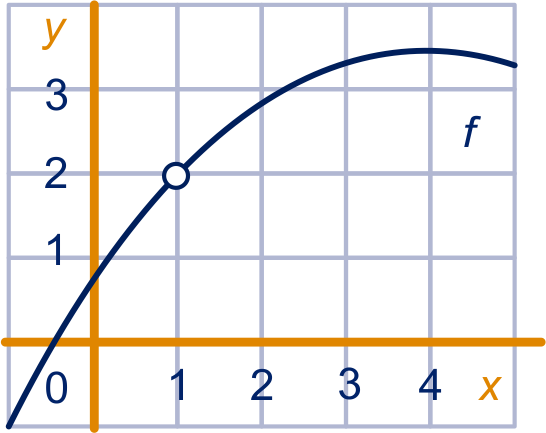
Hiernaast staat de grafiek van een functie met daarop het punt . De punten en liggen ook op de grafiek, dicht bij : en .
Hoe groot schat jij op grond hiervan dat de helling van de grafiek in het punt is?
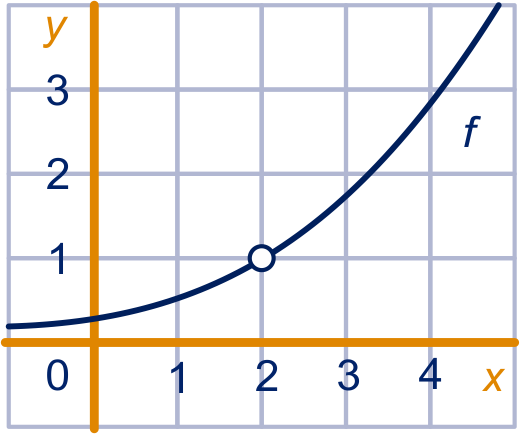
Hiernaast staat de grafiek van een functie . Gegeven is dat en .
Stel een vergelijking op van de raaklijn aan de grafiek van in het punt met .
De functie is drie maal de functie
plus .
Dus: .
Stel een vergelijking op van de raaklijn aan de grafiek van in het punt met .
Teken op de GR de grafiek van .
Los algebraïsch op: .
Bereken op welk interval dalend is.
Stel algebraïsch een vergelijking op van de raaklijn aan de grafiek van in het punt met .
Een horizontale lijn snijdt de grafiek van in drie verschillende punten.
Bereken voor welke getallen dat het geval is.

Een ballon wordt losgelaten op tijdstip . Hieronder staat de tijd-hoogte-grafiek van de ballon. De hoogte boven de grond wordt gemeten in meters, de tijd in seconden.

Wanneer stijgt de ballon het snelst, in het begin of later?
Bepaal met behulp van de grafiek de gemiddelde stijgsnelheid (in m/s) van de ballon op het tijdsinterval .
Bepaal met behulp van de grafiek de stijgsnelheid (in m/s) van de ballon op het tijdstip .
Schets de grafiek van de stijgsnelheid als functie van de tijd.
.
Schrijf de formule van deze parabool met behulp van kwadraatafsplitsen in de topvorm.
Hoe volgt uit het antwoord van vraag a wat de minimale waarde van is?
Controleer je antwoord op vraag b met differentiëren.
Hieronder is van een functie aangegeven waar positief, nul en negatief is en ook waar positief, nul en negatief is.
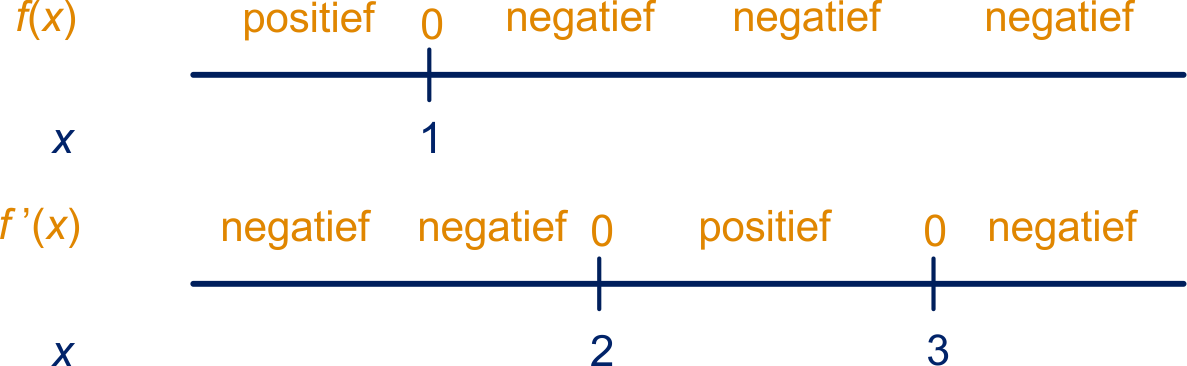
Schets de grafiek van een mogelijke functie .
Hieronder staat de tijd-afstand-grafiek van een auto.
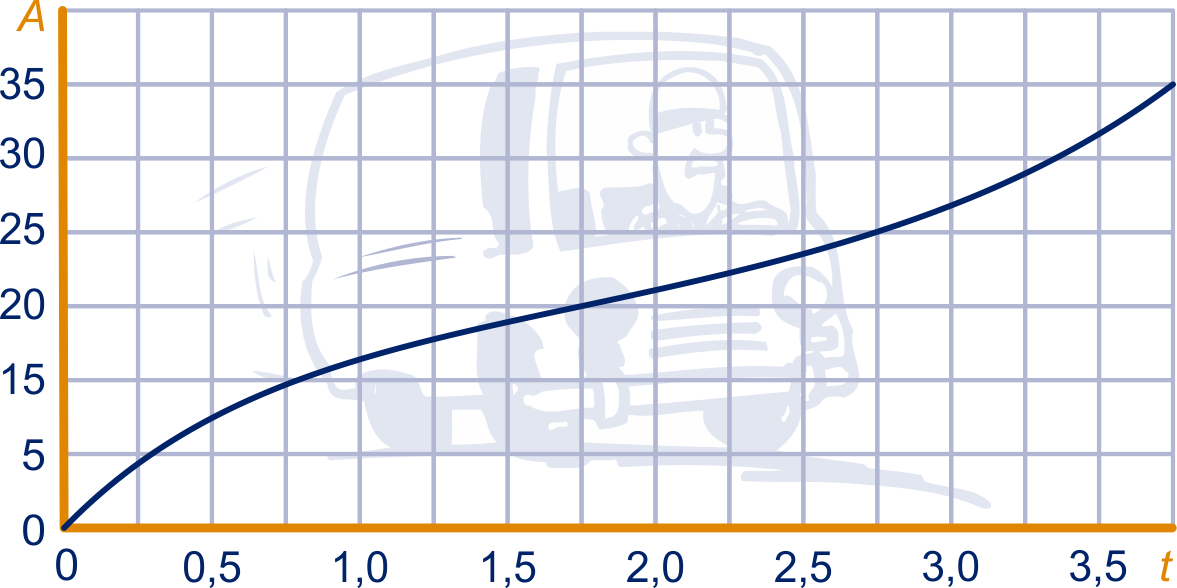
Je kunt goed zien dat de weg waarover de auto reed een vrij scherpe bocht maakte.
Waaraan zie je dat?
Een bijbehorende formule is: , waarbij de afstand is in hectometers (gerekend vanaf een zeker punt langs de weg) en de tijd is in minuten.
Geef een formule voor de snelheid van de auto (in hectometers per minuut).
Bereken algebraïsch op welke tijdstippen de snelheid
km/uur is. Rond je antwoorden af op 2 decimalen.
Let op de eenheid!
Teken op de GR de grafiek van de functie .
Bereken exact de coördinaten van de snijpunten van de grafiek van met de -as.
Bereken exact het minimum van .
Verder is gegeven de functie .
Bepaal zodat de grafiek van de -as raakt.
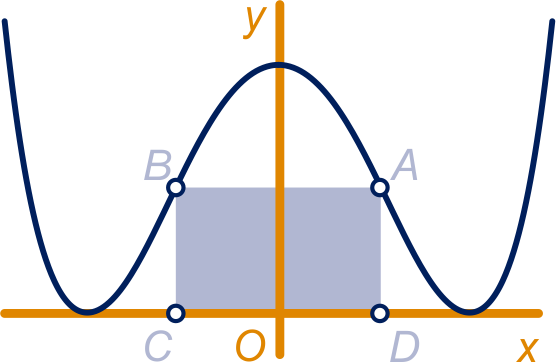
Op de grafiek van liggen punten en op gelijke hoogte. De -coördinaat van noemen we . We maken een rechthoek met punten en op de -as zoals in de figuur.
Leg uit dat de oppervlakte van rechthoek gelijk is aan .
Bereken met differentiëren voor welke waarde van de oppervlakte van rechthoek maximaal is. Rond je antwoord af op 3 decimalen.
Hieronder is een deel van de parabool
getekend en een deel van de lijn .
De punten
en
liggen op de parabool.
Het lijnstuk
snijdt de lijn
in het punt .
is het snijpunt van de parabool en de lijn
.
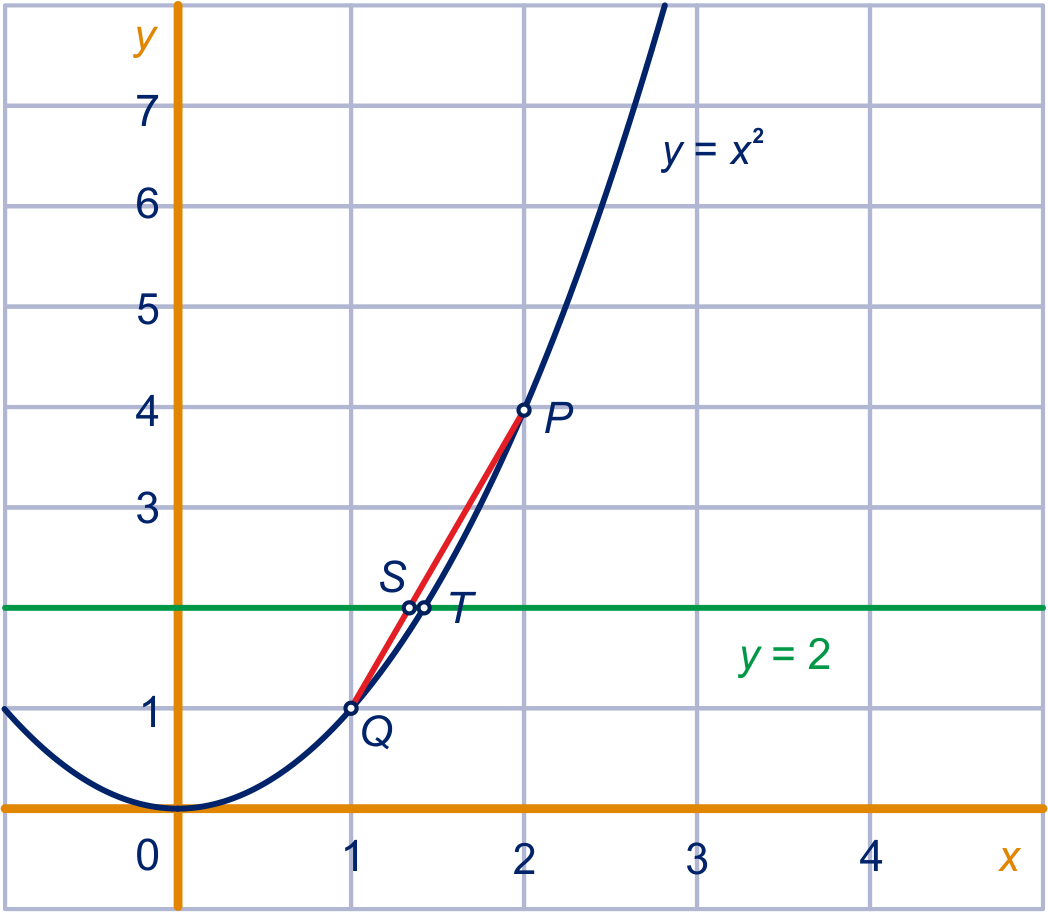
Bereken de lengte van in twee decimalen.
Bij de volgende vragen laten we tussen en over de parabool bewegen, terwijl het punt blijft. Lijnstuk verandert steeds van richting en punt verandert van plaats. De -coördinaat van noemen we .
Toon aan dat de richtingscoëfficiënt van gelijk is aan .
Toon aan dat de -coördinaat van is:
.
Bereken voor welke waarden van de lengte van lijnstuk kleiner is dan . Geef de grenzen in twee decimalen nauwkeurig.
Een piramidevormige trechter is aan de bovenkant open. De bovenkant is bij cm en de diepte van de trechter is dm. We gieten water in de trechter.
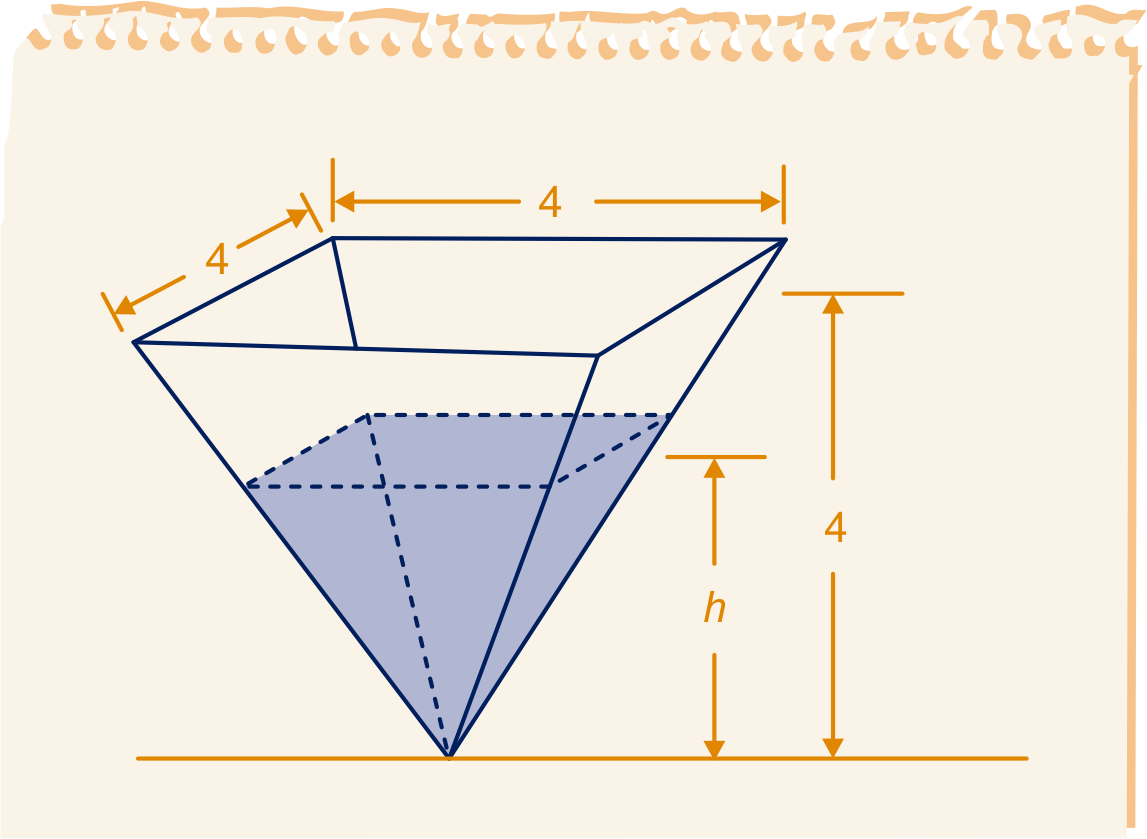
De waterhoogte noemen we , de bijbehorende oppervlakte van de waterspiegel noemen we en de waterinhoud .
Druk uit in .
Gegeven is dat .
Welke formule voor volgt hieruit?
Hoeveel dm³ water kan de trechter bevatten?
