Uitgaande van de machtsfuncties kun je door middel van optellen, aftrekken, vermenigvuldigen en delen nieuwe functies bouwen. Bijvoorbeeld . In het vervolg gaan we leren dergelijke functies te differentiëren; dat wil zeggen: we gaan de afgeleide daarvan berekenen.
Omdat in de volgende paragrafen nogal vaak meerdere functies tegelijk gebruikt worden, moeten we de functies een naam geven om ze van elkaar te kunnen onderscheiden.
Voor functies worden vaak de namen ,
en gebruikt.
Bijvoorbeeld: is de functie
en is de functie
.
Dan schrijven we meestal
en .
Deze laatste manier van opschrijven noemen we de
functienotatie.
Voor de afgeleide van een functie geldt eenzelfde notatie:
en .
Van de functie
kennen we de afgeleide: .
Kennen we dan automatisch ook de afgeleide van de functies
en
?
Daarover gaat deze paragraaf.

Een goederentrein van meter lengte is aan het rangeren. Hieronder staat in het linker plaatje de tijd-afstand-grafiek van de voorkant van de locomotief. De afstand is gemeten vanaf een zekere seinpaal op het station. De locomotief staat met zijn voorkant naar die seinpaal toe.
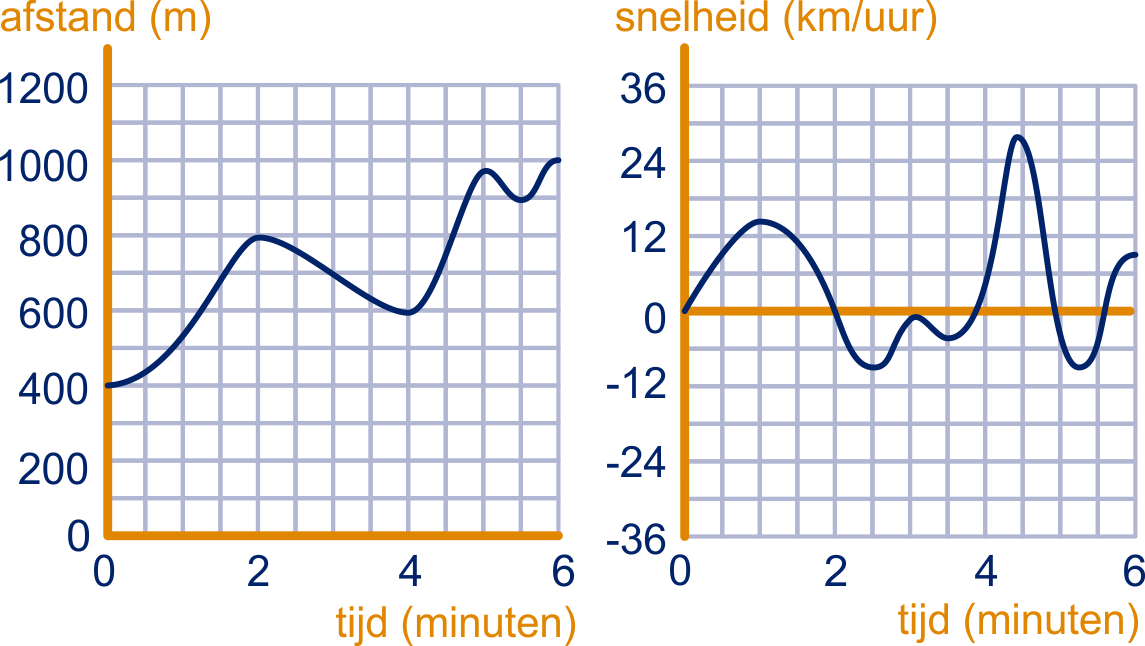
Hoe kun je de tijd-afstand-grafiek van de achterkant van de laatste wagon tekenen?
In het rechter plaatje zie je de tijd-snelheid-grafiek van de locomotief. De snelheid bij het achteruitrijden is negatief getekend.
Wat weet je van de tijd-snelheid-grafiek van de laatste wagon?
Conclusie
Als je de grafiek van een functie verticaal verschuift, verandert de helling van de grafiek niet.
Als je bij een functie een constant getal optelt, houd je dezelfde afgeleide functie.
In functienotatie:
Als , voor een constante
, dan
.
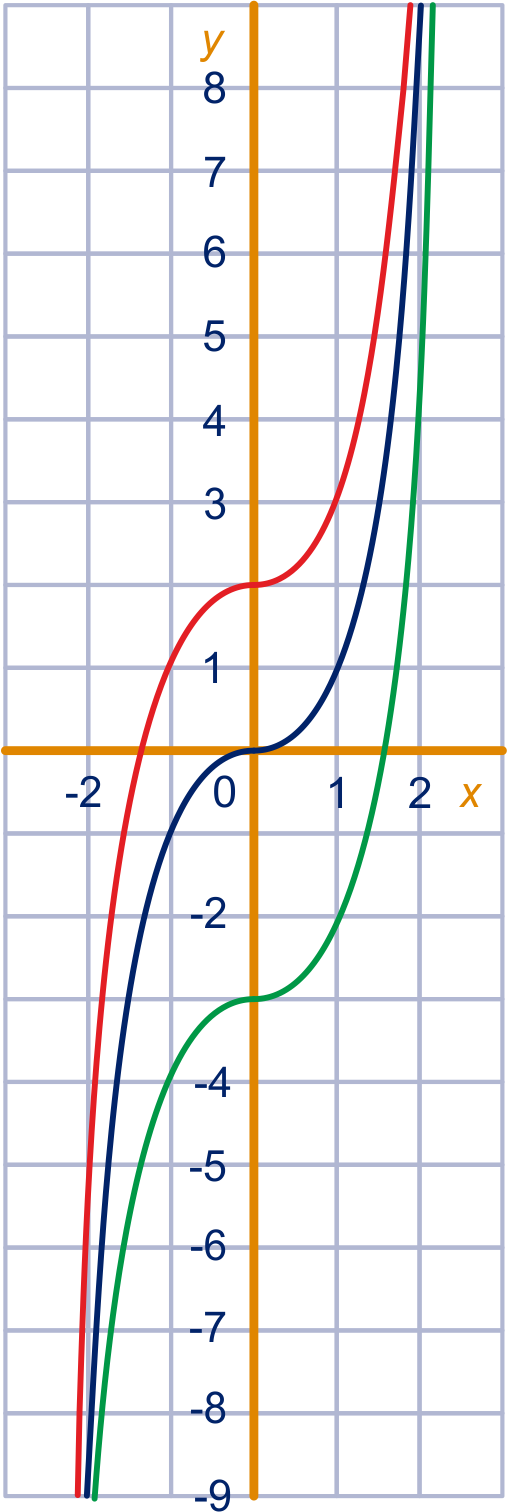
Hiernaast staan de grafieken van drie functies:
,
en .
Controleer de grafieken voor en .
Geef een formule voor de drie afgeleide functies.
Hieronder staat de grafiek van een functie, die we noemen.
Een tweede functie ontstaat uit
door bij elke uitvoer van het getal op te tellen.
In formulevorm: .
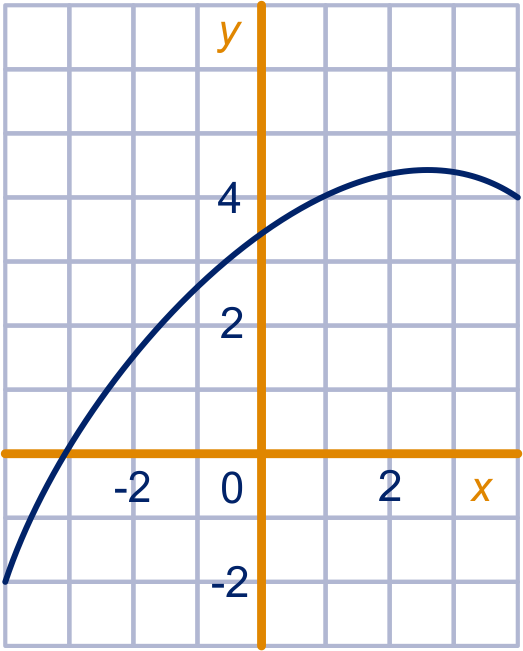
Hoe groot is ? En ?
Stel dat je de grafiek van bij de grafiek van zou tekenen.
Hoe komt de grafiek van ten opzichte van de grafiek van te liggen?
De helling van de grafiek van in het punt met is , ofwel .
Ga na of dat ongeveer klopt.
Hoe groot is de helling van de grafiek van in het punt met
?
Ofwel: hoe groot is ?
Op aarde vallen voorwerpen sneller dan op de maan. Als we op aarde een steen laten vallen (met beginsnelheid ) valt hij in seconden meter. Op de maan valt een steen in seconden maar meter. We fantaseren er nog ene planeet bij, Loekie genaamd, waar een vallende steen in seconden precies meter aflegt.

Hoeveel meter legt een vallende steen af in seconden op Loeki, op Aarde en op Maan?
Na seconden valt de steen op Loekie met een snelheid van m/s.
Hoe snel valt de steen dan op Aarde? En op Maan?
De snelheid waarmee de steen valt na seconden vinden we door de functie te differentiëren.
Wat is de formule voor de snelheid dus voor de planeet Loeki? En voor Aarde en Maan?

Hiernaast staat nogmaals de grafiek van de functie
uit opgave 54.
Een derde functie ontstaat uit
door elke uitvoer van met
te vermenigvuldigen.
In formulevorm: .
Hoe groot is ? En ?
Stel dat je de grafiek van bij de grafiek van zou tekenen.
Hoe komt de grafiek van ten opzichte van de grafiek van te liggen?
De helling van de grafiek van in het punt met is , ofwel: .
Hoe groot is de helling van de grafiek van in het punt met
?
Ofwel: hoe groot is ?
Conclusie
Als je een functie met vermenigvuldigt,
wordt zijn grafiek met factor verticaal opgerekt,
wordt zijn helling overal keer zo groot
en wordt de afgeleide functie met vermenigvuldigd.
En dat geldt net zo voor andere getallen dan .
In functienotatie:
Als , voor een constante
, dan
.
De afgeleide functie van
is .
De afgeleide functie van
is dan .
Differentieer de volgende functies.
Differentieer:
Differentieer:
Van een functie is de afgeleide functie gegeven:
.
Waarom zijn er verschillende mogelijkheden voor deze functie ? Geef enkele mogelijkheden.
De grafiek van de functie gaat door het punt . De afgeleide functie van is: .
Geef een formule voor .
De grafiek van de functie gaat door het punt . De afgeleide functie van is: .
Geef een formule voor .
Gegeven is de functie .
Teken op de GR de grafiek van deze functie. Kies een geschikt window.
is het punt op de grafiek met -coördinaat .
Teken de raaklijn aan de grafiek in punt .
Stel langs algebraïsche weg een vergelijking op van deze raaklijn.
Deze raaklijn snijdt de -as in een zeker punt. Er is nog een raaklijn aan de grafiek die door dat punt gaat.
Geef een formule voor die raaklijn.
Controleer je antwoord met de GR.
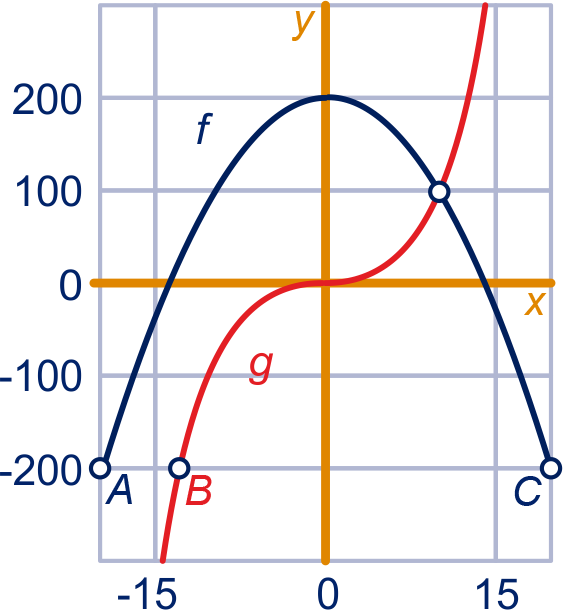
Hiernaast staan de grafieken van de functies en .
Bepaal met de GR (met intersect) de coördinaten van het snijpunt .
Controleer je antwoord met een berekening.
Stel langs algebraïsche weg een vergelijking op van de raaklijn in aan de grafiek van
.
Ook van de raaklijn in aan de grafiek van .
De lijn snijdt de grafieken in de punten , en .
Bereken exact de coördinaten van deze punten.
Is de grafiek van steiler in punt dan de grafiek van in punt , of juist omgekeerd?
