Oppervlakte van de vier driehoeken is:
.
Oppervlakte kleine vierkant is: .
Dus:
. Haakjes wegwerken geeft het gewenste resultaat.
Een hoek is de som van de twee scherpe hoeken van de een rechthoekige driehoek, dus .
De oppervlakte is .
, dus
Noem de lengte van de zwaartelijn . Pas de
cosinusregel toe.
, dus
.
We passen de sinusregel toe in driehoek .
, dus
,
dus .
,
dus .
De oppervlakte is .
We passen de cosinusregel toe in driehoek .
, dus:
.
Pas de cosinusregel toe.
, dus
, dus
.
De oppervlakte is .
, dan
oppervlakte driehoek is en
oppervlakte driehoek is .
Oppervlakte driehoek en
oppervlakte driehoek is samen
oppervlakte driehoek , dus
, dus
.
De projectie van op lijn noemen we . Dan is driehoek een -- -graden driehoek, dus .
Noem die hoek , dan , dus . De GR geeft: , dus de gevraagde hoek is: graden.
We passen nu de sinusregel toe.
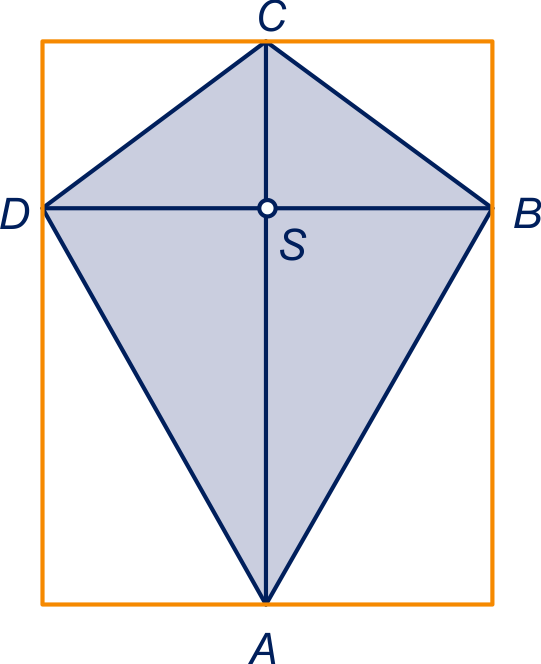
Nee, de oppervlakte van de vlieger is de helft van de oppervlakte van de rechthoek, zie figuur, dus .
en .
Hoek is recht als de stelling van Pythagoras in driehoek geldt, dus als: , dus als of .
Neem bijvoorbeeld cm als eenheid.
Teken een halve lijn met beginpunt .
Teken een halve lijn met beginpunt die een hoek van
maakt met de al getekende halve lijn .
Teken hierop het punt .
Teken een cirkel met middelpunt en straal . Deze snijdt
de halve lijn in twee punten. Elk van deze punten kan
zijn.
Pas de sinusregel toe in driehoek .
geeft:
, dus
.
De GR geeft: , dus
of
.
Dan is en
. We passen de sinusregel toe.
geeft:
, dus
.
Dan is en
. We passen de sinusregel toe.
geeft:
, dus
.
We passen de cosinusregel toe.
, hieruit volgt:
.
Pas de cosinusregel toe in driehoek .
, dus
.
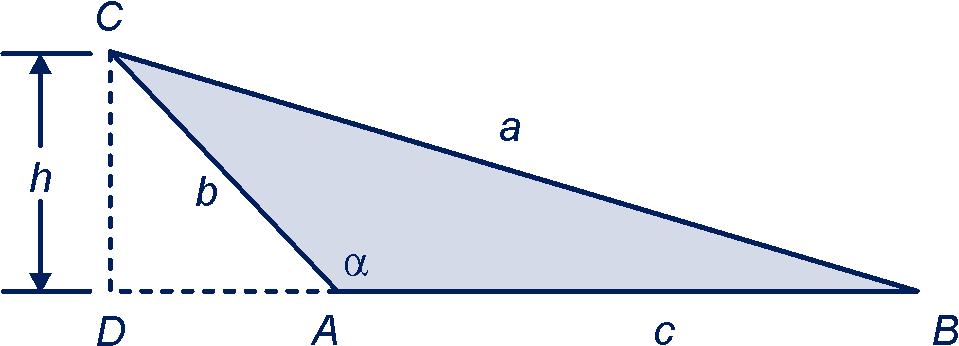
Hoek noemen we . Er geldt: . Verder: (want , dus .
, haakjes wegwerken geeft:
, dus
.
wordt:
, dus en
, dus
en
.
Dit laatste geldt in een driehoek
waarin hoek recht is.
, dit is de stelling van Pythagoras.
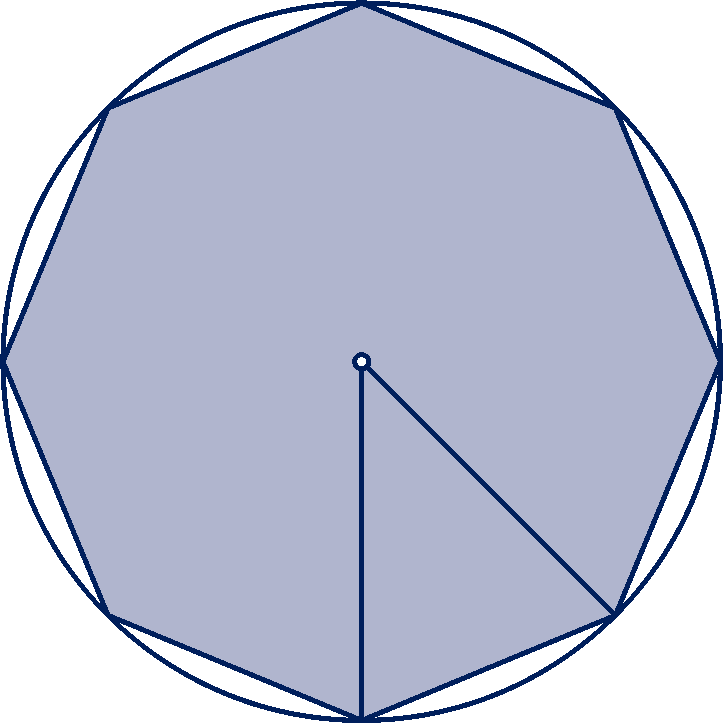
Noem de straal van de cirkel .
De achthoek is te verdelen in acht gelijkbenige driehoeken met twee zijden van lengte
en een hoek van
tussen die zijden, zie de figuur.
De oppervlakte van de achthoek is dus:
, dus
, dus .
Noem de zijde .
Pas de sinusregel toe in de driehoek met als hoekpunten het middelpunt van de cirkel en twee hoekpunten op het uiteinde van een zijde.
In die driehoek heb je twee hoeken van
en één van .
Je krijgt: , dus
.
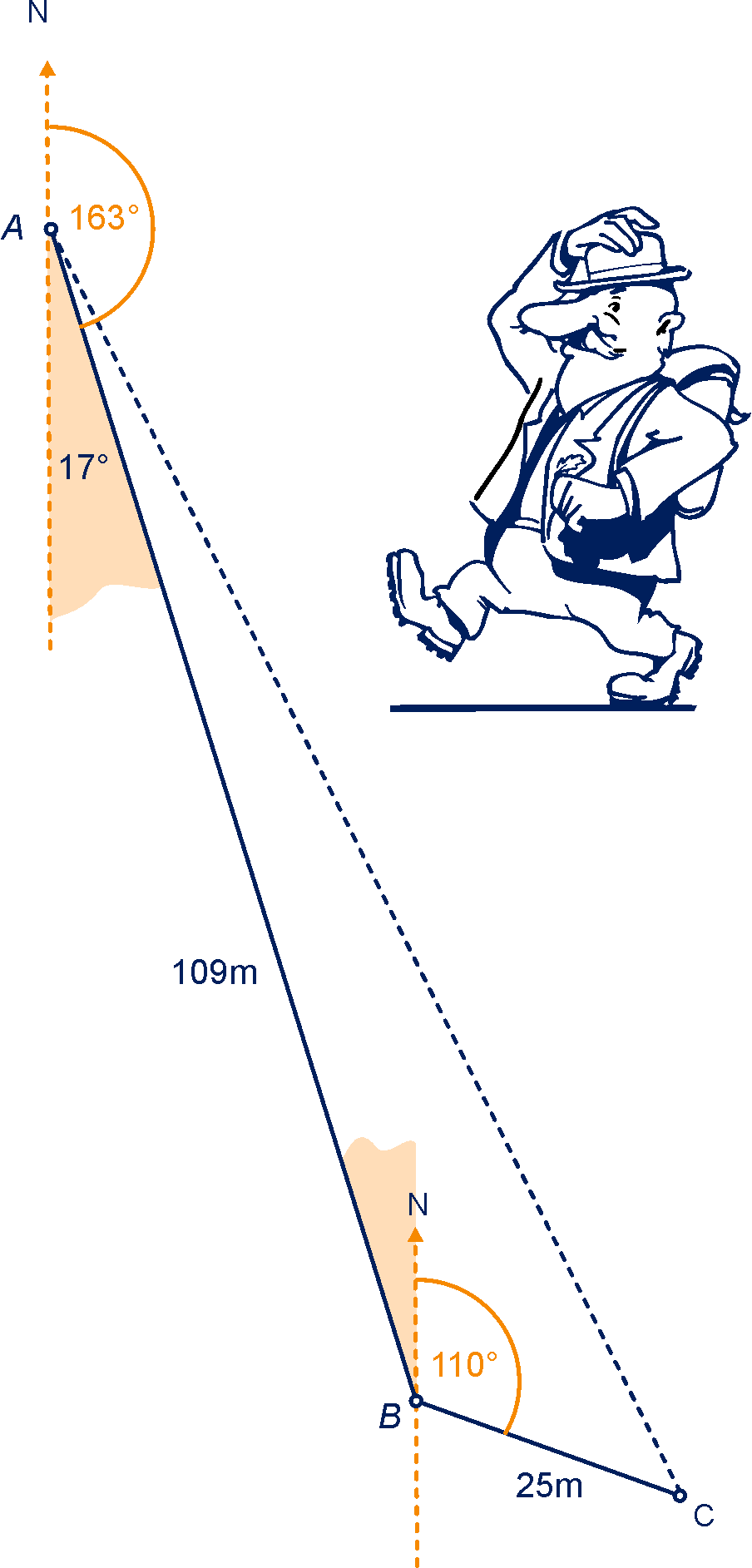
De twee okerkleurige hoeken zijn even groot (Z-hoeken). Dus in driehoek
geldt: ,
,
.
We passen de cosinusregel
toe.
Invullen geeft:
, dus
.
Nu de sinusregel toepassen:
geeft ,
de koershoek is .
(NB zoals steeds: .)
We berekenen de zijden van de driehoek.
,
en
.
Pas de cosinusregel toe.
Invullen geeft:
, dus
, dus
.
,
en
.
Hoek is recht
⇔
⇔
⇔ .
Zie de figuur.
,
,
,
,
, dus
, dus
en
de afstand tot Adam is
mijl.
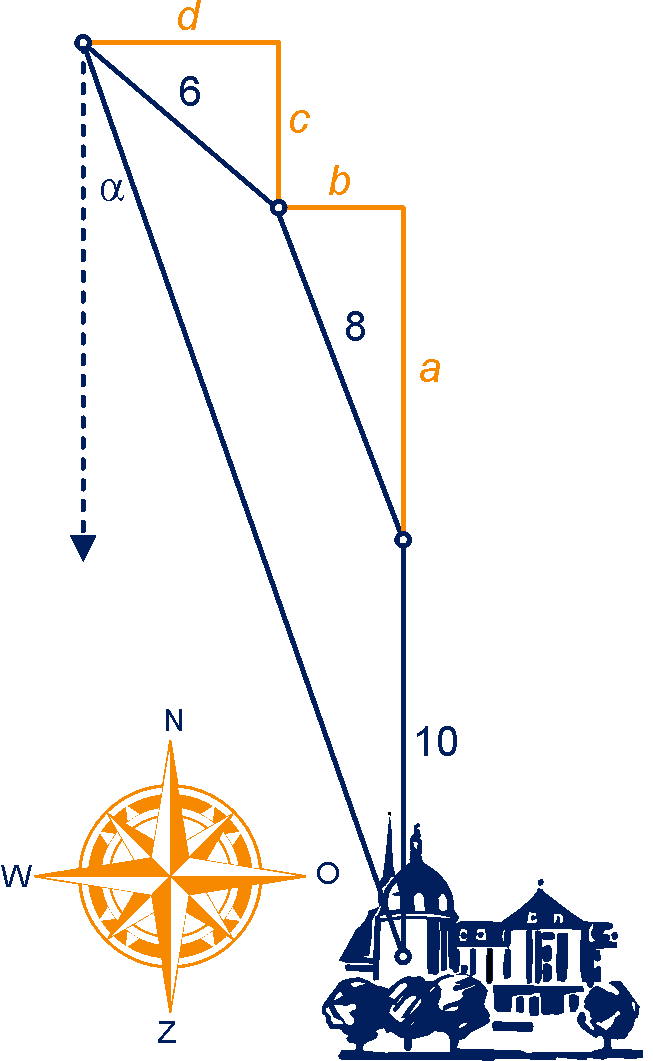
figuur bij opgave 16
|
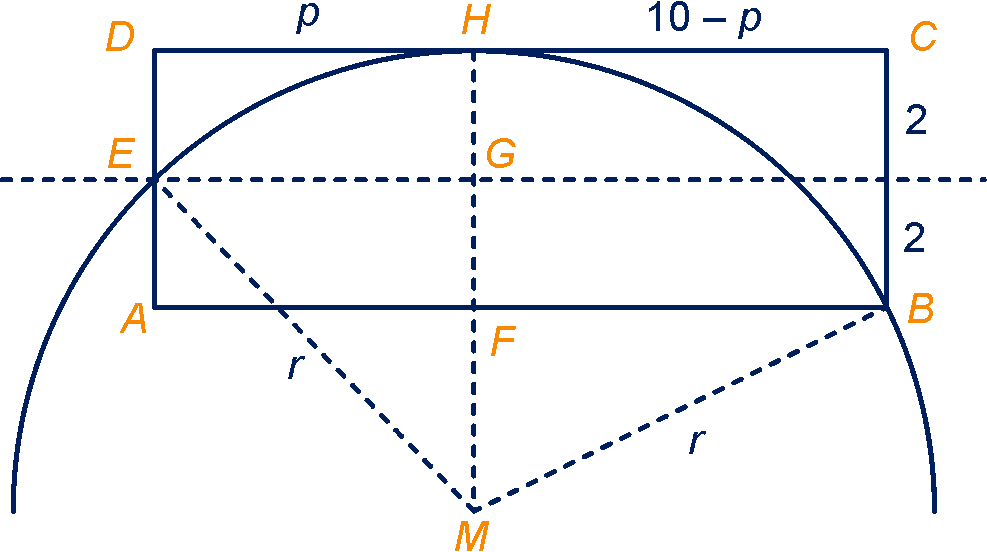
figuur bij opgave 17
|
,
en
.
Stelling van Pythagoras geeft:
.
Dus , delen door geeft het gewenste resultaat.
Het tegengestelde nemen levert:
.
, dus
en dan
(invullen in )
.
Teken nu een rechthoek van
bij .
Teken op
van op . Teken een lijn door
loodrecht op . Teken hierop op afstand
van .
Je kunt nu de cirkelboog tekenen.
Spiegel in lijn , dat wordt het middelpunt voor de andere cirkelboog.
Pas de cosinusregel
in driehoek toe:
Worteltrekken geeft:
.
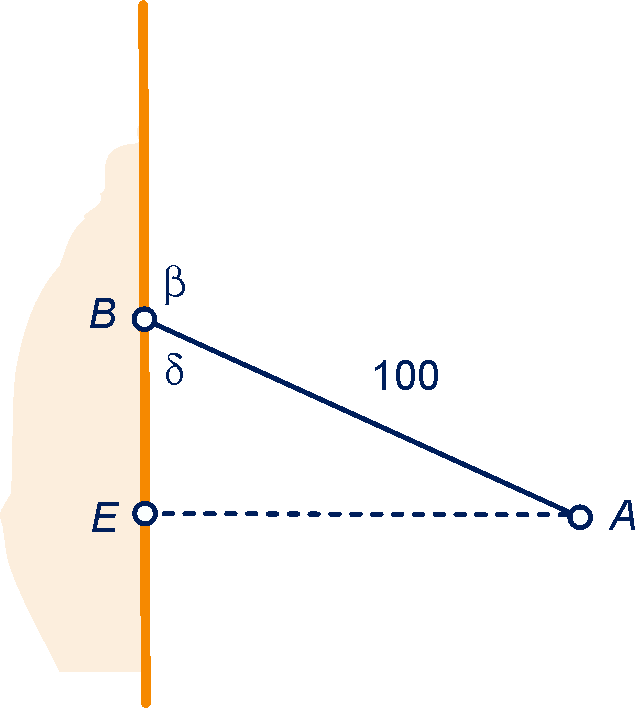
In dit geval is , dus gebruikmakend van a vind je: , kwadrateren geeft: , dus .
In de tekening op de volgende bladzijde is het punt op de muur op dezelfde hoogte als .
, dus
en
.
De hoogte van is nu cm.
Het westelijke stuk is km, het noordelijk stuk is km, samen is dat: km, dus het verschil is: km, dus km.
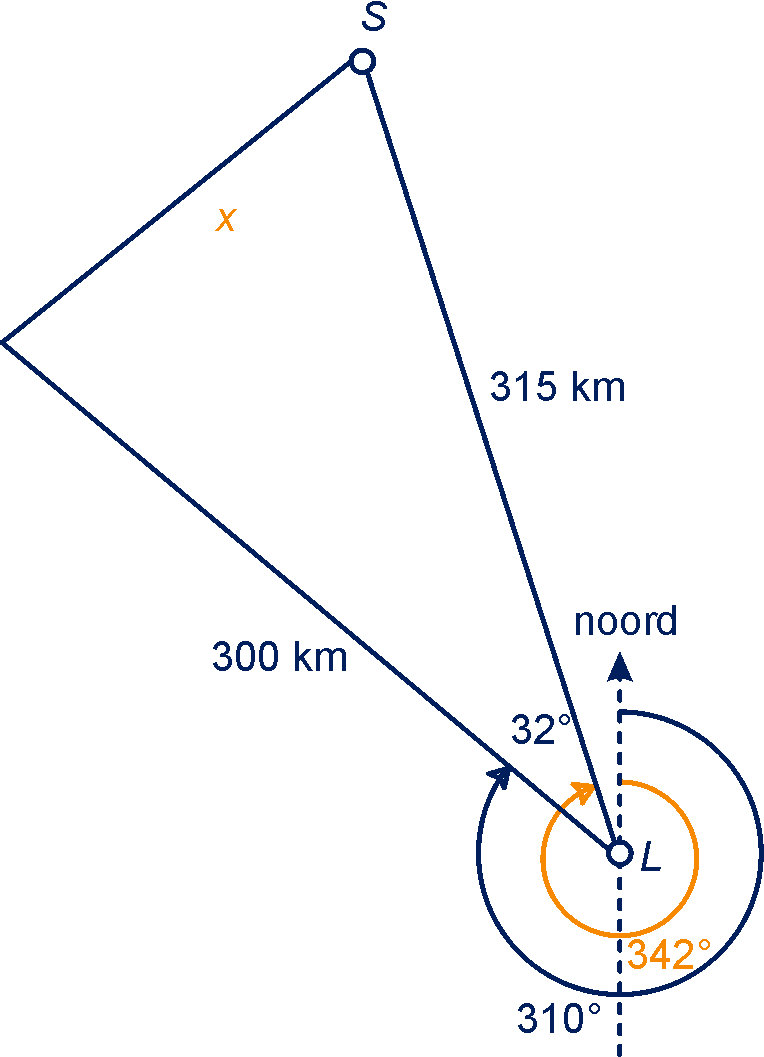
Pas de cosinusregel toe in de driehoek, zie plaatje.
dus .
De lengte van de vliegroute is dus km.
, dus de route zou met verkort kunnen worden.
De zijden van de vierkanten zijn en .
De oppervlakte van linker driehoek is: .
De oppervlakte van de rechter driehoek is hetzelfde want .
Eén van de stukken is rechthoekszijde van een rechthoekige gelijkbenige driehoek met schuine zijde
, heeft dus lengte .
Het andere stuk heeft lengte .
