Snijpunten van rechte lijnen.

Gegeven zijn de lijnen met vergelijking $y = 3 x + 4$ en $y = ‐ 2 x + 1$ .
In het snijpunt van deze twee lijnen zijn de $y$ -coördinaten voor een bepaalde waarde van $x$ gelijk aan elkaar.

Stel een vergelijking op om de $x$ -coördinaat van het snijpunt uit te rekenen.
Los deze vergelijking exact op.

Wat zijn dus de coördinaten van het snijpunt?

Bereken exact het snijpunt van de twee lijnen met vergelijking $y = ‐ 2 x - 7$ en $y = 5 x + 3$ .

Om het snijpunt van de lijnen met vergelijking $y = \frac{3}{4} x + 1$ en $y = \frac{2}{3} x + \frac{1}{2}$ op te lossen krijg je de vergelijking $\frac{3}{4} x + 1 = \frac{2}{3} x + \frac{1}{2}$ .
Om deze op te lossen moet je veel met breuken rekenen. Het is dan handiger om de hele vergelijking (dus alle termen van de vergelijking) met een getal te vermenigvuldigen, zodat de breuken verdwijnen.

Met welk getal kun je deze vergelijking het beste vermenigvuldigen?
Doe dit en los de vergelijking verder op.
Wat zijn de coördinaten van het snijpunt?

Bereken zo ook de exacte coördinaten van het snijpunt van de lijnen met vergelijking $y = ‐ \frac{1}{5} x - \frac{1}{4}$ en $y = ‐ \frac{1}{2} x + 2$ .

Gegeven zijn de lijnen met vergelijking $y = 3 x + 2$ en $3 x - 4 y = 10$ .
Om het snijpunt van deze twee lijnen te berekenen kun je de tweede vergelijking eerst omzetten in de vorm $y = ...$ en dan het snijpunt uitrekenen door ze aan elkaar gelijk te stellen.

Bereken op deze manier de exacte coördinaten van het snijpunt.

In plaats van de tweede vergelijking eerst om te schrijven, kun je de eerste vergelijking ook substitueren (of 'invullen') in de andere vergelijking:
Je krijgt dan $3 x - 4 (3 x + 2) = 10$ .

Los deze vergelijking verder op.
Wat is het voordeel van deze methode ten opzichte van de eerste methode?

Bereken met deze substitutie-methode de coördinaten van het snijpunt van de volgende twee lijnen:
$y = ‐ 2 x - 3$ en $‐ 2 x + 3 y = 15$ .

Soms heb je twee lijnen met vergelijkingen in de vorm $a x + b y = c$ .
Om dan het snijpunt van de twee lijnen uit te rekenen heb je de volgende mogelijkheden:

Beide vergelijkingen omzetten in de vorm $y = ...$ en dan aan elkaar gelijkstellen.
Eén van beide vergelijkingen omzetten in de vorm $y = ...$ (of $x = ...$ ) en deze dan in de andere substitueren.

Gegeven zijn de twee lijnen met vergelijking $3 x - 4 y = 10$ en $‐ x + 3 y = 15$ .

Bereken exact het snijpunt van de twee lijnen. Kies zelf een werkwijze.

Bereken de exacte coördinaten van het snijpunt van de lijnen met vergelijking $3 x + 2 y = 6$ en $5 x + 4 y = 8$ .

Lijnenbundels

Gegeven is voor elke waarde van $a$ lijn $k_{a}$ met vergelijking $y = a (x - 1) + 3$ .
Voor elke waarde van $a$ krijg je een andere lijn.
Als je bijvoorbeeld $a = 2$ neemt, krijg je de lijn $k_{2}$ met vergelijking $y = 2 (x - 1) + 3$ , ofwel $y = 2 x + 1$ .
En $a = ‐ 3$ geeft lijn $k_{‐ 3}$ : $y = ‐ 3 (x - 1) + 3 = ‐ 3 x + 6$ .
In de figuur hieronder staan voor negen verschillende waarden van $a$ de grafiek van $k_{a}$ getekend.

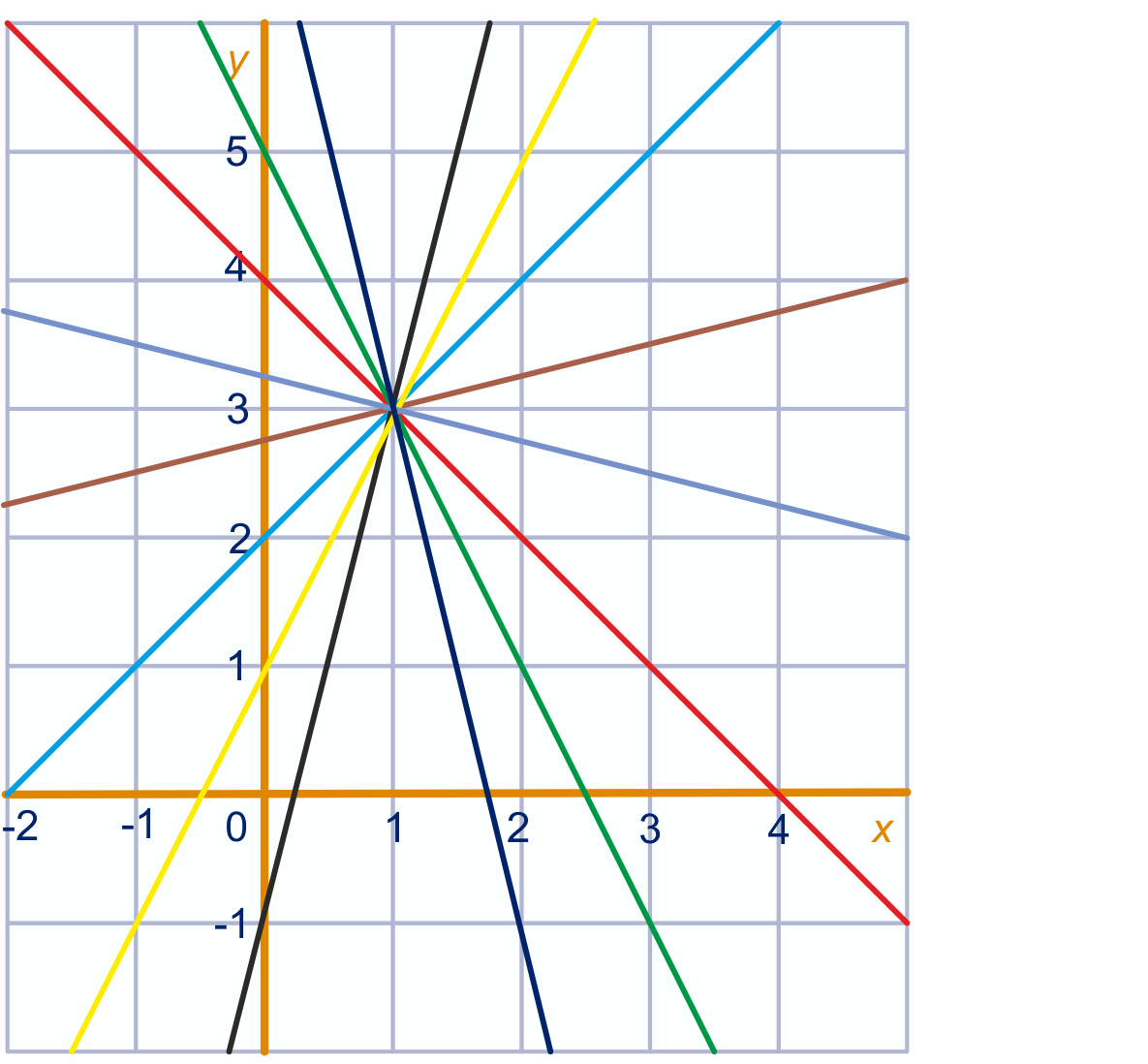
Je ziet dat je een zogenaamde lijnenbundel of lijnenwaaier krijgt:
lijn $k_{a}$ gaat voor elke waarde van $a$ door het punt $(1,3)$ , met telkens een andere richtingscoëfficiënt.

Voorbeeld:

Voor welke waarde van $a$ gaat lijn $k_{a}$ door de oorsprong?

Oplossing
Vul punt $(0,0)$ in de vergelijking van $k_{a}$ in.
Je krijg $0 = a \cdot (0 - 1) + 3$ , ofwel $‐ a + 3 = 0$ . Dus $a = 3$ .

Gegeven is voor elke waarde van $a$ lijn $k_{a}$ met vergelijking $y = a x + 7$ .

Welk punt ligt op lijn $k_{a}$ voor elke waarde van $a$ ?

Bereken exact voor welke waarde van $a$ lijn $k_{a}$ door het punt $(10, ‐ 2)$ gaat.

Lijn $m$ heeft vergelijking $y = 3 x - 2$ .

Voor welke waarde van $a$ hebben lijnen $k_{a}$ en $m$ geen punten gemeenschappelijk?

Het snijpunt van $k_{a}$ en $m$ ligt op de $x$ -as. Bereken exact de waarde van $a$ .

Gegeven is voor elke waarde van $a$ lijn $m_{a}$ met vergelijking $y = a (x + 5) + 3$ .

Welk punt ligt op lijn $m_{a}$ voor elke waarde van $a$ ?

(hint)

Teken de lijn voor enkele waarden van $a$ .

Bereken exact voor welke waarde van $a$ lijn $m_{a}$ door het punt $(10, ‐ 2)$ gaat.

Bereken exact voor welke waarden van $a$ lijn $m_{a}$ de $y$ -as op afstand $4$ van de oorsprong snijdt.
(Let op: er zijn twee waarden van $a$ .)

Gegeven is lijn $n_{a}$ met vergelijking $a x + 3 y = 7$ .

Bereken voor welke waarde van $a$ punt $(2,5)$ op lijn $n_{a}$ ligt.

Onderzoek of er nu ook een punt is die voor elke waarde van $a$ op lijn $n_{a}$ ligt.

Neem $a = 2$ . Bereken de richtingscoëfficiënt van $n_{2}$ .

Bereken voor welke waarde van $a$ lijn $n_{a}$ richtingscoëfficiënt $‐ 5$ heeft.

Bereken exact voor welke waarde van $a$ lijn $n_{a}$ evenwijdig is aan de lijn met vergelijking $3 x - 2 y = 7$ .

Punten op lijnen

Gegeven zijn de punten $A (p,5)$ , $B (2, p)$ en $C (p + 3, p - 8)$ .

Bereken $p$ als punt $A$ op de lijn met vergelijking $y = 3 x - 7$ ligt.

Bereken exact voor welke waarde van $p$ lijn $A B$ richtingscoëfficiënt $1$ heeft.

Bereken exact voor welke waarde van $p$ lijn $B C$ richtingscoëfficiënt $‐ 1$ heeft.

Bereken exact voor welke waarden van $p$ lijnen $A B$ en $B C$ dezelfde richtingscoëfficiënt hebben.

Gegeven zijn voor elke waarde van $a$ de punten $P (1,2)$ en $Q (a,2 a)$ .

Neem $a = 3$ en bereken de richtingscoëfficiënt van de lijn $P Q$ .

Bereken ook de richtingscoëfficiënt als $a = 5$ , als $a = ‐ 2$ en als $a = 6,2$ .

In opgave 64 kreeg je vier keer hetzelfde antwoord (als je die opgave goed gemaakt hebt). In opgave 65 gaan we dat begrijpen.

Voorbeeld:

$\frac{3 x - 3 y}{2 x - 2 y} = \frac{3 (x - y)}{2 (x - y)} = \frac{3}{2} = 1 \frac{1}{2}$

Vereenvoudig zo ook:

\frac{8 x + 4 y}{6 x + 3 y}

\frac{4 - 2 p}{10 - 5 p}

\frac{k - 3}{9 - 3 k}

We keren terug naar de lijn $P Q$ in opgave 64.

Laat zien dat de richtingscoëfficiënt van lijn $P Q$ voor elke waarde van $a \neq 1$ gelijk is aan $\frac{2 a - 2}{a - 1}$ .
Laat vervolgens langs algebraïsche weg zien dat voor elk getal $a \neq 1$ de richtingscoëfficiënt $2$ is.

Waarom is er bij vraag b vermeld dat $a$ ongelijk $1$ is?

Gegeven zijn de punten $A (p, q)$ en $B (q, p)$ .

Neem $p = 3$ en $q = 5$ en bereken de richtingscoëfficiënt van de lijn $A B$ .

Bereken ook de richtingscoëfficiënt als $p = ‐ 3$ en $q = 10$ .
En als $p = ‐ 1 \frac{1}{2}$ en $q = ‐ 6$ .

Laat langs algebraïsche weg zien dat voor alle getallen $p$ en $q$ ( $p \neq q$ ), de richtingscoëfficiënt $‐ 1$ is.

Waarom is er bij vraag c vermeld dat $p$ en $q$ niet gelijk aan elkaar zijn?

Gegeven zijn de punten $A (p, p^{2})$ en $B (q, q^{2})$ .

Neem $p = 3$ en $q = 5$ en bereken de richtingscoëfficiënt van de lijn $A B$ .

Bereken ook de richtingscoëfficiënt als $p = ‐ 3$ en $q = 10$ .
En ook als $p = 2$ en $q = ‐ 8$ .

Laat langs algebraïsche weg zien dat voor alle getallen $p$ en $q$ ( $p \neq q$ ), de richtingscoëfficiënt $p + q$ is.

Waarom is er bij vraag c vermeld dat $p$ en $q$ niet gelijk aan elkaar zijn?

Gegeven zijn de punten $A (p,5)$ , $B (2, p)$ en $C (2 p,4 p - 1)$ .

Bereken exact voor welke waarde van $p$ de punten $A$ , $B$ en $C$ op een rechte lijn liggen.