Hiernaast zie je de bevolkingspiramide van Nederland op 1 januari 2022, gebaseerd op CBS-gegevens.
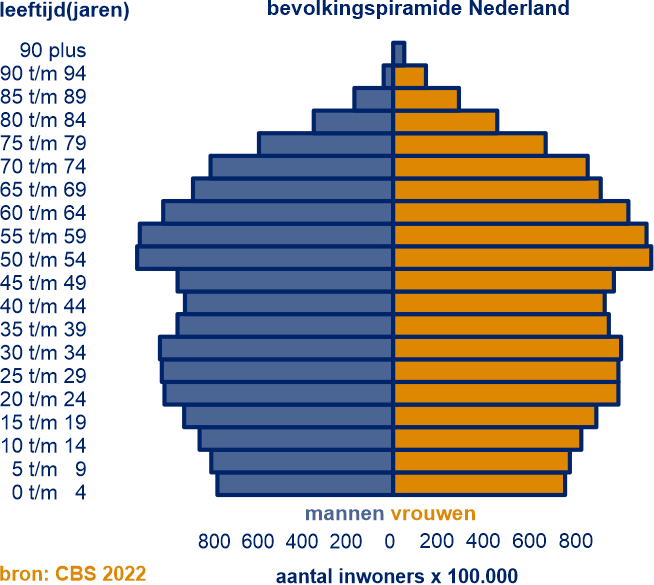
Vergelijk de mannen (links) met de vrouwen, voor de leeftijden 80 en hoger.
Wat valt je op?
In de tachtiger jaren verkeerde Nederland in een laagconjunctuur (economisch zwakke periode).
Hoe zie je dat aan de piramide?
Er worden ongeveer evenveel jongens als meisjes geboren, maar niet precies evenveel.
Worden er meer jongens of meer meisjes geboren?
Het plaatje wordt een bevolkingspiramide genoemd.
Kun je het woord piramide verklaren?
De bevolking in Nederland
"vergrijst"
. Wat betekent dat?
Hoe zal de bevolkingspiramide in de toekomst veranderen?
De modale leeftijd is de leeftijd die het vaakst voorkomt.
Welke is dat in 2022?

Het plaatje hiernaast komt uit het boekje Nederland in cijfers van het CBS editie 2023. Het gaat over het inkomen van de werkenden dat jaar in Nederland. De werkenden zijn ingedeeld in klassen van breedte € 10.000:
minder dan € 10.000, € 10.000 - € 20.000, € 20.000 - € 30.000
enzovoort.
Hoeveel procent van de werkenden verdiende meer dan € 100.000. Rond je antwoord af op één decimaal.
We bekijken de groep werkenden die minder dan € 100.000 verdienen.
Bereken het gemiddelde inkomen van zo'n werkende. Werk met klassenmiddens.
Wat is de modale inkomensklasse?
Volgens het CBS is het gemiddelde inkomen van werkenden € 46.900.
Bereken met behulp van je antwoord op b hiermee het gemiddelde inkomen van de werkenden die meer dan € 100.000 krijgen.
Scholieren besteden hun zakgeld voornamelijk aan snacks, drank, kleding en natuurlijk het mobieltje.
Hoe komt de jeugd aan haar geld?
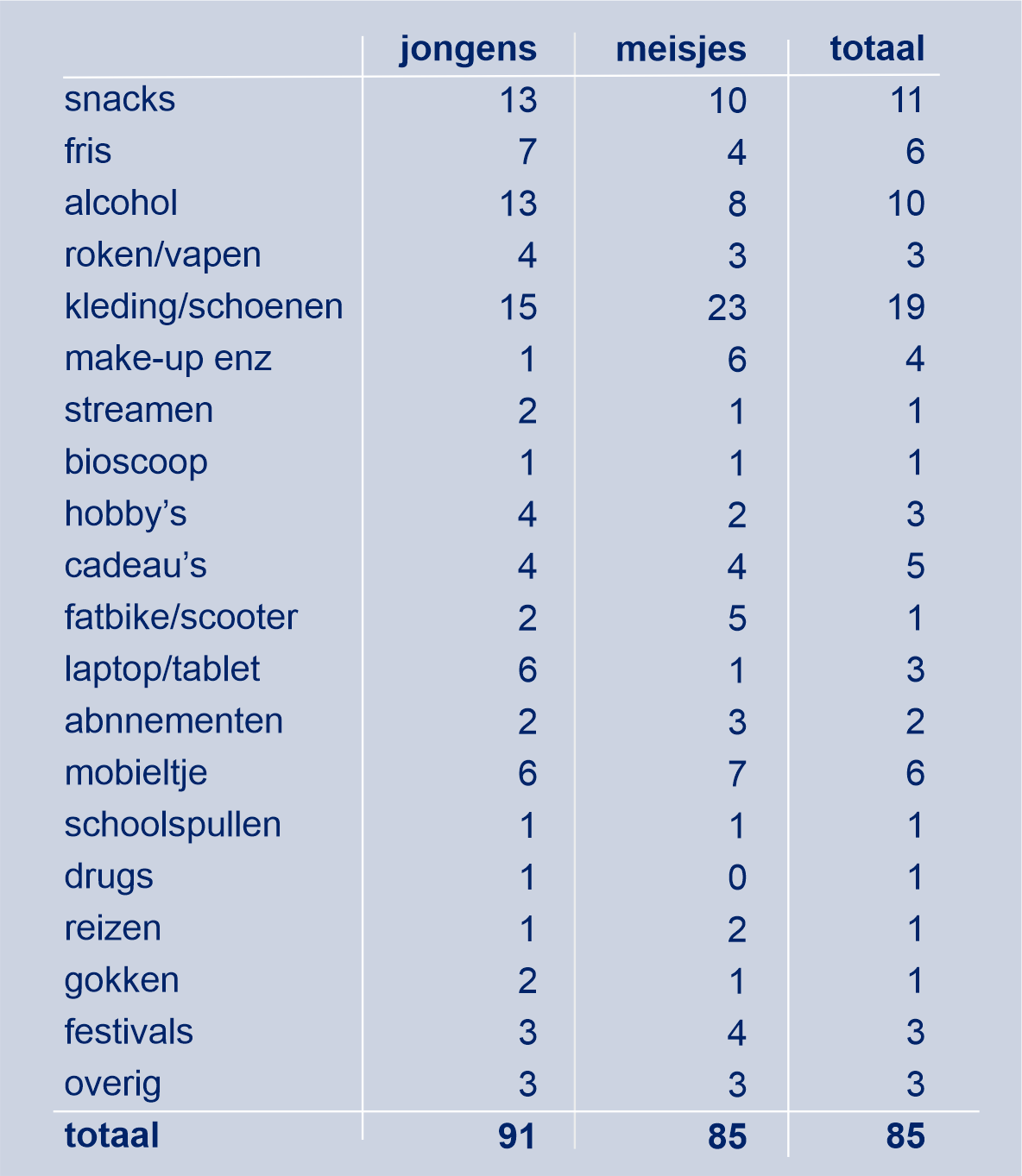
In de tabel staan de gemiddelde bedragen die scholieren per maand uitgeven. De bedragen zijn in euro's.
Aan welke dingen besteden jongens beduidend meer geld dan meisjes?
De bedragen in de kolommen jongens
en meisjes
kloppen niet allemaal precies met die in de kolom Totaal
.
Hoe komt dat?
Hoeveel procent van hun geld wordt door meisjes aan kleding en schoenen besteed?
Om meer overzicht te krijgen helpt het items samen te nemen. De samengenomen items noemen we een
sector.
We bekijken de volgende sectoren:
| consumpties: | snacks + fris + alcohol + roken/vapen + drugs |
| verzorging: | kleding/schoenen + make-up enz |
| vrije tijd: | streamen + hobby's + tijdschriften + abonnementen + bioscoop |
| sociaal: | cadeaus + fatbike/scooter + laptop + mobiel + reizen + festivals |
| overig: | gokken + overig |
Bereken van elke sector de totale uitgaven?
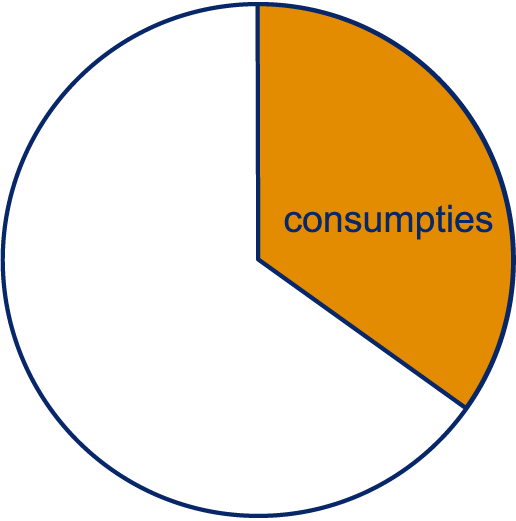
We gaan een cirkeldiagram maken voor de verdeling van de uitgaven van de jongens met deze vijf sectoren. De grootte van de sectoren is evenredig met de grootte van de uitgaven in die sector. De sector Consumpties omvat 38 euro van het totaal van 91 euro, dat is 41,8%. De sector Consumpties krijgt daarom een hoek van 41,8% van 360°, dat is ruim 150°.
Bereken de grootte van de hoeken van de andere vier sectoren.
Hiernaast is de sector consumpties af getekend.
Neem die over en maak het cirkeldiagram af.
In plaats van een cirkel te verdelen in vijf sectoren, kun je ook een staaf (een balk) verdelen in vijf stukken. Zo’n plaatje heet een staafdiagram.

Maak een staafdiagram voor de meisjes, op dezelfde schaal als voor de jongens.
De tabel van de gemiddelde bedragen die scholieren per maand uitgeven staat ook in het programma Excel op de
website van de Wageningse Methode.
Om meer overzicht te krijgen helpt het verschillende items samen te nemen.
| consumpties: | snacks + fris + alcohol + roken/vapen + drugs |
| verzorging: | kleding/schoenen + make-up enz |
| vrije tijd: | streamen + hobby's + tijdschriften + abonnementen + bioscoop |
| sociaal: | cadeaus + fatbike/scooter + laptop + mobiel + reizen + festivals |
| overig: | gokken + overig |
Maak met Excel een cirkeldiagram bij deze indeling en een staafdiagram voor de meisjes.
Gebruik Wizard grafieken, type Cirkel en Staaf.
Klas B2x van 25 leerlingen heeft een onderzoekje gedaan. Van elke leerling is zijn gewicht bepaald met een personenweegschaal. De resultaten staan hieronder opgesomd (in kg).
50, 48, 48, 58, 39, 44, 56, 42, 53, 48, 47, 41, 55, 49, 37, 54, 37, 40, 43,
48, 44, 53, 42, 46, 45.

In het plaatje zie je een liniaal. Boven de liniaal zijn de eerste drie metingen weergegeven door een stip.
Neem het plaatje over.
Geef elke meting aan met een stip.
Zodoende heb je een aardig beeld gekregen van de gewichten van de leerlingen in B2x.
De spreidingsbreedte is het verschil tussen de grootste en de kleinste gemeten waarde.
Wat is de spreidingsbreedte van het lichaamsgewicht in klas B2x?
We gaan een histogram maken bij de gewichten. Daartoe delen we de gewichten eerst in klassen in.
In de eerste klasse komen de gewichten van 35 tot en met 39.
In de tweede klasse de gewichten van 40 tot en met 44. Enzovoort. De grenzen van de klassen verschillen dus 5 kg.
We zeggen dat de
klassenbreedte 5 kg is.

Bepaal de frequentie van elke klasse. Dat is het aantal gewichten die in de klasse vallen.
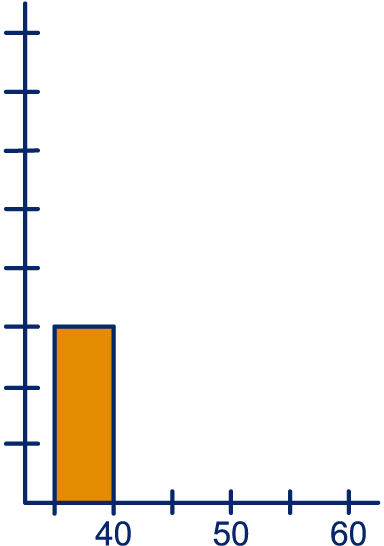
Wat is de modale klasse? Dat is de klasse met de meeste leerlingen.
Teken bij de tabel een histogram. De eerste balk is al getekend.
Klas B2x van 25 leerlingen heeft een onderzoekje gedaan. Van elke leerling is zijn gewicht bepaald met een personenweegschaal.
De resultaten staan hieronder opgesomd (in kg).
50, 48, 48, 58, 39, 44, 56, 42, 53, 48, 47, 41, 55, 49, 37, 54, 37, 40, 43, 48,
44, 53, 42, 46, 45
Deze gewichten staan ook in het Excel-programma op de website van de Wageningse Methode.
Sorteer de gewichten op volgorde.
Maak een histogram met behulp van de Wizard grafieken, grafiektype Kolom.
Frequentie komt van het Latijnse woord frequentia wat talrijkheid betekent.
Histos is het Griekse woord voor mast; gramma is het Griekse woord voor teken.
Histogram zou je dus kunnen vertalen met tekening met masten.
Modus betekent letterlijk norm: de modus is de vaakst voorkomende waarde.
Spreidingsbreedte is het verschil tussen de grootste en kleinste gemeten waarde.
Het vak statistiek is in het begin van de negentiende eeuw ontstaan. Het heette toen nog statenkunde. Oorspronkelijk behandelde het vak allerlei feiten over de staat, zoals het klimaat, de bevolking, het leger en de handel. Zaken dus die we nu tot aardrijkskunde, geschiedenis of economie rekenen. Toen werd er ook nauwelijks gerekend bij de statistiek. Tegenwoordig is dat wel het geval.
