9.2 Gehele getallen optellen en aftrekken (1) >

Natuurlijke getallen

De natuurlijke getallen zijn de getallen $0, 1, 2, 3, \dots, 387, 388, \dots$ .
Die puntjes betekenen enzovoorts.

Wat is het kleinste natuurlijke getal?

Wat is het grootste natuurlijke getal?

We kunnen een plaatje maken van de natuurlijke getallen, door ze op onderling gelijke afstand aan te geven op een rechte lijn.

Zo'n plaatje noemen we een getallenlijn. Eigenlijk is het maar een stukje van de getallenlijn. Je kunt je vast wel voorstellen hoe de getallenlijn verder loopt.

Is het mogelijk om de getallenlijn helemaal te tekenen?

Op de getallenlijn zijn met stippen de even getallen aangegeven.

Maak een zelfde soort plaatje van de drievouden.

Maak ook een plaatje van de delers van 12.

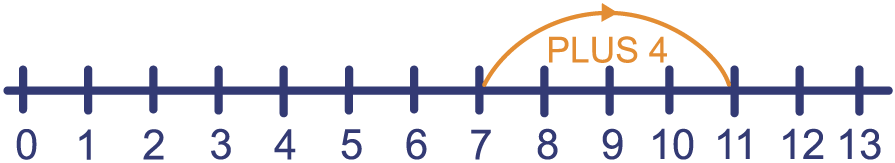
Op de getallenlijn zie je wat er gebeurt als je het getal 7 in het machientje PLUS 4 stopt: je gaat vanuit 7 vier stapjes naar rechts.
Je ziet dat $7 + 4 = 11$ .

Teken ook zo'n getallenlijn.

Teken nog drie andere pijlen die horen bij het machientje PLUS 4.

Teken op een nieuwe getallenlijn een paar pijlen die horen bij het machientje MIN 4.

Op de getallenlijn is de plaats van de getallen 0, 3 en $x$ aangegeven.
Geef op de getallenlijn op je werkblad de plaats van $x + 3$ en $x - 3$ aan.

Neem over en vul in ( $x$ is een variabele).

$7 \to PLUS 4 \to .....$	$7 \to MIN 4 \to .....$
$3 \to PLUS 4 \to .....$	$13 \to MIN 4 \to .....$
$x \to PLUS 4 \to .....$	$x + 5 \to MIN 4 \to .....$
$x + 2 \to PLUS 4 \to .....$	$..... \to MIN 4 \to x$

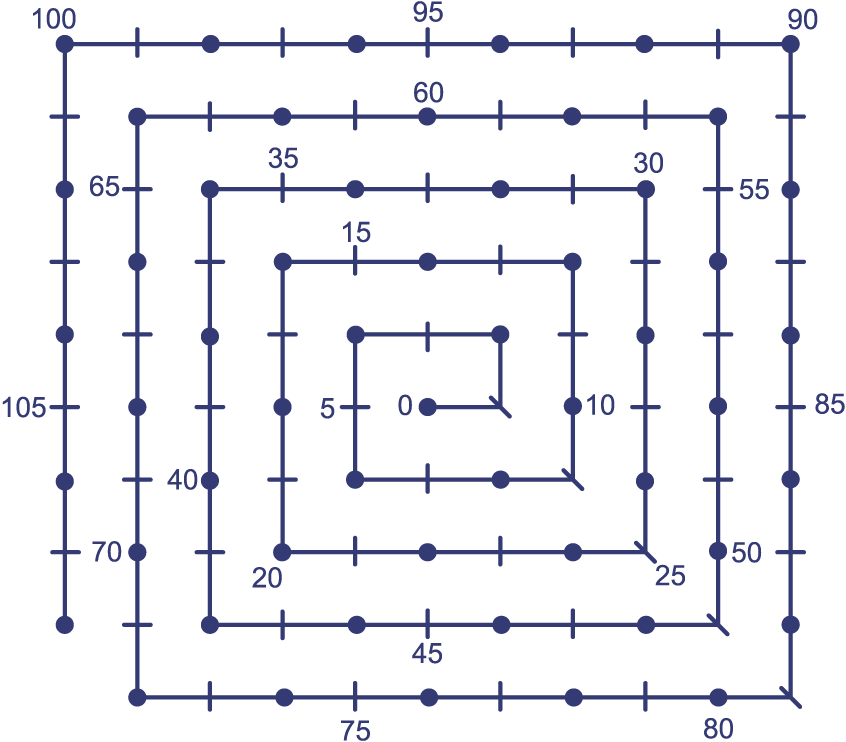
Om een groter stuk van de getallenlijn te kunnen tekenen hebben we de getallenlijn opgerold. Op de opgerolde getallenlijn zijn de even getallen met een dikke stip aangegeven.

Geef met een rode stip de kwadraten aan.

Geef met een blauwe stip de getallen aan die een vijfvoud zijn en ook even zijn.

Als het goed is heb je 0 zowel blauw als rood gekleurd.

Er is naast 0 nog een getal dat zowel blauw als rood gekleurd is. Welk getal is dat?

Als je de getallenlijn verder tekent, kom je nog meer getallen tegen die zowel blauw als rood gekleurd zijn.

Welk getal is het eerstvolgende getal dat zowel blauw als rood gekleurd wordt?

En wat is het daaropvolgende getal met deze eigenschap?

Bij het machientje MIN 4 kun je geen pijl tekenen die uit 1 vertrekt: je wilt eigenlijk vier stapjes naar links, maar na één stapje ben je al bij 0 aanbeland, en dan kun je niet verder.

In plusmachientjes kun je alle natuurlijke getallen stoppen: het machientje spuugt altijd weer een natuurlijk getal uit. Minmachientjes weten met sommige getallen geen raad: als je in het machientje MIN 4 het getal 1 stopt, slaat het op tilt. Het machientje kan geen natuurlijk getal uitspugen.

Als we de som $1 - 4$ willen uitrekenen, hebben we een probleem. We komen onder nul uit. De getallenlijn moet daarom uitgebreid worden. De getallen die er onder nul bijkomen zijn negatieve getallen.

We breiden de getallenlijn naar links uit: één stapje links van 0 zetten we het getal $‐1$ neer, twee stapjes links van 0 zetten we $‐2$ neer, enzovoorts.

De getallen $\dots, ‐4, ‐3, ‐2, ‐1, 0, 1, 2, 3, 4, \dots$ worden gehele getallen genoemd. $‐1, ‐2, ‐3 \dots$ heten negatief; $1, 2, 3 \dots$ heten positief. 0 is niet positief en ook niet negatief.

Op onze nieuwe getallenlijn kunnen we wel op alle getallen het machientje MIN 4 laten werken. Zo zie je dat $1 - 4 = ‐3$ .

We kunnen ons het getal $‐3$ ook voorstellen met blokjes. Je hebt een bak met koude en met warme blokjes. De koude blokjes zijn de negatieve getallen en de warme blokjes de positieve getallen.
Elk blokje heeft de waarde $+ 1$ of ${‐1}^{\circ} C$ .
Een koud blokje samen met een warm blokje geeft $0^{\circ} C$ , dus het getal 0.
Het getal $‐3$ betekent dat er drie koude blokjes meer in de bak zitten dan warme blokjes.

Je ziet twee bakken getekend met daarin warme en koude blokjes. In de linker bak zitten 5 warme en 8 koude blokjes. De temperatuur in deze bak is dus $‐3$ graden. In de rechter bak zitten 2 warme en 5 koude blokjes. In deze bak is de temperatuur dus ook $‐3$ graden.

Teken zelf nog twee verschillende bakken waarin de temperatuur $‐3$ graden is.

Teken ook twee verschillende bakken waarin de temperatuur 4 graden is.

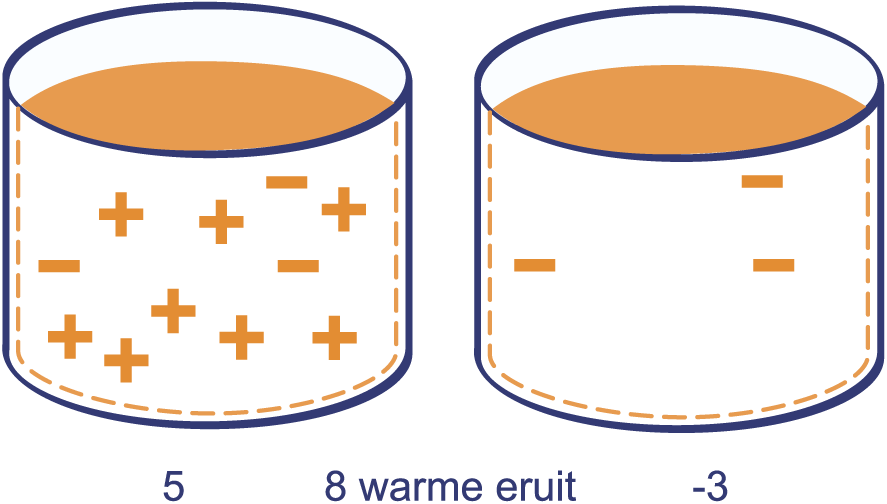
In de linker bak zitten 5 warme blokjes meer dan koude. De temperatuur in deze bak is dus 5 graden.
Als je 8 warme blokjes uit de linker bak haalt, dan daalt de temperatuur met 8 graden. De temperatuur wordt $‐3$ graden.
Bij dit verhaal hoort de som $5 - + 8 = ‐3$ .
Met behulp van de getallenlijn kun je nagaan dat $5 - 8$ ook als antwoord $‐3$ heeft.
Het blijkt dat $5 - + 8$ hetzelfde is als $5 - 8$ .

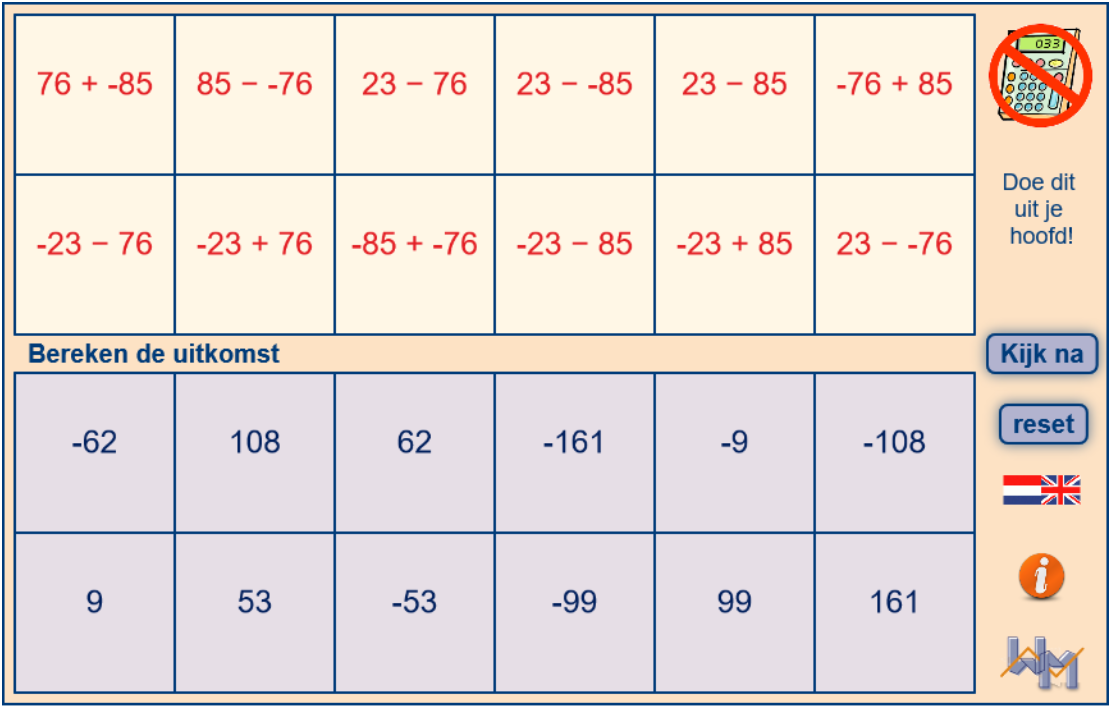
Bereken:

$8 - 17$	$13 - 27$
$12 - 17$	$16 - 27$
$28 - 17$	$24 - 27$

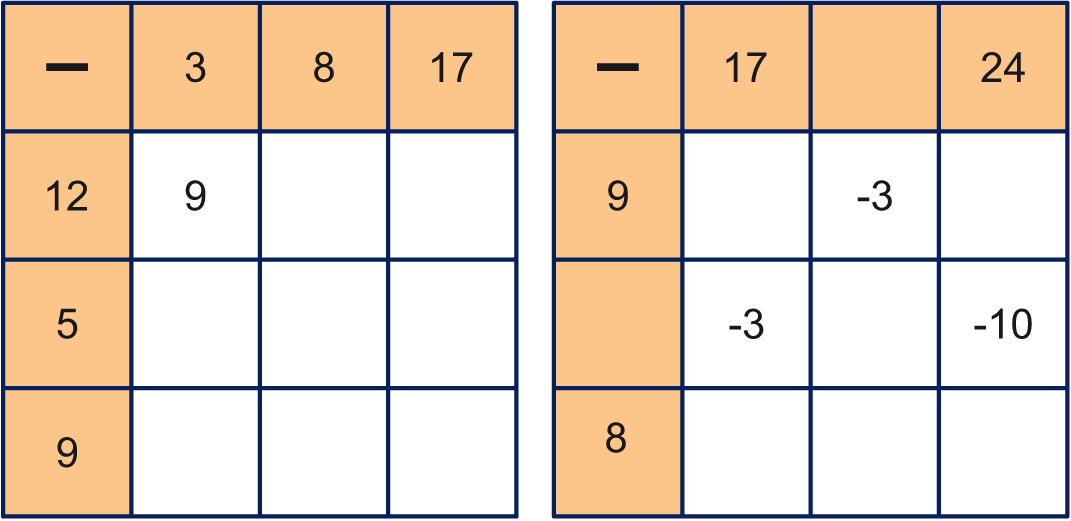
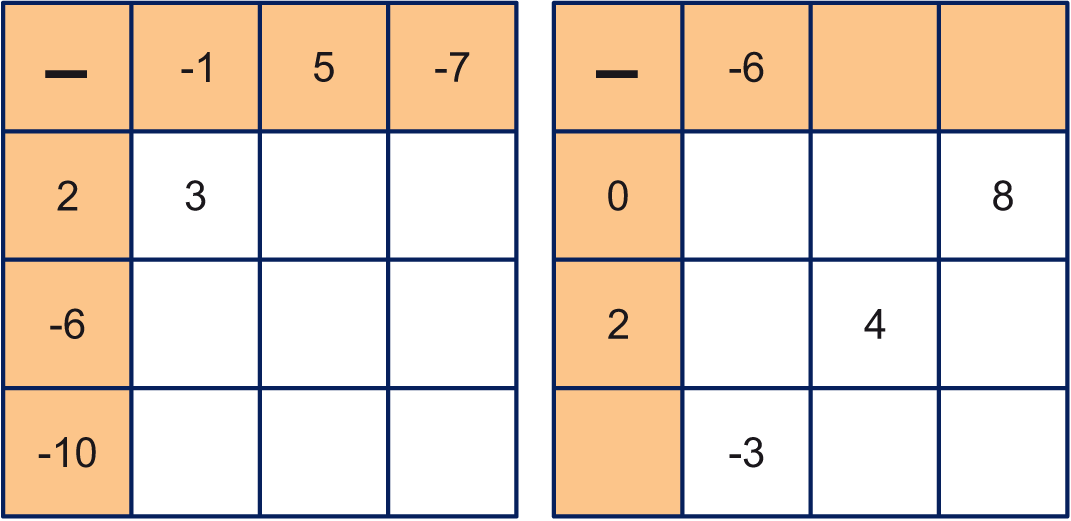
In de twee aftrektabellen moeten de drie getallen aan de bovenkant afgetrokken worden van de drie getallen aan de linker zijkant. Als voorbeeld is 3 van 12 afgetrokken: uitkomst 9.
Neem de aftrektabellen over en vul ze verder in.

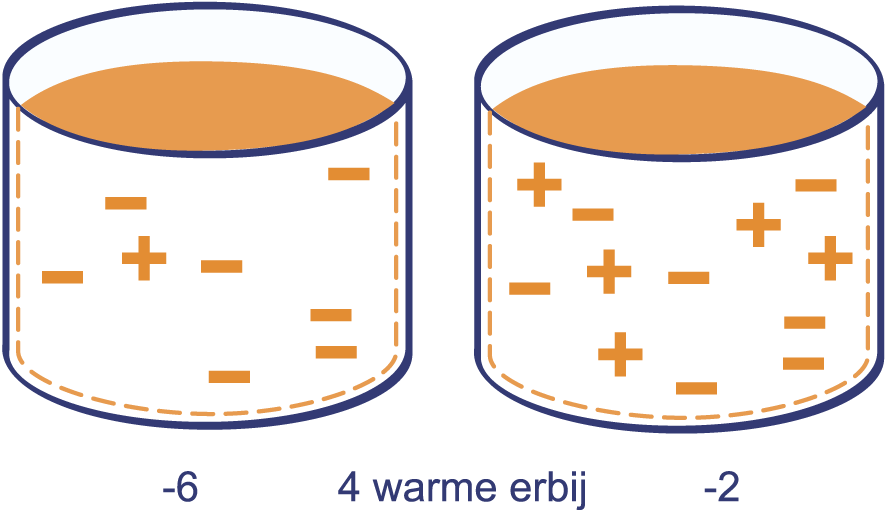
De temperatuur in de linker bak is $‐6$ graden (in deze bak zitten dus 6 koude blokjes meer dan warme). Als je 4 warme blokjes in deze bak gooit, dan stijgt de temperatuur met 4 graden. De temperatuur wordt $‐2$ graden.
Bij dit verhaal hoort de som $‐6 + + 4 = ‐2$ .
Met behulp van de getallenlijn kun je nagaan dat $‐6 + 4$ ook als antwoord $‐2$ heeft.
Het blijkt dat $‐6 + + 4$ hetzelfde is als $‐6 + 4$ .

Bereken:

$‐17 + 8$	$‐9 + 27$
$‐17 + 12$	$‐9 + 13$
$‐17 + 28$	$‐9 + 2$

10s

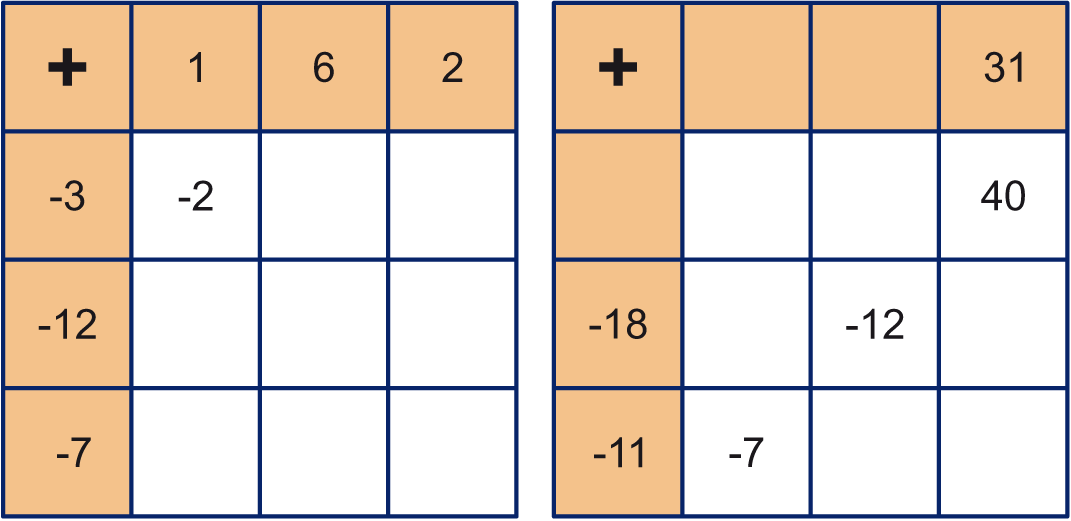
In de twee opteltabellen moeten de drie getallen aan de bovenkant opgeteld worden bij de drie getallen aan de linker zijkant. Als voorbeeld is 1 bij $‐3$ opgeteld: uitkomst $‐2$ .

Neem de opteltabellen over en vul ze verder in.

We hebben alleen nog maar warme blokjes uit de bak gehaald of erbij gegooid. We kunnen dit ook met de koude blokjes doen.

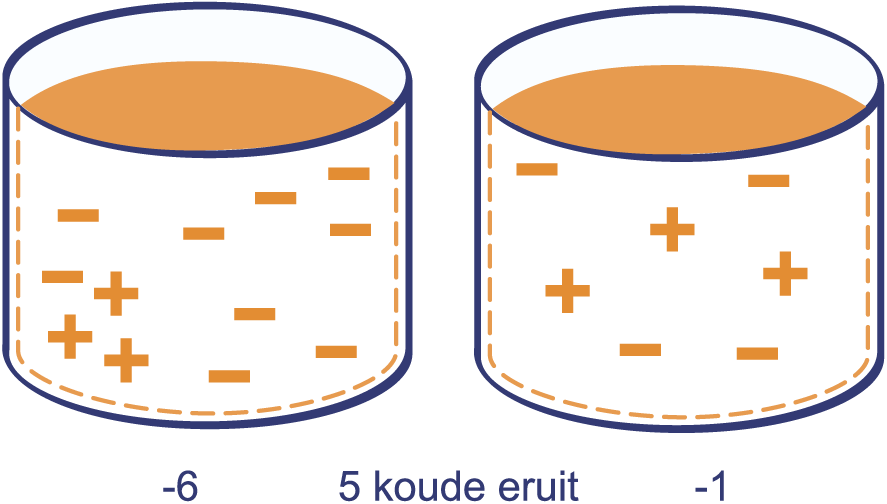
In de linker bak is de temperatuur $‐6$ graden (in deze bak zitten dus 6 koude blokjes meer dan warme). Als je 5 koude blokjes uit deze bak haalt, dan stijgt de temperatuur met 5 graden. De temperatuur wordt ${‐1}^{\circ}$ . Dus $‐6 - ‐5 = ‐1$ .

Je had de temperatuur ook met 5 graden kunnen laten stijgen door 5 warme blokjes in de bak te gooien.

Het blijkt dat $‐6 - ‐5$ hetzelfde is als $‐6 + 5$ .
Koude blokjes weghalen komt dus op hetzelfde neer als warme blokjes toevoegen.

Bereken:

$‐5 - ‐4$	$‐5 - ‐10$
$‐5 - ‐5$	$‐5 - ‐14$
$‐5 - ‐6$	$‐5 - ‐17$

11s

12s

In de twee aftrektabellen moeten de drie getallen aan de bovenkant afgetrokken worden van de drie getallen aan de linker zijkant. Als voorbeeld is $‐1$ van 2 afgetrokken: uitkomst 3.
Neem de aftrektabellen over en vul ze verder in.

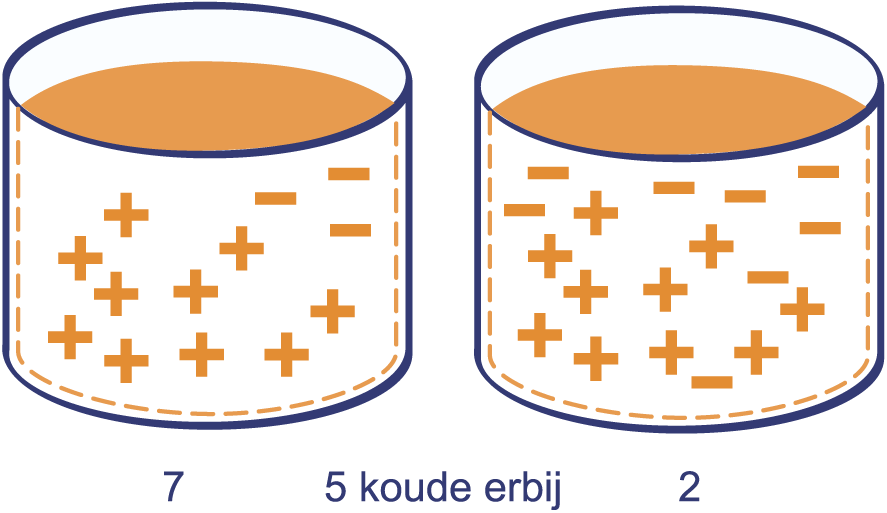
In de linker bak is de temperatuur 7 graden. Als je 5 koude blokjes in deze bak gooit, dan daalt de temperatuur met 5 graden. De temperatuur wordt 2 graden. Dus $7 + ‐5 = 2$ .
Je had de temperatuur ook met 5 graden kunnen laten dalen door 5 warme blokjes uit de bak te halen.
Het blijkt dat $7 + ‐5$ hetzelfde is als $7 - 5$ .
Koude blokjes toevoegen komt dus op hetzelfde neer als warme blokjes weghalen.

Bereken:

$12 + ‐7$	$‐7 + ‐11$
$23 + ‐11$	$‐13 + ‐27$
$17 + ‐19$	$‐35 + ‐49$

13s

14s

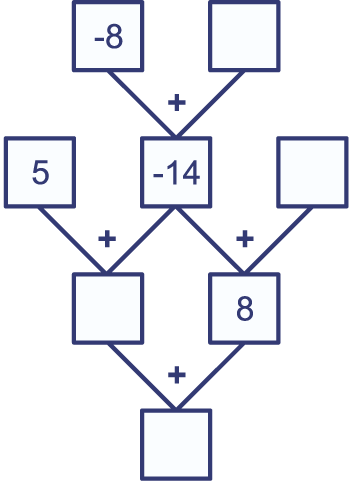
Neem het schema over en vul de open plaatsen in.

In de opgaven 9 tot en met 12 heb je gezien dat:

warme blokjes weghalen op hetzelfde neerkomt als koude blokjes toevoegen;
warme blokjes toevoegen op hetzelfde neerkomt als koude blokjes weghalen.

Maak de volgende berekeningen. Maak eerst van de aftrekking een optelling. Bij de eerste twee opgaven is al een begin gemaakt.
$3 - ‐8 = 3 + 8 =$
$‐2 - ‐5 = ‐2 + 5 =$
$0 - ‐8$
$5 - 13$
$‐6 - 3$

Bedenk drie opgaven die als uitkomst $‐7$ hebben. In de opgaven moeten steeds twee gehele getallen bij elkaar worden opgeteld.

Bedenk drie opgaven die als uitkomst $‐7$ hebben. In de opgaven moeten steeds gehele getallen van elkaar worden afgetrokken.

Bereken:
$‐5 + 3 + ‐2$
$4 + ‐8 + 3$
$‐2 + ‐7 + ‐1$
$‐8 + 12 + ‐4$

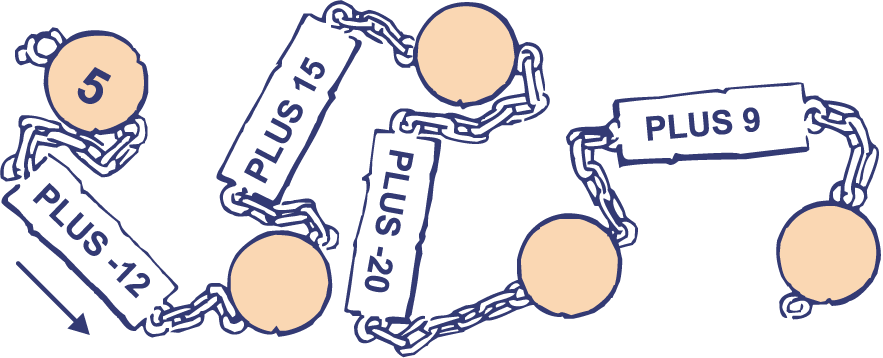
Op je werkblad staat ook de ketting van machientjes.

Vul in de ketting de juiste getallen in.

Neem de tabel over en vul hem verder in.

als je begint met	5	6	$‐6$	0
eindig je met

Het getal waarmee je eindigt is kleiner dan het getal waar je mee begint.

Welk getal moet je bij je begingetal optellen om het eindgetal te krijgen?

15s

19s

Pacman lust graag getallen. Hij start linksonder en eindigt altijd rechtsboven bij $‐5$ . Hij mag daarbij alleen maar naar rechts of naar boven.
Als Pacman helemaal naar rechts gaat en dan naar boven, is de som van de getallen die hij gegeten heeft 0, want $2 + ‐3 + 7 + 1 + ‐2 + ‐5 = 0$ .

Op hoeveel manieren kan Pacman lopen?

Hoe moet Pacman lopen om $‐1$ te eten? En $‐5$ ?

Wat is de minimale som? En de maximale?

16s

20s

In hoofdstuk 1 heb je de getallen 1 tot en met 9 op de rug van een schildpad geplaatst, zodanig dat er een tovervierkant ontstond. In elke rij, kolom en diagonaal was de som van de getallen steeds gelijk.
In plaats van alleen positieve getallen te gebruiken, kunnen we natuurlijk ook tovervierkanten maken met daarin positieve en/of negatieve getallen.
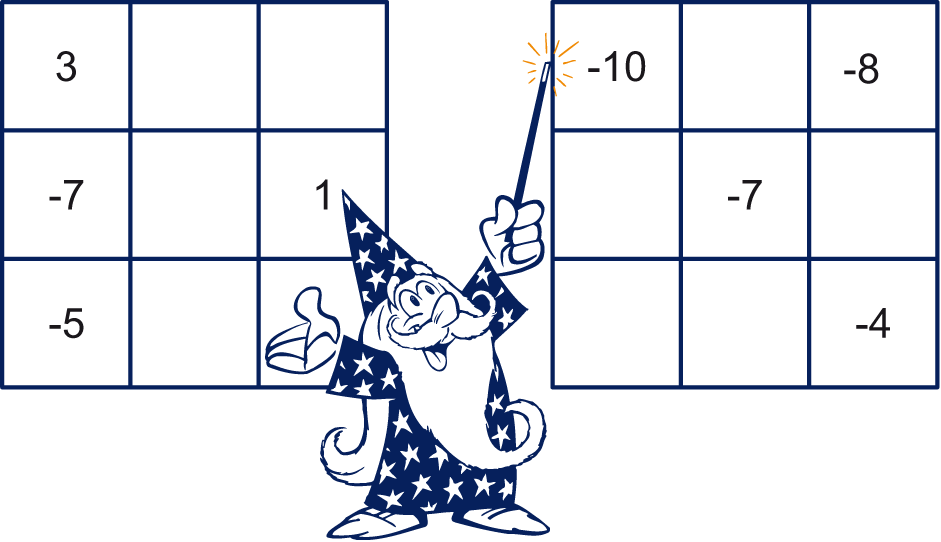
Neem de vierkanten over en vul ze verder in zodanig dat er twee tovervierkanten ontstaan.

Opmerking:

Om het optellen en aftrekken met negatieve getallen nog extra te oefenen, tot je het snel en foutloos doet, kun je meerdere keren de volgende mini-loco maken.
Optellen en aftrekken met negatieve getallen .