Veelvouden

De even getallen.

Hij vergeet veelvoud 0 mee te tellen.

$300 + 4 \times 4 = 316$ ; $300 + 9 \times 4 = 336$

$400 = 300 + 25 \times 4$ , dus het 26^ste veelvoud.

26 veelvouden, zie d.

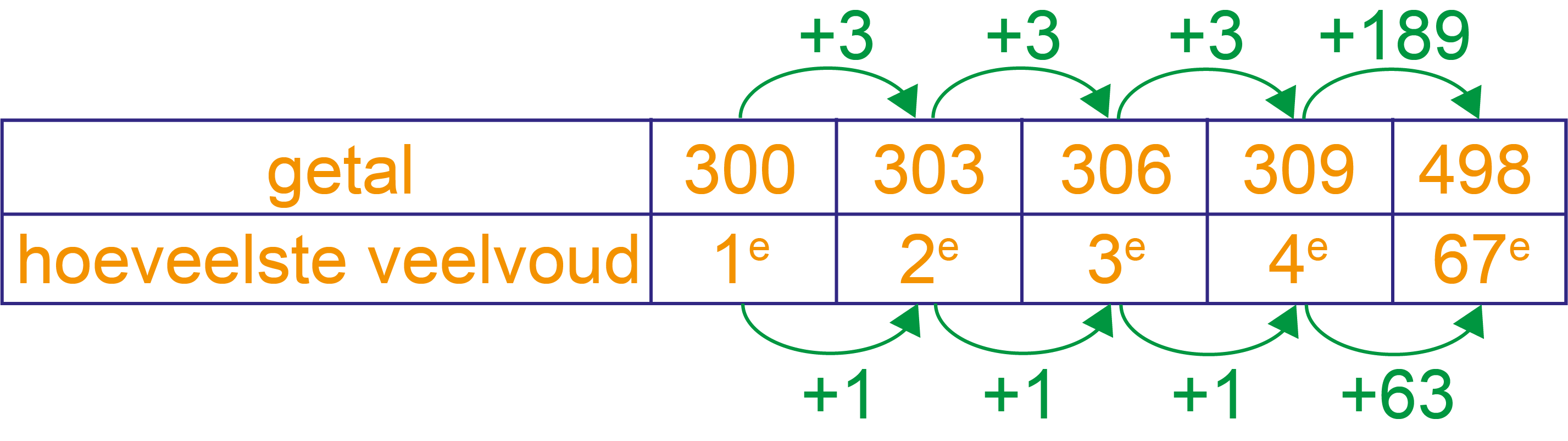
$300 = 300 + 0 \times 3$ ; $303 = 300 + 1 \times 3$ enzovoort en $498 = 300 + 66 \times 3$ , dus het zijn er even veel als getallen van 0 tot en met 66. Het zijn er dus 67.
Of zie tabel hieronder.

Nee; ja

Dat zijn de even getallen.

Nee; ja

Die eindigen op een 0 of op een 5.

0, 10, 20, 30, 40, 50, 60, 70, 80, 90

Van het getal 10.

Van het getal $3 \times 4 = 12$ .

Van het getal $5 \times 7 = 35$ .

20 ; 60 ; 240

$KGV (10,30) = 30$ ; $KGV (7,21) = 21$ ; $KGV (12,360) = 360$

$KGV (2,3) = 6$ ; $KGV (10,3) = 30$ ; $KGV (25,36) = 900$

$KGV (6,12) =$ 12, want
veelvouden van 6: 6, 12, 18, 24, …
veelvouden van 12: 12, 24, 36, …
$KGV (10,15) =$ 30, want
veelvouden van 10: 10, 20, 30, 40, …
veelvouden van 15: 15, 30, 45, …
$KGV (32,25) =$ 800, want
veelvouden van 32: 32, 64, 96, …, 736, 768, 800
veelvouden van 25: 25, 75, 100, …, 750, 775, 800

Delers

1; 12; 2; 6; 3; 4

1; 30; 2; 15; 3; 10; 5; 6

1; 2; 3; 6

Van het getal 6.

$GGD (24,42) =$ 6, want
delers van 24: 1, 2, 3, 4, 6, 8, 12, 24
delers van 42: 1, 2, 3, 6, 7, 14, 21, 42

$GGD (36,72) =$ 36
36 is een deler van 36 (de grootste deler) en van 72.

$GGD (25,32) =$ 1, want
delers van 25: 1, 5, 25
delers van 32: 1, 2, 4, 8, 16, 32

Als de $GGD$ van de twee 1 is.

Priemgetallen

2; 3; 5; 7, maar ook bijvoorbeeld 37.

Dan zouden alle getallen in de eerste "ronde" al weggestreept zijn.

Nee, want je kunt het delen door 3.

101