12.1 De oppervlakte onder een grafiek >

Hoofdstukken > De integraal

In deze paragraaf leer je de oppervlakte onder een grafiek exact te berekenen. We gaan ook in op de betekenis van zo'n oppervlakte.

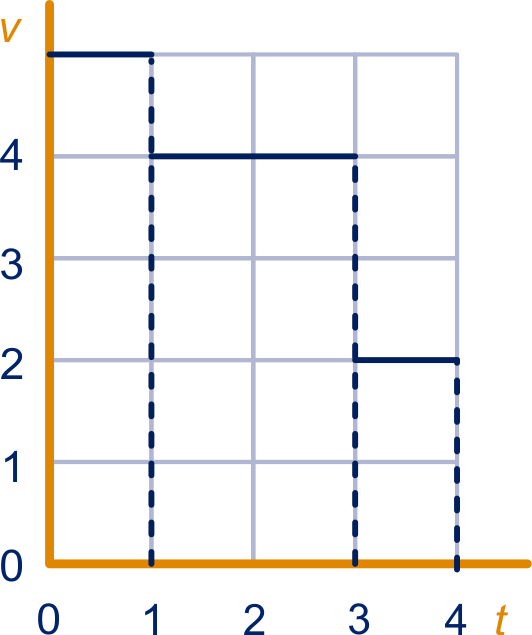
Jaap loopt $4$ uur, het eerste uur met een snelheid van $5$ km/u, de twee uren daarna met een snelheid van $4$ km/u en het laatste uur met een snelheid van $2$ km/u.
In de figuur is $v$ de snelheid in km/u en $t$ de looptijd in uur.

Hoe lang is het traject?

De wandelaar heeft na $t$ uur lopen $w (t)$ km afgelegd.

Teken de grafiek van $w$ als functie van $t$ .

Geef een formule voor $w (t)$ :

$w (t) = \dots$	als $0 \leq t \leq 1$ ,
$w (t) = \dots$	als $1 \leq t \leq 3$ ,
$w (t) =$ $7 + 2 t$	als $3 \leq t \leq 4$ .

Geef op elk tijdsinterval uit b de groeisnelheid van $w$ .

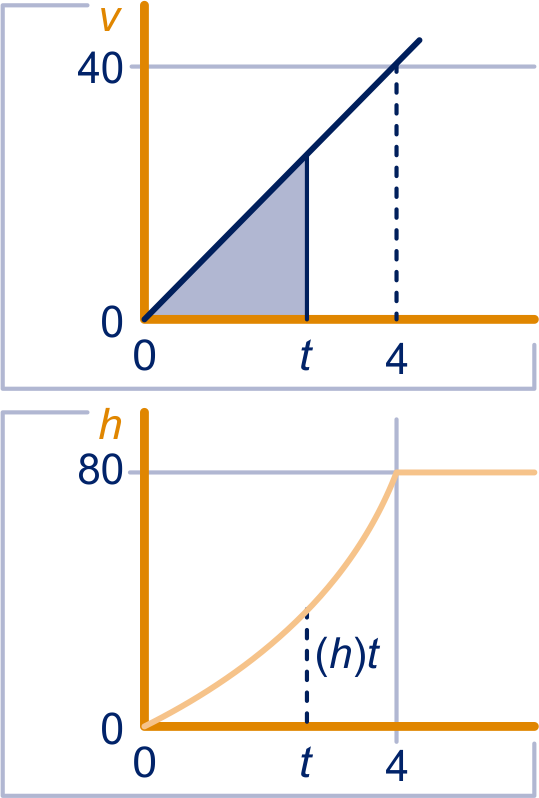
Een voorwerp valt van een toren van $80$ meter hoog. Na $t$ seconden vallen is het voorwerp $h (t) = 5 t^{2}$ meter gevallen en is zijn snelheid $v (t) = 10 t$ m/s. Hiernaast zijn de grafieken getekend van $h$ en $v$ , beide als functie van $t$ .

Druk de oppervlakte van de gekleurde driehoek in $t$ uit.

Wat is het verband tussen $h (t)$ en de oppervlakte?

Een auto rijdt in vier uur een bepaald traject.

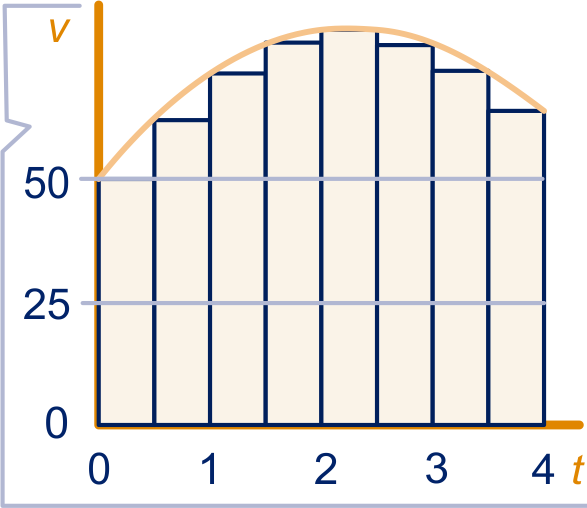
figuur 1

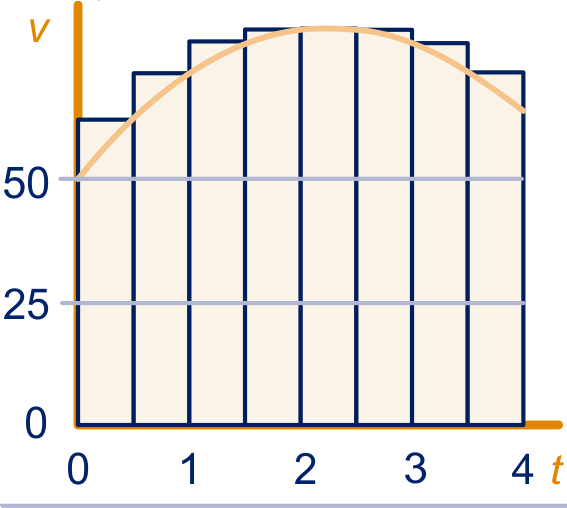
figuur 2

In figuur 1 en 2 is $v$ de snelheid in km/u en $t$ de tijd in uren. De totale lengte van het traject is $L$ km. In figuur 1 zijn, passend onder de grafiek, rechthoeken getekend. De som van de oppervlakten van die rechthoeken is $266$ km. Dat is een te lage schatting van $L$ : een zogenaamde onderschatting van $L$ .

Leg dat uit.

In figuur 2 zijn, passend boven de grafiek, rechthoeken getekend. De som van de oppervlakten van die rechthoeken in het tweede plaatje is $302$ . Dat is een bovenschatting van $L$ .

Hoe groot schat jij $L$ op grond van de onder- en bovenschatting?

Hoe zou je nog een betere schatting kunnen geven?

Hoe nauwkeurig een schatting is.
We nemen de functie $f : x \to x^{2}$ op het interval $[0,1]$ . We verdelen het interval in tien gelijke delen. De verdeelpunten zijn $0$ , $\frac{1}{10}$ , $\frac{2}{10}$ ,..., $\frac{9}{10}$ , $1$ . We maken een onderschatting en een bovenschatting van de oppervlakte onder de grafiek van $f$ met rechthoeken bij deze verdeling. In de figuur hieronder zie je links de rechthoek van de onderschatting op het interval met eindpunten $\frac{6}{10}$ en $\frac{7}{10}$ ; rechts de rechthoek van de bovenschatting.

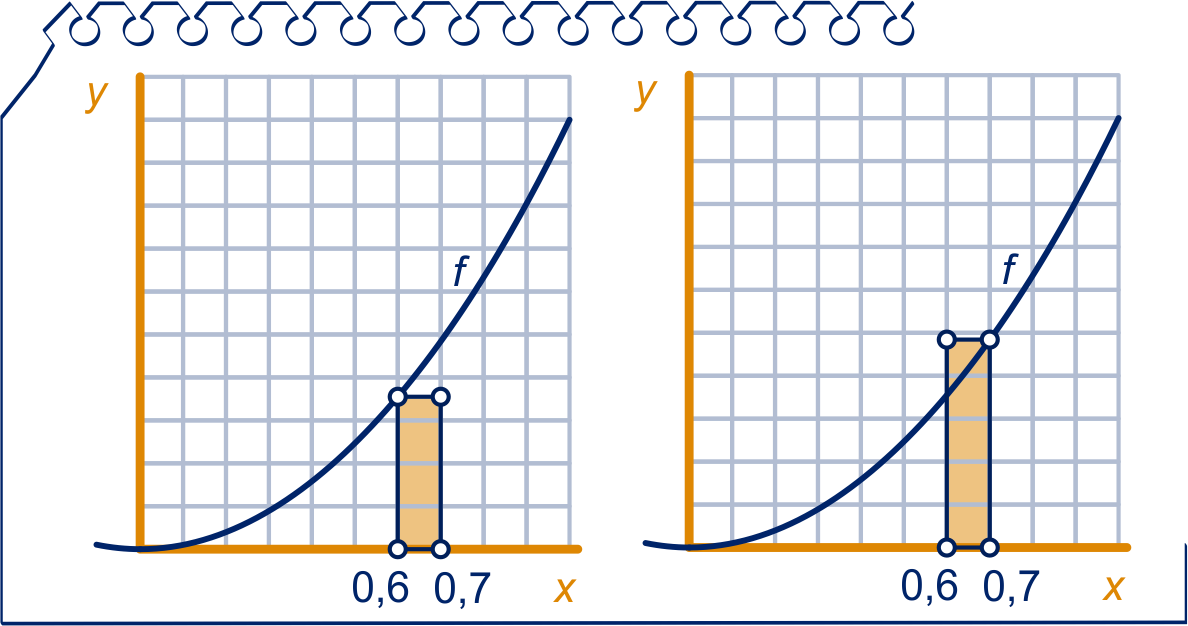
Bereken de oppervlakte van beide staven.

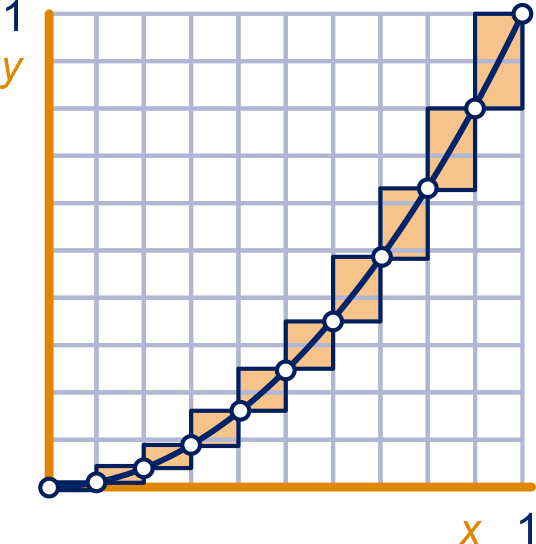
De onderschatting van de oppervlakte onder de grafiek van $f$ op het interval $[0,1]$ is:
$\frac{1}{10} \cdot 0 + \frac{1}{10} \cdot {(\frac{1}{10})}^{2} + \frac{1}{10} \cdot {(\frac{2}{10})}^{2} + ... + \frac{1}{10} \cdot {(\frac{9}{10})}^{2} =$ $0,285$
en van de bovenschatting:
$\frac{1}{10} \cdot {(\frac{1}{10})}^{2} + \frac{1}{10} \cdot {(\frac{2}{10})}^{2} + ... + \frac{1}{10} \cdot {(\frac{9}{10})}^{2} + \frac{1}{10} \cdot 1^{2} =$ $0,385$ .
Het verschil is $0,1$ . Dat het verschil $0,1$ is, kun je ook met de figuur hiernaast zien.

Leg dat uit.

Wat is het verschil tussen de onder- en bovenschatting als de rechthoeken breedte $0,01$ hebben?

Jaap benadert de oppervlakte onder de grafiek van $f : x \to x^{2}$ op $[0,2]$ met een onderschatting met twintig rechthoeken met breedte $0,1$ en ook met een bovenschatting.

Wat is het verschil tussen de onder- en bovenschatting?

G.F.B. Riemann
1826-1866

Om de oppervlakte onder de grafiek van een positieve functie te benaderen, kun je een onder-/overschatting met rechthoeken maken zoals in opgave 3.
Zo'n onder-/overschatting wordt beter naarmate je met smallere rechthoeken werkt, zie opgave 4. Zodoende krijg je een steeds nauwkeuriger schatting van de oppervlakte onder de grafiek van $f$ . Bij de functies die wij behandelen kun je het verschil tussen ondersom en bovensom zo klein maken als je maar wilt. De oppervlakte onder de grafiek van $f$ is de grenswaarde of limiet van de ondersom (en van de bovensom) bij een steeds fijnere verdeling. Om de oppervlakte onder de grafiek te bepalen is het niet noodzakelijk een regelmatige verdeling te nemen. Het doet er ook niet toe of je de grenswaarde van de boven- of ondersom neemt. We spreken - dit alles in het midden latend - over (de grenswaarde van) een Riemannsom. De methode om de oppervlakte onder de grafiek met een steeds fijnere verdeling van rechthoeken te benaderen is afkomstig van de Duitse wiskundige Bernhard Riemann.
Zo'n som wordt genoteerd met $\sum f (x) Δ x$ . Het sigma-teken $\sum$ geeft aan dat de som wordt genomen, de rechthoeken hebben oppervlakte $f (x) Δ x$ .
Conclusie
$L$ (opgave 3) is de oppervlakte onder de grafiek van $v$ .

Het bepalen van de oppervlakte onder de grafiek van een functie heet integreren, dat wil zeggen: het totaal nemen.

In de opgaven 1, 2 en 3 hebben we gezien dat de oppervlakte onder de snelheidsgrafiek van een functie $v$ op een bepaald tijdsinterval gelijk is aan de afgelegde weg $s$ op dat tijdsinterval.
In het hoofdstuk Inleiding differentiëren van 4vb heb je gezien dat de hellingfunctie van de afgelegde-weg-grafiek $s$ de snelheidsgrafiek oplevert.
Differentiëren en integreren hebben omgekeerde werking.

Archimedes
287-212 v.Chr.

De oppervlakte van gebieden met kromme grenzen is in het algemeen niet zo gemakkelijk te bepalen. Het bekendste voorbeeld is de cirkel. Daarvan was de oppervlakte al in de Griekse oudheid bekend. Archimedes wist ook de exacte oppervlakte onder de grafiek van $y = x^{2}$ op op het interval $[0,1]$ exact te berekenen.
Hoe Archimedes de oppervlakte van een cirkel benaderde kun je vinden op de website van Dick Klingens.
In de volgende opgave bekijken we hoe hij de oppervlakte van een paraboolsegment bepaalde.
In de 16de eeuw, met de uitvinding van de differentiaal- en integraalrekening, is het berekenen van de oppervlakte van "kromme" gebieden sterk vereenvoudigd.

Gegeven is de functie $f : x \to x^{2}$ op het interval $[0,1]$ . Links is de grafiek getekend in een rooster met hokjes van $0,05$ bij $0,05$ . Hiermee kun je een schatting maken van de oppervlakte onder de grafiek. In opgave 4 hebben we gezien dat die oppervlakte tussen $0,285$ en $0,385$ ligt.

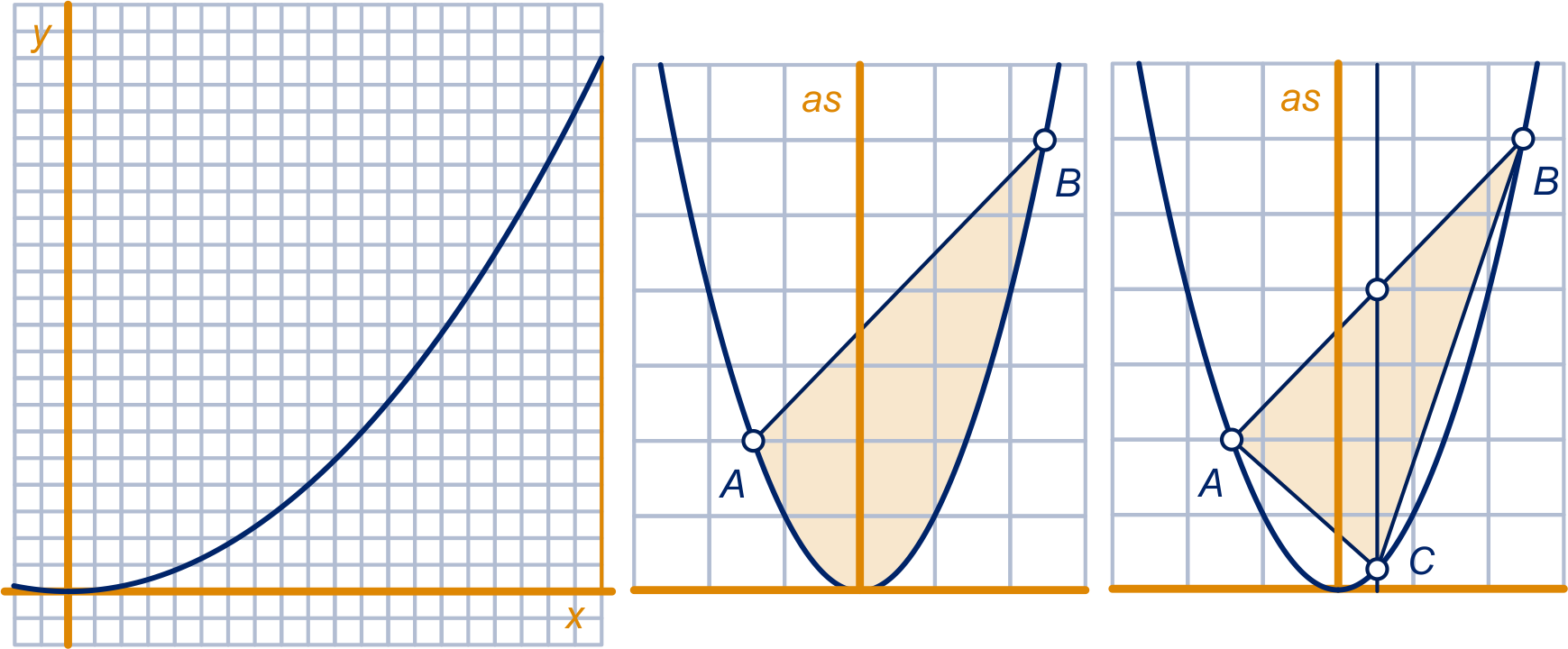
Maak een schatting van de oppervlakte onder de grafiek.

In het midden is een parabool $p$ getekend met daarop de punten $A$ en $B$ . Het vlakdeel begrensd door $p$ en lijnstuk $A B$ noemen we een paraboolsegment. Volgens Archimedes is de oppervlakte van het segment $1 \frac{1}{3}$ maal de oppervlakte van driehoek $A B C$ , waarbij $C$ het snijpunt is van $p$ met de lijn door het midden van lijnstuk $A B$ evenwijdig aan de as van de parabool, zie de tekening rechts.
Zie B.L. van der Waerden: "Ontwakende wetenschap", blz 238, P. Noordhoff nv, Groningen.

Bereken de oppervlakte onder de parabool op het interval $[0,1]$ volgens de werkwijze van Archimedes.

We bekijken de oppervlakte onder de grafiek van de functie $f : x \to x^{2}$ op het interval $[0, t]$ , met $t > 0$ . We noemen die oppervlakte $O (t)$ , zie de figuur hieronder links. We laten zien dat $O$ een primitieve van $f$ is.

Laat met de methode van Archimedes (zie opgave 5) zien dat $O (t) = \frac{1}{3} t^{3}$ .

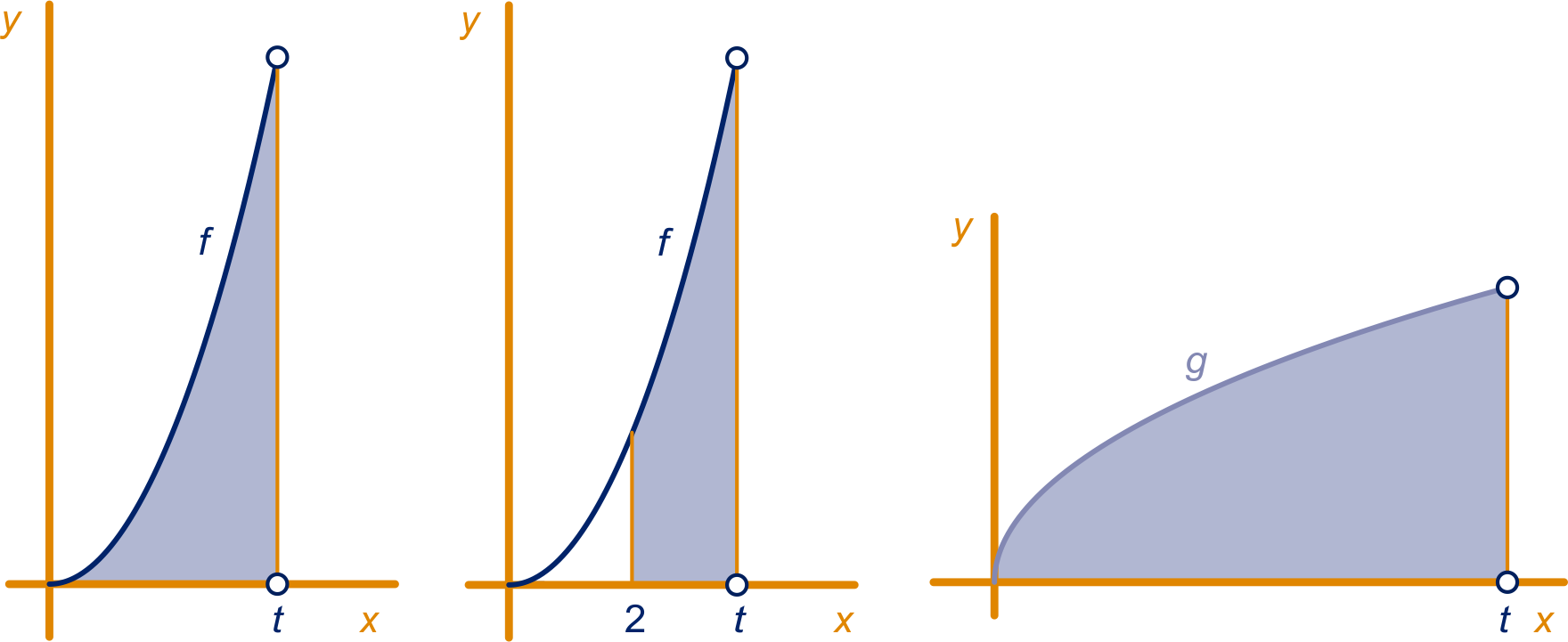
Geef $O^{'} (t)$ .

$P (t)$ is de oppervlakte onder de grafiek van de functie $f$ op het interval $[2, t]$ met $t > 2$ , zie de figuur hierboven midden.
Je kunt met de methode van Archimedes een formule voor $P (t)$ geven. Maar eenvoudiger is het om $O (t) = \frac{1}{3} t^{3}$ te gebruiken.

Laat zien hoe en geef ook $P^{'} (t)$ .

De oppervlakte onder de grafiek van de functie $g : x \to \sqrt{x}$ op het interval $[0, t]$ met $t > 0$ , noemen we $G (t)$ , zie de figuur hierboven rechts.

Geef een exacte formule voor $G (t)$ met behulp van de formule voor $O (t)$ die je gevonden hebt.

Wat is $G^{'} (t)$ ?

Een functie $F$ heet primitieve functie van de functie $f$ als $F^{'} (x) = f (x)$ voor alle $x$ .

In opgave 6 heb je gezien dat de functie
$f : x \to x^{2}$ als primitieve de functie $O$ met $O (x) = \frac{1}{3} x^{3}$ heeft,
$g : x \to \sqrt{x}$ als primitieve de functie $G$ met $G (x) = \frac{2}{3} x \sqrt{x}$ heeft. Niet alleen $O$ (onderdeel 6a is een primitieve van $f$ , maar ook $P : x \to \frac{1}{3} x^{3} - 2 \frac{2}{3}$ onderdeel 6c.)

Stelling 1
Gegeven is een functie $f$ op het interval $[a, b]$ .
Als $F$ een primitieve van $f$ is, dan is de functie $x \to F (x) + c$ ook een primitieve van $f$ voor elke constante $c$ .
Omgekeerd: als $F_{1}$ en $F_{2}$ primitieven zijn van $f$ , dan is $F_{1} - F_{2}$ constant.

Het eerste deel van de stelling is waar. Dat het omgekeerde ook waar is, bewijzen we niet.

Opmerking:

Een voorwerp beweegt. De afgelegde weg $s (t)$ meter (kilometer,...,...) na $t$ seconden (uren,...,...) is een primitieve van de snelheid $v (t)$ in m/s (km/u,...,...).
De afgelegde weg gedurende het tijdsinterval $[a, b]$ is de oppervlakte onder grafiek van $v$ .

Een automobilist laat zijn auto uitlopen bij het naderen van de 30km-zone. Zijn snelheid $v (t)$ na $t$ seconden is:
$v (t) = 9 + \frac{20}{t + 4}$ m/s.
De grafiek van $v$ op het tijdsinterval $[0,30]$ staat hieronder.

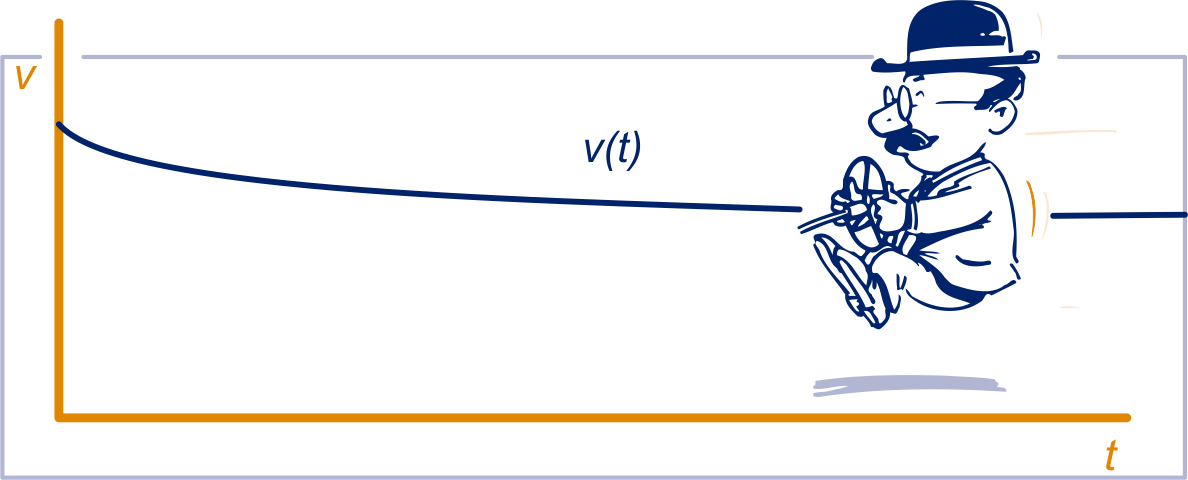
Bereken de snelheid van de auto op $t = 0$ en $t = 30$ in km/u.

De afgelegde weg na $t$ seconden $s (t)$ is primitieve functie van $v (t)$ .

Ga na dat de functie $t \to 9 t + 20 \cdot \ln (t + 4)$ een primitieve is van $v (t)$ .

Dus volgens de stelling geldt: $s (t) = 9 t + 20 \cdot \ln (t + 4) + c$ , voor een of ander constante $c$ .
Het getal $c$ kun je vinden omdat je $s (0)$ kent.

Wat is $s (0)$ ? Bereken $c$ hieruit exact.

Bereken exact hoeveel meter de auto heeft afgelegd op het tijdsinterval $[0,30]$ . Geef ook een benadering in twee decimalen.

Wat is de gemiddelde snelheid van de auto (in km/u) op het tijdsinterval $[0,30]$ . Geef je antwoord in één decimaal.

Opmerking:

Als de snelheid van een auto niet constant is, kun je de gemiddelde snelheid van de auto op een bepaald tijdsinterval uitrekenen door de oppervlakte onder de grafiek op dat interval te delen door de lengte van het interval.

De figuur links gaat over een race tussen twee auto's, $v$ is de snelheid en $t$ de tijd. Op $t = 0$ is de start.

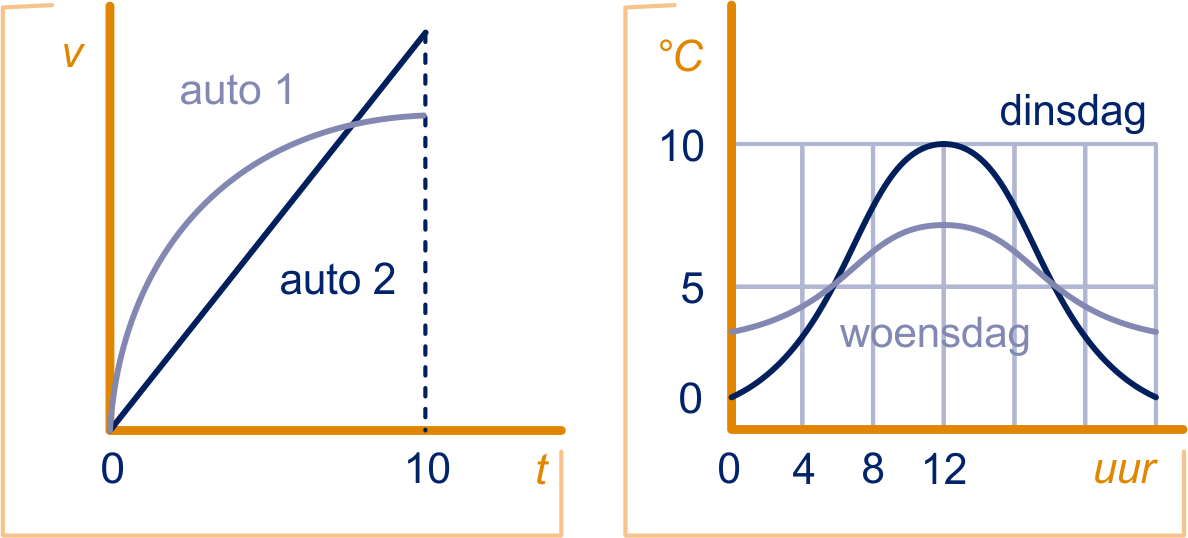
Welke auto ligt voor op $t = 10$ ? Hoe zie je dat aan de grafieken?

In de figuur rechts zie je grafieken van het temperatuurverloop op twee dagen in Boxmeer, een dinsdag en een woensdag.

Op welke dag was de gemiddelde temperatuur het hoogst? Waarom?

Gegeven is de functie $f : x \to \sin^{2} (x)$ . Hieronder is de grafiek getekend op het domein $[0,2 π]$ .

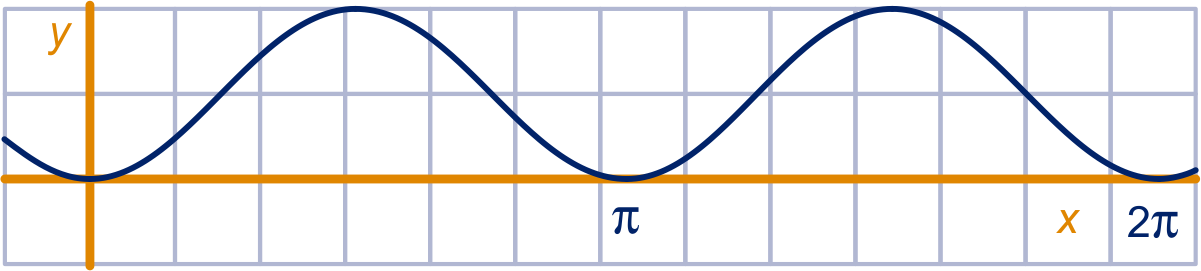
Met knippen en plakken kun je een rechthoek van het gebied onder de grafiek van $f$ maken.

Laat zien hoe dat gaat.
Wat is dus de oppervlakte exact?

Wat is de oppervlakte onder de grafiek van de functie
$g : x \to 3 \sin^{2} (x)$ op $[0,2 π]$ exact?

Wat is de oppervlakte onder de grafiek van de functie
$h : x \to \sin^{2} (\frac{1}{2} x)$ op $[0,2 π]$ exact? Licht je antwoord toe.

Er wordt een spanningsverschil $V$ over een weerstand (bijvoorbeeld een lamp) gezet. Uit de natuurkunde is bekend dat het afgegeven vermogen $W$ evenredig is met $V^{2}$ .
De wisselspanning via een stopcontact is sinusvormig met $50$ periodes per seconde ( $50$ hz). Het spanningsverschil in Europa is $230$ volt. Dat wil zeggen dat de afgegeven energie over een bepaald tijdsinterval hetzelfde is als dat van een gelijkspanning (constante spanning) van $230$ volt. Neem aan dat de wisselspanning amplitude $V$ heeft.
De afgegeven energie op een bepaald tijdsinterval is de oppervlakte onder het vermogen $W$ op dat interval.
Als je de afgegeven energie van de wissel- en gelijkspanning over één periode met elkaar vergelijkt vind je: $\frac{1}{2} \cdot V^{2} = 230^{2}$ , dus $V = 230 \sqrt{2}$ .

In de voorgaande twee opgaven hebben we gezien dat de oppervlakte onder de grafiek van een functie een belangrijke rol speelt.
We eindigen deze paragraaf met een mooie tekst van Piet Grijs (pseudoniem van Hugo Brandt-Corstius.)