Kanker is een van de belangrijkste doodsoorzaken. Een kwaadaardig gezwel ontstaat als een normale lichaamscel verandert in een tumorcel, die gaat zich dan op eigen houtje delen. Bij de eerste deling ontstaan twee tumorcellen, bij de volgende deling vier, daarop acht, dan zestien, enzovoort.

Hoeveel tumorcellen zijn er na de vijfde en na de zesde deling?

Na hoeveel delingen zijn er meer dan $2000$ tumorcellen?

Zoek met je rekenmachine uit na hoeveel delingen er meer dan een miljoen tumorcellen zijn.

Zeg dat een tumorcel een inhoud heeft van $1$ miljoenste mm³.

Ga met een berekening na dat er dan na veertig delingen een (dodelijke) tumor is van meer dan $1$ dm³.

In de vorige opgave is de groeifactor per uur gelijk aan $2$ .
Dat betekent: als je op een bepaald moment een aantal bacteriën hebt, dan heb je er een uur later dubbel zoveel.
Het maakt dan niet uit hoeveel je er in het begin hebt: als je begint met $100$ , dan heb je er een uur later $200$ . Maar als je begint met $1000$ , dan heb je een uur later $2000$ stuks.

Dit is een belangrijke kenmerk van exponentiële groei: per tijdseenheid groeit de hoeveelheid met een vaste factor. Deze factor noemen we de groeifactor.

Op een gegeven moment (tijdstip $0$ ) zijn er in een kweek $1000$ bacteriën. De bacteriën delen zich gemiddeld elk uur.

Hoeveel bacteriën zijn er na $3$ uur? En na $12$ uur?
En na $t$ uur?

Maar hoeveel bacteriën zijn er na een half uur?
Ook per half uur is er een constante groeifactor. Deze groeifactor noemen we $g$ .

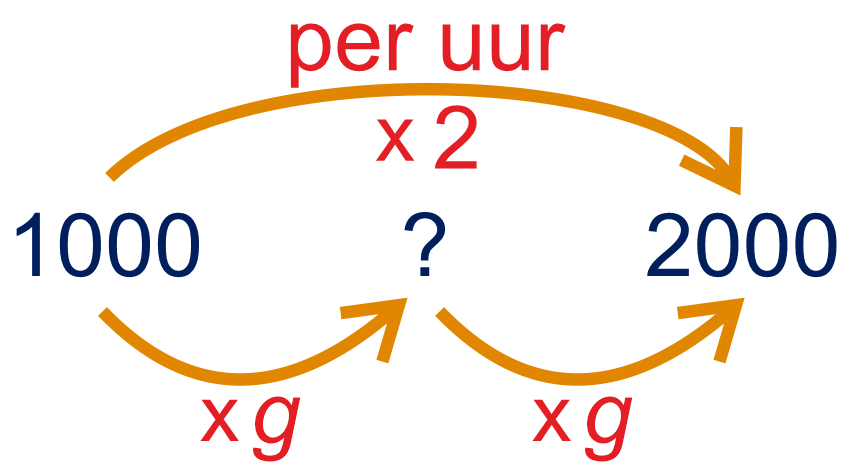
Dan geldt dus $1000 \cdot g^{2} = 2000$ , ofwel $g^{2} = 2$ .

Wat is de exacte groeifactor $g$ per half uur?
Hoeveel bacteriën zijn er dus na een half uur?
Hoeveel bacteriën zijn er na $5$ halve uren (dus na $2,5$ uur)?
Geef een formule voor het aantal bacteriën $B$ na $t$ halve uren.

Ook per $20$ minuten is er een constante groeifactor. Deze groeifactor noemen we weer $g$ .
Dan geldt dus $1000 \cdot g^{3} = 2000$ , ofwel $g^{3} = 2$ .

Wat is de exacte groeifactor $g$ per $20$ minuten?
Hoeveel bacteriën zijn er dus na $20$ minuten?
Hoeveel bacteriën zijn er na $100$ minuten (dus na vijf keer $20$ minuten)?
Geef een formule voor het aantal bacteriën $B$ na $t$ keer $20$ minuten.

Ook per kwartier is er een constante groeifactor. Deze groeifactor noemen we weer $g$ .

Wat is de exacte groeifactor $g$ per kwartier?
Hoeveel bacteriën zijn er dus na een kwartier?
Hoeveel bacteriën zijn er na $5$ kwartier?
Geef een formule voor het aantal bacteriën $B$ na $t$ kwartieren.

In opgave 14 groeit het aantal bacteriën volgens de formule $B = 1000 \cdot 2^{t}$ , met $t$ in uren.
Als je het aantal na een half uur wilt weten, bleek de groeifactor $\sqrt{2}$ te zijn: $B = 1000 \cdot \sqrt{2}$ .
Maar je kunt het aantal na een half uur ook vinden door in de formule $t = \frac{1}{2}$ in te vullen: $B = 1000 \cdot 2^{\frac{1}{2}}$ .
Blijkbaar geldt: $2^{\frac{1}{2}} = \sqrt{2}$ .
Evenzo geldt (per $20$ minuten): $2^{\frac{1}{3}} = \sqrt[3]{2}$ .
En (per kwartier): $2^{\frac{1}{4}} = \sqrt[4]{2}$ .

Algemeen: $2^{\frac{1}{n}} = \sqrt[n]{2}$ .
Dit geldt natuurlijk ook voor andere groeifactoren dan factor $2$ :

$g^{\frac{1}{n}} = \sqrt[n]{g}$

We willen dat de eerste rekenregel voor machten ook voor breuken geldt, dus: $\sqrt[3]{2} \cdot \sqrt[3]{2} = 2^{\frac{1}{3}} \cdot 2^{\frac{1}{3}} = 2^{\frac{2}{3}}$ enzovoort.
We maken dus de volgende afspraak.

Afspraak
Voor alle positieve getallen $a$ , $p$ en $q$ met $p$ en $q$ geheel geldt:
$a^{\frac{p}{q}} = \sqrt[q]{a^{p}} = {\sqrt[q]{a}}^{p}$ .

Hoe snel een bacteriekolonie groeit (bij ideale laboratoriumomstandigheden) hangt af van de soort. Gistermiddag schatte een bioloog het aantal bacteriën in een kolonie om 12.00 uur op $500$ en om 16.00 uur op $4500$ .

Wat is de groeifactor per $4$ uur? En per uur? Rond je laatste antwoord af op 3 decimalen.

Met hoeveel procent neemt het aantal bacteriën toe per uur?

Geef een formule voor het aantal bacteriën $t$ uur na 12.00 uur.

Onderzoek met je grafische rekenmachine op welk tijdstip de grens van een miljoen bacteriën wordt gepasseerd. Rond je antwoord af op een geheel aantal minuten.

Jaren geleden, in het tijdperk van de gulden waren er tijden van hoge inflatie. Daarom werd er in die tijd ook een hoge rente op een spaarrekening gegeven.
We volgen de groei van het kapitaal op een spaarrekening waarop jaarlijks aan het eind van het jaar $10$ % rente wordt bijgeschreven.
Het beginkapitaal op 1 januari is $1000$ gulden.
Het kapitaal na $t$ jaren sparen is $K (t)$ gulden.

Vul de tabel in.

$t$	$0$	$1$	$2$	$3$	$4$
$K (t)$

Hoeveel keer zo groot wordt het kapitaal in een jaar, ofwel wat is de groeifactor per jaar?

Hoeveel keer zo groot wordt het kapitaal in twee jaar?
Met hoeveel procent groeit het kapitaal dus in twee jaar?

Bereken $K (10)$ , de grootte van het kapitaal na $10$ jaar.

Geef een formule voor $K (t)$ uitgedrukt in $t$ .

Bereken met de grafische rekenmachine na hoeveel jaar het kapitaal is gegroeid tot meer dan $10 000$ gulden.

Hoeveel keer zo duur wordt een product als de prijs toeneemt met: $15$ %, $1,5$ %, $247$ %, $0,24$ %?
En als de prijs afneemt met: $15$ %, $1,5$ %, $99$ %, $0,24$ %?

Met hoeveel procent neemt de prijs toe of af, als het product $3$ keer zo duur wordt? Als het $0,75$ keer zo duur wordt? Als het $1,075$ keer zo duur wordt? En als het $0,15$ keer zo duur wordt?

In een winkelstraat voeren twee concurrenten een actie. De een verhoogt zijn prijzen eerst met $10$ % en geeft vervolgens $10$ % korting. De ander geeft $10$ % korting en verhoogt dan zijn prijzen met $10$ %.

Is de eerste winkelier even duur gebleven als hij voor de actie was? En de tweede?
Wie van de twee is na de actie het duurst?

Iemand koopt een pakket aandelen. Het eerste jaar stijgen de aandelen met $20$ %, het tweede jaar met $7,3$ %, het derde jaar dalen ze met $18$ % en het vierde jaar stijgen ze weer met $4,4$ %.

Met hoeveel procent is de waarde in vier jaar gestegen?

Hoe dieper je onder water komt, des te donkerder het wordt. Hoe troebeler het water, hoe minder licht het doorlaat. In zeewater bijvoorbeeld, is de hoeveelheid licht op $1$ meter diepte ongeveer $75$ % van de hoeveelheid licht dat op het wateroppervlak valt.
De hoeveelheid licht op $2$ meter diepte is $75$ % van $75$ % van de oorspronkelijke hoeveelheid licht die op het water valt.

Hoeveel procent is dat?

$y$ is de hoeveelheid licht (in procenten van de oorspronkelijke hoeveelheid) op $x$ meter diepte.

Vul de tabel in en teken de bijbehorende grafiek.

$x$	$0$	$1$	$2$	$3$	$4$
$y$	$100$	$75$

Geef een formule voor $y$ uitgedrukt in $x$ .

Ga na dat de hoeveelheid licht op $8$ m diepte $10$ % van de oorspronkelijke hoeveelheid is.

Vanaf welke diepte is de hoeveelheid licht minder dan $1$ % van de oorspronkelijke hoeveelheid?

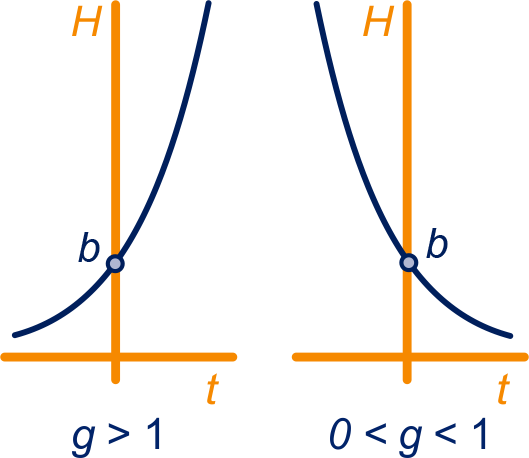
Een hoeveelheid $H$ groeit exponentieel in de tijd $t$ als $H$ gedurende elke tijdseenheid een vaste factor keer zo groot wordt: de groeifactor.
Als de beginhoeveelheid $b$ is en de groeifactor $g$ , dan moet er na elke tijdseenheid met $g$ vermenigvuldigd worden.

$t$	$0$	$1$	$2$	$3$
$H (t)$	$b$	$b \cdot g$	$b \cdot g \cdot g$	$b \cdot g \cdot g \cdot g$

Algemeen: $H (t) = b \cdot g^{t}$ .
Als $g > 1$ is $H$ stijgend. Als $0 < g < 1$ , dan is $H$ dalend.

Aan water wordt suiker toegevoegd. De suiker lost langzaam op: van de suiker die er op een bepaald moment nog over is, lost in de volgende minuut $20$ % op. Om $12.00$ u is $125$ gram suiker over. Het aantal grammen suiker dat er $t$ minuten na $12.00$ u over is noemen we $A (t)$ .

Vul de tabel in.

$t$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$
$A$	$125$

Wat is de groeifactor per minuut van de hoeveelheid suiker die over is?

Geef de formule voor $A (t)$ .

Hoeveel gram suiker was er $2$ minuten voor $12.00$ u over?

Ga met je rekenmachientje na wanneer op $1$ gram na alle suiker is opgelost.

Een bioloog doet onderzoek naar de invloed van fosfaten in het water op de groei van algen. Om de groei te kunnen bestuderen, heeft hij twee bakken met algen genomen. De ene bak bevat water met veel fosfaten, de andere fosfaatarm water. Van beide bakken bepaalt hij elke week de hoeveelheid algen. De resultaten van de bak met fosfaatrijk water staan hieronder.

Week	$0$	$1$	$2$	$3$	$4$
Hoeveelheid	$10,0$	$16,0$	$25,6$	$41,0$	$65,5$

Laat zien dat hier sprake is van exponentiële groei.

Stel een formule op voor de hoeveelheid $H (t)$ na $t$ weken.

De bioloog was in de andere bak ook begonnen met hoeveelheid $10,0$ . Na vier weken was de hoeveelheid algen gegroeid tot $22,9$ .
Ook hier verwachten we dat de groei exponentieel verloopt.
We gaan op zoek naar de groeifactor per week. Die kunnen we vinden door een aantal waarden te proberen.

Hoe groot is het oppervlak na vier weken als de hoeveelheid algen elke week $1,3$ keer zo groot wordt?
Wordt de hoeveelheid algen elke week meer of minder dan $1,3$ keer zo groot?

Kies aan de hand van je resultaat bij het vorige onderdeel een nieuwe waarde voor de groeifactor. Ga net zolang door tot je de waarde van de groeifactor op twee decimalen nauwkeurig gevonden hebt.

Opmerking:

De methode van opgave 20d om de groeifactor te vinden kost wat geduld en rekenwerk. Met de methode van opgave 14 kun je de groeifactor direct berekenen.
We zochten naar de groeifactor $g$ waarvoor geldt:
$10,0 \cdot g^{4} = 22,9$ .
Hieruit volgt: $g^{4} = 2,29$ , dus $g = {2,29}^{\frac{1}{4}} \approx 1,23$ .

Nederland verstedelijkt in een rap tempo. Vooral steden in of bij de Randstad groeien als kool. Zo ook de stad Veenendaal tussen Utrecht en Arnhem. In 1983 telde Veenendaal nog maar $42.320$ inwoners. Zes jaar later (in 1989) waren dat er al $47.358$ . In 1995 woonden er in Veenendaal $54.023$ mensen. (Gegevens op 1 januari; bron Statistisch Jaarboek)
Op 1 mei 2014 waren er $63.322$ inwoners (bron: CBS).

Neemt het aantal inwoners van Veenendaal lineair toe? Waarom wel / niet?

Hoeveel keer zo groot is het aantal inwoners van Veenendaal geworden in de periode 1983-1989? En in de periode 1989-1995?

Kun je uit je antwoord op het vorige onderdeel al afleiden of het aantal inwoners exponentieel groeit? Waarom wel/niet?

Stel dat het aantal inwoners van Veenendaal in de gehele periode 1983-1989 exponentieel groeide.

Bereken de groeifactor $g$ per jaar.
Met hoeveel procent nam het aantal inwoners gemiddeld per jaar toe in die periode?

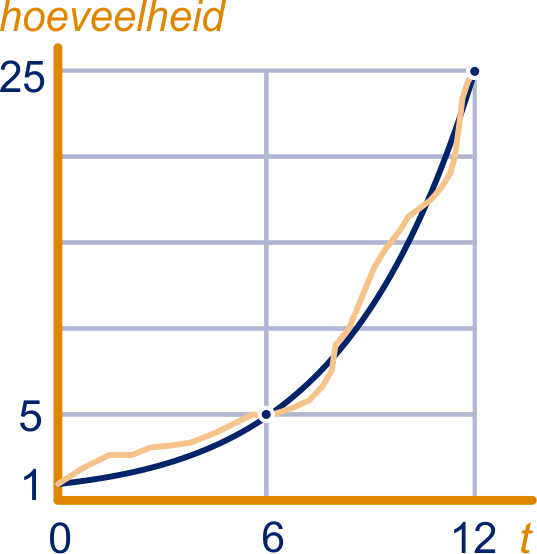
Stel dat een hoeveelheid exponentieel groeit en dat de hoeveelheid in $6$ uur tijd $5$ keer zo groot wordt. Dan geldt voor de groeifactor $g$ per uur: $g^{6} = 5$ .
Dus $g = 5^{\frac{1}{6}} = \sqrt[6]{5} (\approx 1,308)$ (de zesdemachtswortel van $5$ ).

Per uur neemt de hoeveelheid dan met $30,8$ % toe.

Ook als de werkelijke groei niet precies exponentieel is, maar tussen twee tijdstippen die $6$ uur uit elkaar liggen de hoeveelheid met factor $5$ is gegroeid (zie rode grafiek in de figuur), zeggen we dat in die periode de gemiddelde groeifactor gelijk is aan $g = 5^{\frac{1}{6}} = \sqrt[6]{5} (\approx 1,308)$ .
De hoeveelheid is dan gemiddeld per uur met $30,8$ % toegenomen.

De prijzen stijgen gemiddeld met $2$ % per jaar.

Met hoeveel procent stijgen de prijzen in $10$ jaar (in één decimaal nauwkeurig)?

Een luchtballon loopt langzaam leeg, elke dag met $3$ %.
Op een gegeven moment ( $t = 0$ ) zit er $2$ liter lucht in.

Geef een formule voor de hoeveelheid lucht $H$ in de ballon (in liter) na $t$ dagen.

Hoeveel procent lucht verdwijnt er per week uit de ballon (in één decimaal nauwkeurig).

Een hoeveelheid groeit per $70$ % per week.

Bereken in één decimaal nauwkeurig met hoeveel procent de hoeveelheid per dag groeit.

Als een hoeveelheid met $2$ % per uur afneemt, groeit die hoeveelheid exponentieel met groeifactor $0,98$ per uur.
Als een hoeveelheid met $2$ % per uur toeneemt, groeit die hoeveelheid exponentieel met groeifactor $1,02$ per uur.

Een belegger ziet zijn beleggingen in $4$ jaar groeien van $110$ miljoen tot een kwart miljard.
Neem aan dat de groei exponentieel is.

Met hoeveel procent per jaar groeit zijn belegd kapitaal?

De prijs van sommige electronica daalt spectaculair. De laatste drie jaar geeft een daling met $\frac{1}{3}$ te zien. Neem aan dat de prijs exponentieel daalt.

Bereken met hoeveel procent per jaar (in twee decimalen).