Noem de top van de piramide , de projectie van de top op het grondvlak
en een hoekpunt van het grondvlak .
, de
hoogte van de piramide is .
Er geldt: , dus
de hoogte is en de inhoud van de piramide is: .
We berekenen eerst het deel dat er afgehaald is. Dat is een piramide die gelijkvormig is met de oorspronkelijke
piramide met vergrotingsfactor , dus met inhoud
.
De afgeknotte piramide heeft dus inhoud .
De complete piramide is op halve hoogte afgeknot, want de afmetingen van het snijvlak (bovenvlak) zijn half zo groot als die van het grondvlak. De complete piramide heeft dus hoogte .
De complete piramide heeft inhoud . Het stuk dat er afgehaald is heeft inhoud . De afgeknotte piramide heeft inhoud .
Het stuk dat er afgehaald is, is een piramide gelijkvormig met de complete piramide. Noem de vergrotingsfactor van
klein naar groot , dan , dus
.
Noem de hoogte van de piramide die er afgehaald is , dan is de hoogt van de complete piramide
, dus de afgeknotte piramide heeft
hoogte , dus
en de hoogte van de complete piramide is
.
De inhoud van de complete piramide is .
De inhoud van het stuk dat er afgehaald is, heeft inhoud , dus
de afgeknotte piramide heeft inhoud .
Het stuk dat er afgehaald is, is een piramide gelijkvormig met de complete piramide. Noem de vergrotingsfactor van
klein naar groot , dan , dus
.
De hoogte van de complete piramide is .
De inhoud van de complete piramide is .
De inhoud van het stuk dat er afgehaald is, heeft inhoud , dus
de afgeknotte piramide heeft inhoud .
Het stuk dat er afgehaald is, is gelijkvormig met de complete kegel, de vergrotingsfactor van klein naar groot is .
De hoogte van de top noemen we , dan is de hoogte van de complete kegel
en van de emmer dus
, dus de hoogte van de complete kegel is:
cm.
De inhoud van de complete kegel is: dm3. De inhoud van de top is dm3, dus de inhoud van de emmer is: dm3, dus ongeveer dl.
Ze hebben alle dezelfde inhoud. De piramide aan de voorkant bijvoorbeeld heeft een grondvlak met oppervlakte en hoogte , dus inhoud .
De halve cirkel van de uitslag wordt de grondcirkel van de kegel, dus de omtrek van de grondcirkel van de kegel is . De straal van de grondcirkel is dus .
Noem de top van de kegel en het middelpunt van de grondcirkel .
Neem een punt op de grondcirkel . Dan is de schuine zijde
van driehoek gelijk aan
en de rechthoekszijde
.
Dus driehoek is een
---graden driehoek, dus de tophoek is
en de hoogte van de kegel is
.
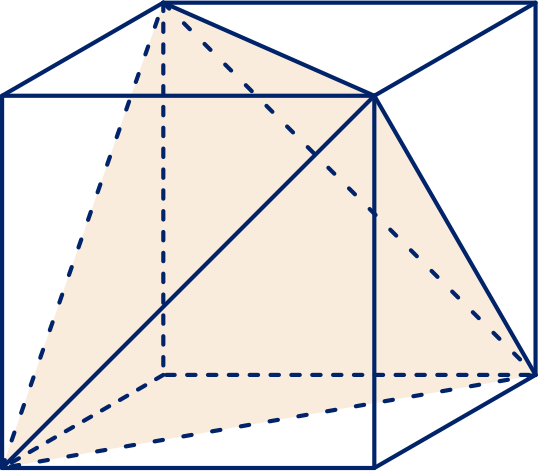
Het grondvlak van zo'n piramide is een gelijkbenige rechthoekige driehoek waarvan de rechthoekszijden
zijn en de hoogte .
De inhoud is dus .
,
,
Het huis bestaat uit een blok van bij
bij
waaruit vier piramides zijn weggehaald met een grondvlak van bij
en hoogte
.
De inhoud is dus m3.
Op hoogte m: rood, op hoogte m blauw en op hoogte m groen.

