Een soeppan is $30$ cm breed en $20$ cm hoog.

Hoeveel liter (dm³) is de inhoud?

Voor de centrale verwarming worden wel stalen buizen gebruikt met een buitendiameter van $24$ mm en een wanddikte van $2$ mm.

Bereken hoeveel zo'n buis van $1$ meter lengte weegt.
( $1$ dm³ staal weegt $7,8$ kg.)

Een moderne brandkast is dubbelwandig: tussen de buiten- en binnenwand zit isolatiemateriaal dat bestand is tegen zeer hoge temperaturen (tot $1000 °$ C).

Waarvoor dient dit materiaal?

Van een brandkast zijn de buitenmaten $102$ , $62$ en $62$ cm en de binnenmaten $88$ , $48$ en $48$ cm.
Het plaatstaal is $1$ cm dik.

Bereken hoeveel dm³ isolatiemateriaal tussen de wanden zit.

De zijkanten van een tent zijn rechthoeken, $17$ dm hoog en $20$ dm lang. Voor (en achter) is de tent $16$ dm breed.

Bereken de inhoud van de tent.

Neem van het prisma hieronder links de rechthoek van $8$ bij $3$ als grondvlak; de bijbehorende hoogte is $2$ . Door het prisma via de hoogtelijn (zie plaatje) door te zagen, krijg je twee halve balken.

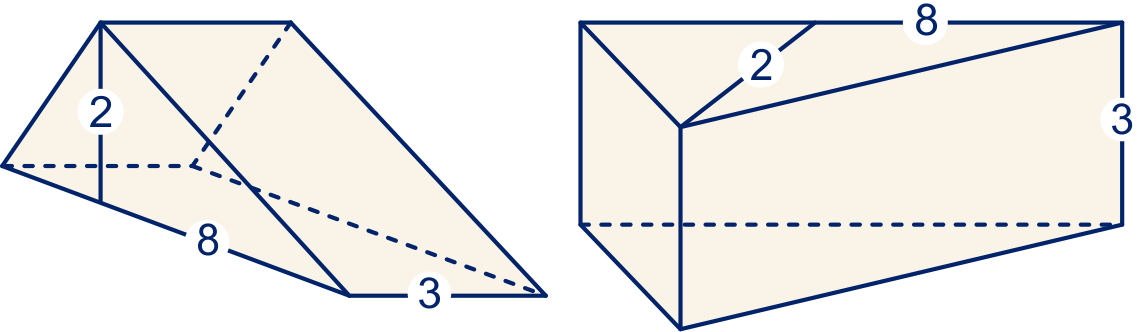
Bereken de inhoud.

Neem in de figuur rechts de driehoek als grondvlak; de bijbehorende hoogte is $3$ .

Bereken de inhoud.

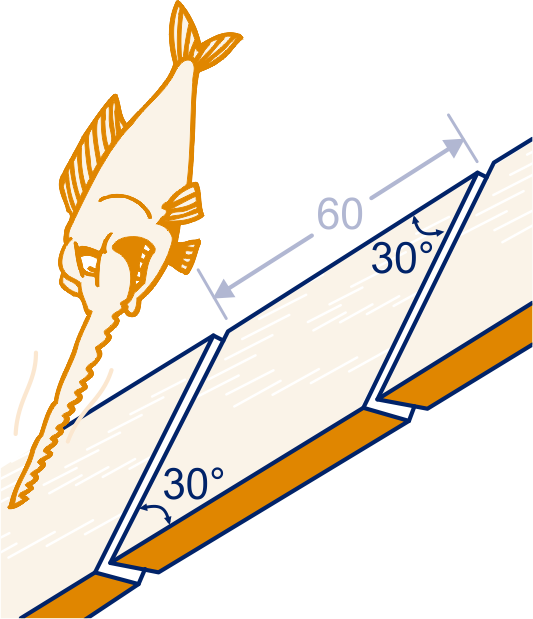
Uit een plank van $5$ cm dikte heeft iemand een stuk gezaagd met zijden van $60$ en $50$ cm. De zaagsneden maken hoeken van $30 °$ met de plank.

Bereken de inhoud van het stuk.

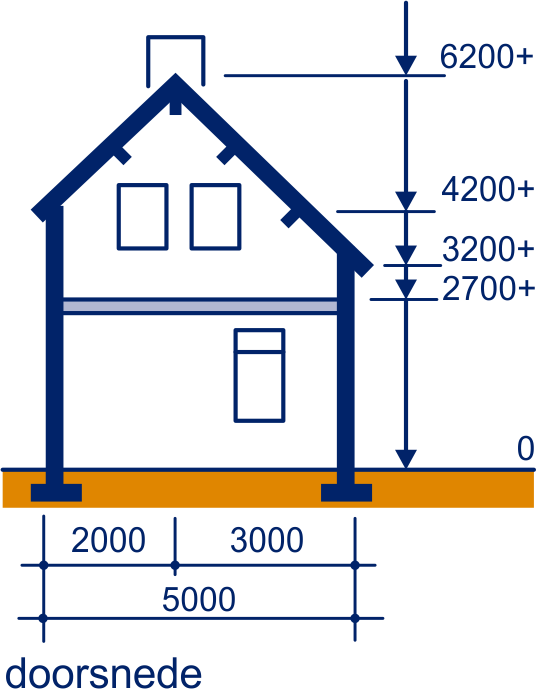
Een architect heeft een vrijstaand huis ontworpen. Het is $6$ meter breed; zie voor de overige maten, in mm, de doorsnede. Om de bouwkosten te schatten hanteert de architect de volgende vuistregel: elke m³ kost € $350$ ,- (prijs van 2014).

Op welk bedrag schat de architect de bouwkosten?

Een luciferdoosje meet $1$ bij $3$ bij $5$ cm.
We duwen het omhulsel scheef. In stand I is de opening nog rechthoekig. In stand II is de opening een parallellogram met een hoek van $60 °$ . In stand III is die hoek $45 °$ en in stand IV $30 °$ . Je kunt het doosje ook nog helemaal platdrukken, dan is de inhoud $0$ .

Bereken de inhoud binnen het omhulsel in elk van deze standen. Geef zowel de exacte antwoorden als benaderingen in mm³ nauwkeurig.

Opmerking:

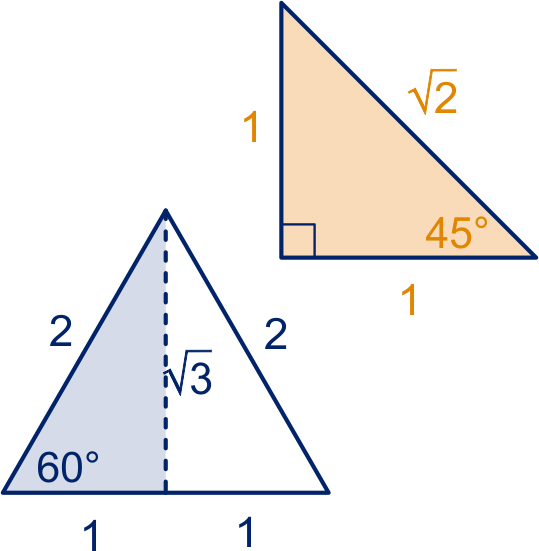
De halve gelijkzijdige driehoek heeft hoeken van $30 °$ , $60 °$ en $90 °$ ;
de "geodriehoek" heeft hoeken van $45 °$ , $45 °$ en $90 °$ .
De zijden van deze driehoeken hebben bekende verhoudingen, zie plaatje.

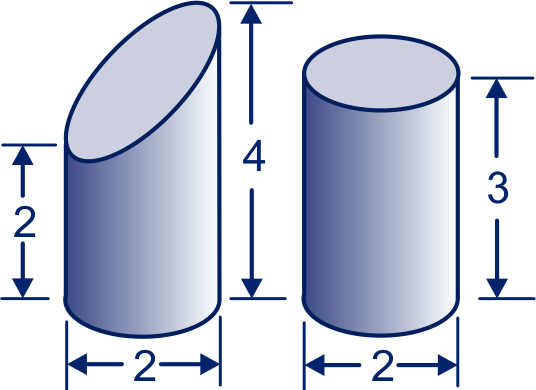
We vergelijken een scheefafgezaagde cilinder met een gewone cilinder. De afmetingen zijn hiernaast vermeld.

Leg uit dat de lichamen dezelfde inhoud hebben.
Hoe groot is die inhoud?

Hebben de cilindermantels dezelfde oppervlakte? (De mantel van een cilinder is het gebogen deel.)
Hoe groot is die oppervlakte exact?

We zagen de balk van $2$ bij $2$ bij $4$ uit figuur 1 op drie manieren scheef af, zie figuur 2.
Van drie van de verticale ribben is de lengte vermeld.

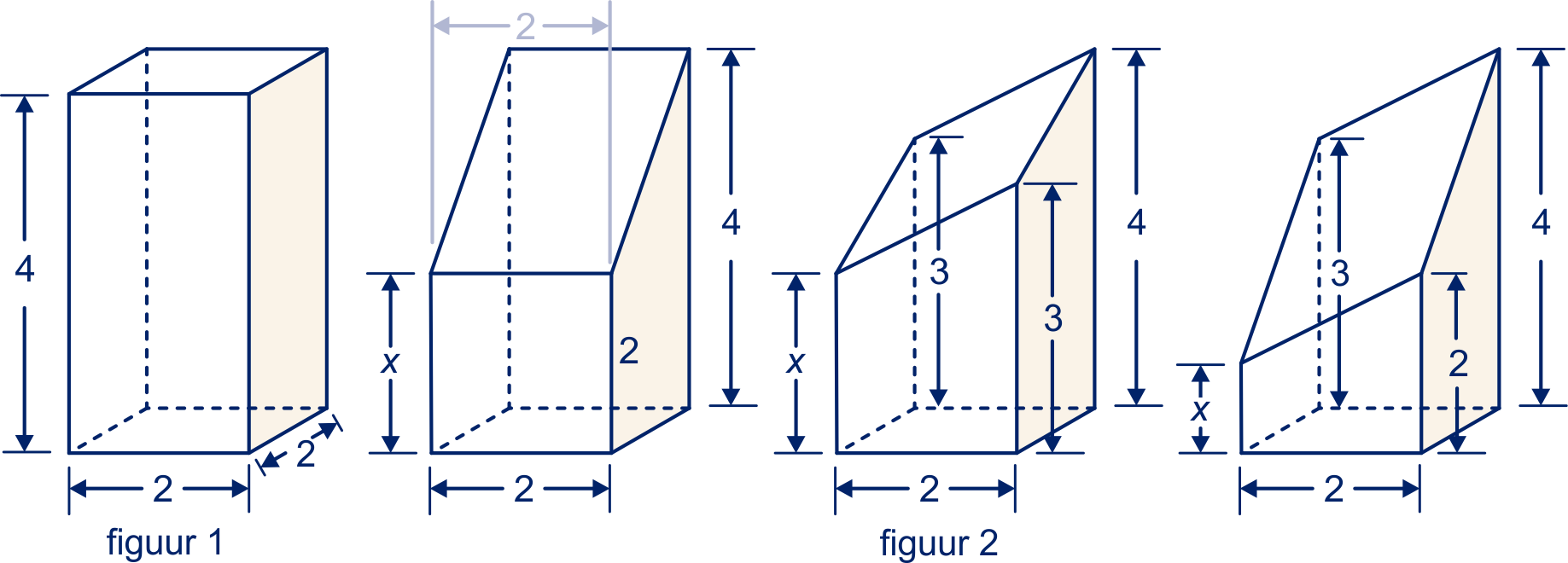
Hoe lang is de vierde verticale ribbe?

Bereken de inhoud van elk van de afgezaagde lichamen.

Bereken de hellingshoek van het zaagvlak van de eerste twee lichamen. (Bij het derde lichaam is dat veel moeilijker.)

In de oorspronkelijke balk vormen de punten op hoogte $3$ een vierkant. We doorsnijden de drie afgezaagde balken ook op hoogte $3$ .

Teken de doorsneden op ware grootte. Neem $1$ cm als eenheid.

Bereken de oppervlakte en de omtrek van deze doorsneden.