12.1 Meetkunde zonder coördinaten >

Hoofdstukken > Examentraining

In dit hoofdstuk komen de behandelde onderwerpen per paragraaf nog eens langs. Bij elk onderwerp staan een aantal oefenopgaven.
In de laatste paragraaf volgen wat complexere opgaven op examenniveau.

In deze eerste paragraaf komt aan bod hoe je lengtes van lijnstukken en grootte van hoeken berekent.

In een rechthoekige driehoek

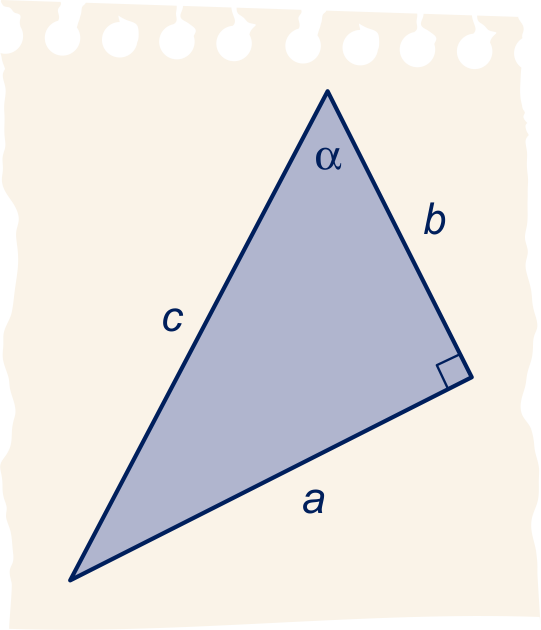
Stelling van Pythagoras
In een rechthoekige driehoek met rechthoekszijden $a$ en $b$ en schuine zijde $c$ geldt $a^{2} + b^{2} = c^{2}$ .
Het omgekeerde is ook waar: als in driehoek met zijden $a$ , $b$ en $c$ geldt: $a^{2} + b^{2} = c^{2}$ , dan is de hoek tegenover zijde $c$ recht.

Sinus, cosinus en tangens van een scherpe hoek, zeg α, hebben we als volgt gedefinieerd.
De rechthoekszijde tegenover de hoek α noemen we $a$ .
De rechthoekszijde waar α aanligt, noemen we $b$ . De schuine zijde noemen we $c$ . Dan:
$\sin (α) = \frac{a}{c}$ , $\cos (α) = \frac{b}{c}$ en $\tan (α) = \frac{a}{b}$ .
Welke rechthoekige driehoek je bij α maakt doet er niet toe.

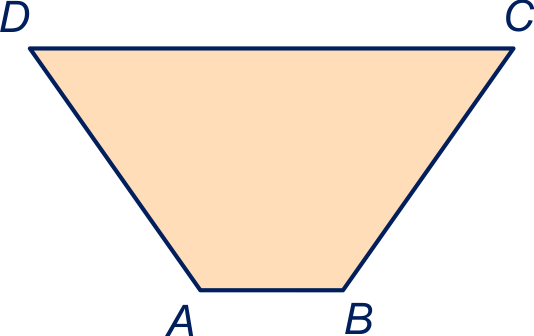
Gegeven is een gelijkbenig trapezium met: $A B = 28$ ,
$C D = 100$ en $A D = B C = 60$ .

Bereken de oppervlakte van het trapezium exact.

Bewijs dat hoek $D B C$ recht is.

Bereken de hoek waaronder de diagonalen elkaar snijden in graden nauwkeurig.

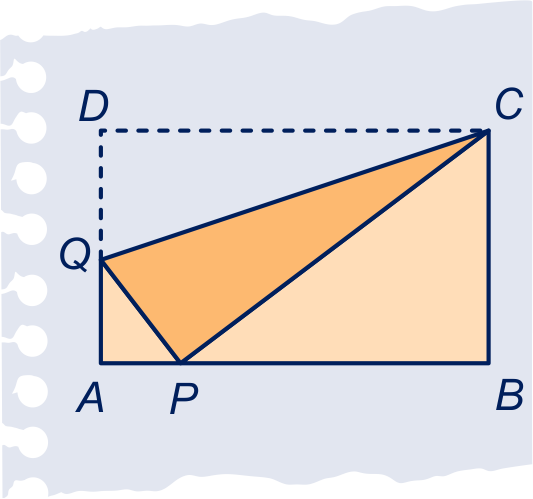
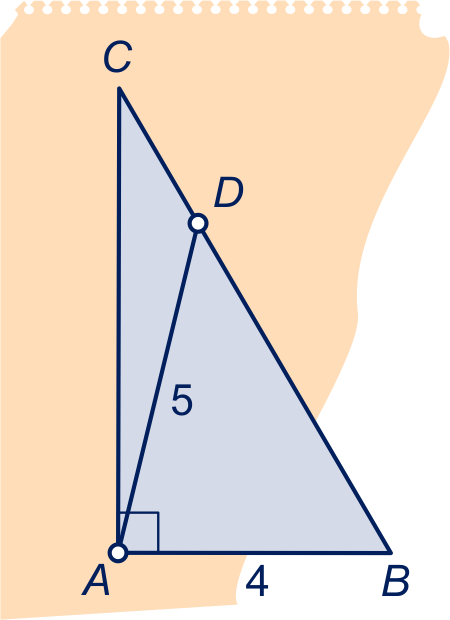
Een rechthoekig stuk papier $A B C D$ van $18$ bij $30$ , aan de voorkant licht en aan de achterkant donker oker, wordt langs lijn $C Q$ omgevouwen zó, dat hoekpunt $D$ op zijde $A B$ komt, zie figuur.
$Q$ ligt op zijde $A D$ .

Bereken $D Q$ exact.

(hint)

$C D$ en $C P$ zijn even lang.

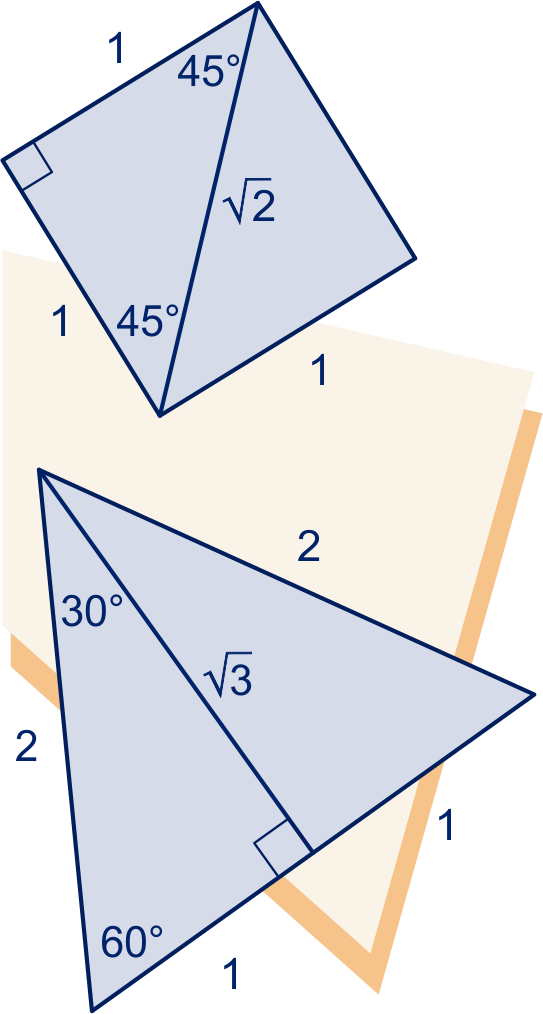
Speciale driehoeken
Bijzondere rechthoekige driehoeken zijn het halve vierkant en de halve gelijkzijdige driehoek.

In een driehoek met hoeken van $30$ , $60$ en $90$ graden verhouden de lengten der zijden zich als $1 : 2 : \sqrt{3}$ ;
In een driehoek met hoeken van $45$ , $45$ en $90$ graden verhouden de lengten der zijden zich als $1 : 1 : \sqrt{2}$ .

Hieruit volgt onmiddellijk de volgende tabel.

hoek in $°$	$30 °$	$45 °$	$60 °$
sin	$\frac{1}{2}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2} \sqrt{3}$
cos	$\frac{1}{2} \sqrt{3}$	$\frac{1}{2} \sqrt{2}$	$\frac{1}{2}$

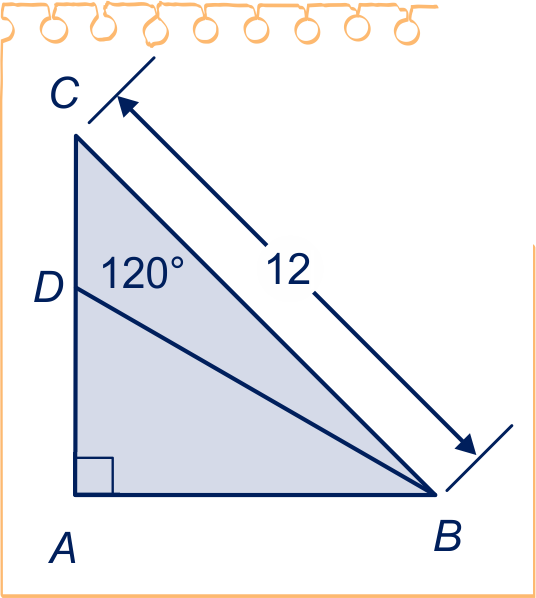
Driehoek $A B C$ is gelijkbenig rechthoekig met $B C = 12$ . Punt $D$ ligt op zijde $A C$ , zó, dat hoek $B D C = 120 °$ .

Bereken $C D$ exact.

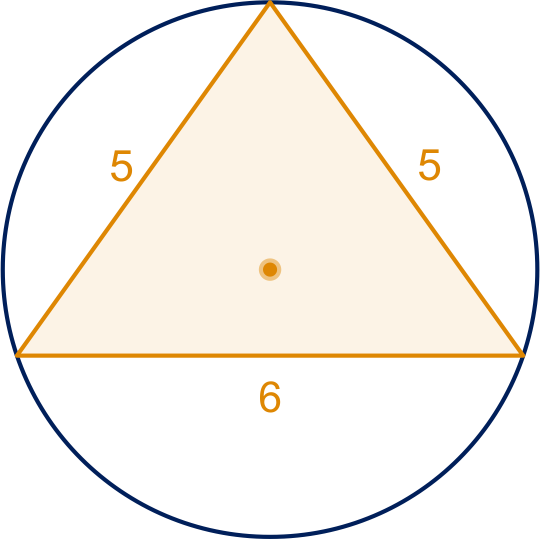
Van een driehoek zijn de zijden $5$ , $5$ en $6$ .
De straal van de omgeschreven cirkel noemen we $R$ .
Zie figuur.

Bereken de oppervlakte van de driehoek.

Laat zien dat $R^{2} = {(4 - R)}^{2} + 9$ .

Bereken $R$ .

Gelijkvormigheid

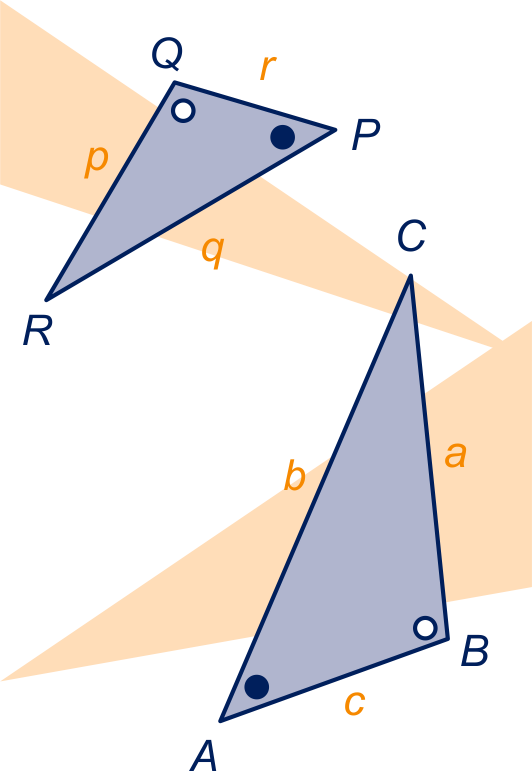
Twee driehoeken zijn gelijkvormig als de een een vergroting (of verkleining) is van de ander.
Dit is bijvoorbeeld het geval als ze twee hoeken hetzelfde hebben of als corresponderende zijden dezelfde verhouding hebben.
De driehoeken $A B C$ en $P Q R$ zijn gelijkvormig.

De corresponderende zijden zijn $a$ en $p$ (ze liggen tegenover dezelfde hoek), $b$ en $q$ (idem) en $c$ en $r$ (idem).
Dus: $\frac{a}{p} = \frac{b}{q} = \frac{c}{r}$ .
Je kunt ook zeggen: $a : b : c = p : q : r$ .

Veronderstel: de factor waarmee je driehoek $P Q R$ moet vergroten om driehoek $A B C$ te krijgen is $f$ . In klas Havo 2 heb je gezien dat de oppervlakte van driehoek $A B C$ dan $f^{2}$ keer de oppervlakte van driehoek $P Q R$ is.

Voorbeeld:

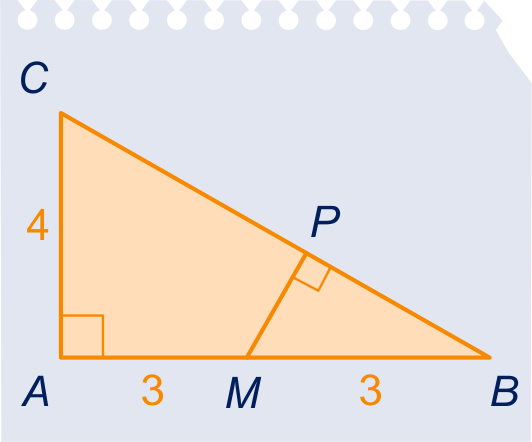
$A B C$ is een rechthoekige driehoek. $M$ is het midden van $A B$ en $P$ de loodrechte projectie van $M$ op zijde $B C$ . Verder zie figuur. $B C = \sqrt{52} = 2 \sqrt{13}$ .
Dan is driehoek $A B C$ gelijkvormig met $P B M$ , want beide driehoeken hebben een rechte hoek en ze hebben hoek $B$ gemeenschappelijk. De factor $f$ waarmee driehoek $P B M$ vergroot wordt tot driehoek $A B C$ is $f = \frac{A C}{M P} = \frac{A B}{B P} = \frac{B C}{M B} = \frac{2 \sqrt{13}}{3}$ $= \frac{2}{3} \sqrt{13}$ .
Dus $B P = \frac{6}{\frac{2}{3} \sqrt{13}} = \frac{9}{13} \sqrt{13}$ en $M P = \frac{4}{\frac{2}{3} \sqrt{13}} = \frac{6}{13} \sqrt{13}$ .
De oppervlakte van driehoek $A B C$ is $\frac{1}{2} \cdot 4 \cdot 6 = 12$ en de oppervlakte van driehoek $P B M$ is $\frac{12}{f^{2}} = 2 \frac{1}{13}$ .

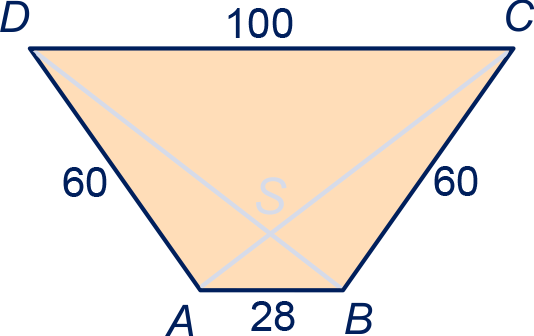
Bekijk nog eens het trapezium van opgave 1. Het snijpunt van de diagonalen noemen we $S$ .

Waarom zijn de driehoeken $A S B$ en $D S C$ gelijkvormig?

Bereken de lengte van $A S$ exact.

De diagonalen verdelen het trapezium in vier delen.

Bereken de exacte oppervlakte van elk van de vier delen.

De sinus- en de cosinusregel

Als je driehoeken geen rechte hoeken hebben, kom je vaak met de sinus- en cosinusregel verder.
Omdat in driehoeken ook stompe hoeken voorkomen, moeten we ook afspreken wat we onder de sinus, cosinus en tangens van een stompe hoek verstaan.

Afspraak

Als $α$ stomp, dan:	$\sin (α) = \sin (180 ° - α)$ ,
	$\cos (α) = ‐ \cos (180 ° - α)$ .
Verder:	$\sin (90 °) = 1$ en $\cos (90 °) = 0$ ,
	$\sin (180 °) = 0$ en $\cos (180 °) = ‐ 1$ .

Neem de tabel hieronder over en vul de exacte waarden in, zonder rekenmachine.

	$90 °$	$120 °$	$135 °$	$150 °$	$180 °$
sin
cos

Om de sinus- en cosinusregel gemakkelijk te kunnen formuleren, maken we de volgende afspraak.

Afspraak

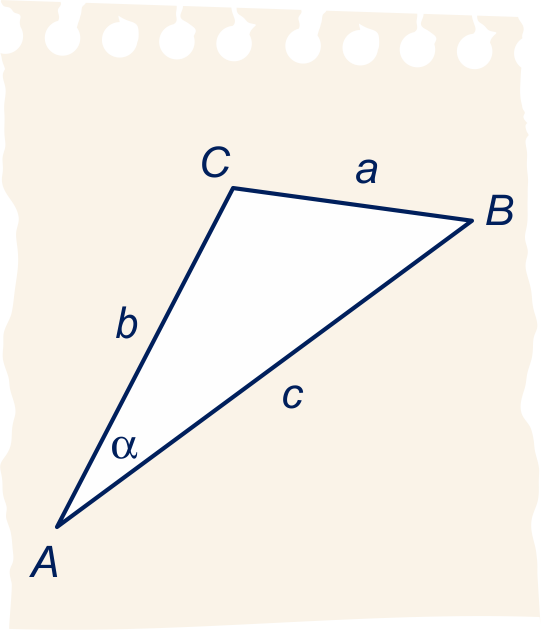
In driehoek $A B C$ noemen we

de grootte	van hoek $A$	α
	van hoek $B$	β
	van hoek $C$	γ
de lengte	van zijde $A B$	$c$
	van zijde $A C$	$b$
	van zijde $B C$	$a$

Merk op dat:
de zijde met lengte $a$ tegenover hoek $A$ ligt,
de zijde met lengte $b$ tegenover hoek $B$ en
de zijde met lengte $c$ tegenover hoek $C$ .

Sinusregel
$\frac{\sin (α)}{a} = \frac{\sin (β)}{b} = \frac{\sin (γ)}{c}$

Cosinusregel
$a^{2} = b^{2} + c^{2} - 2 b c \cdot \cos (α)$ ,
$b^{2} = a^{2} + c^{2} - 2 a c \cdot \cos (β)$ ,
$c^{2} = a^{2} + b^{2} - 2 a b \cdot \cos (γ)$ .

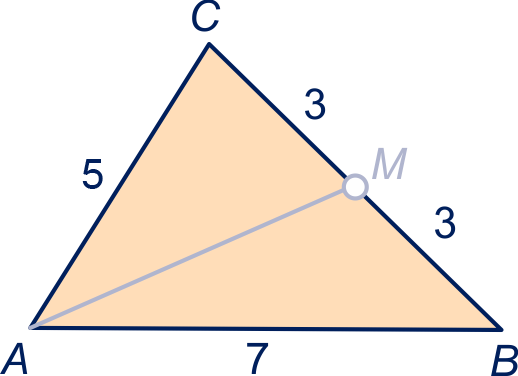
Driehoek $A B C$ heeft zijden van lengte $5$ , $6$ en $7$ . $M$ is het midden van zijde $B C$ . Zie figuur.

Bereken hoek $A B C$ in graden nauwkeurig.

Bereken $A M$ exact.

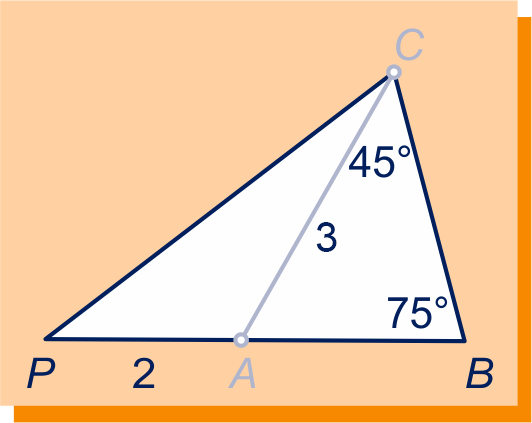
Gegevens zie figuur: $A C = 3$ , $P A = 2$ , hoek $A C B = 45 °$ en hoek $A B C = 75 °$ .

Bereken de andere zijden van driehoek $A B C$ in één decimaal nauwkeurig.

Bereken $P C$ exact.

Bereken de oppervlakte van driehoek $A P C$ exact.

Driehoek $A B C$ is een $30 - 60 - 90 -$ graden driehoek.
$A B = 4$ en op zijde $B C$ ligt een punt $D$ zó, dat $A D = 5$ , zie figuur.

Bereken $B D$ exact.

Bereken hoek $A D C$ in graden nauwkeurig.

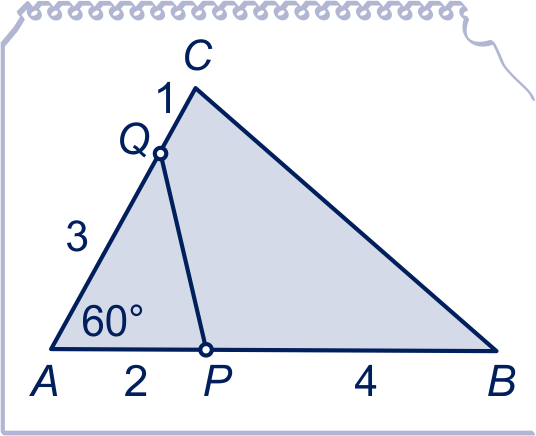
In driehoek $A B C$ geldt: hoek $B A C = 60 °$ , $A C = 4$ en $A B = 6$ .
Op zijde $A B$ ligt punt $P$ zó, dat $A P = 2$ ; op zijde $A C$ ligt punt $Q$ zó, dat $A Q = 3$ .

Toon aan dat de driehoeken $A B C$ en $A Q P$ gelijkvormig zijn.

(hint)

Spiegel driehoek $A P Q$ in de bissectrice van hoek $A$ .

Lijn $P Q$ verdeelt driehoek $A B C$ in twee stukken.

Hoe verhouden zich de oppervlakten van de twee stukken?

$P Q = \sqrt{7}$ .

Toon dat aan.

Hoe lang is dus $B C$ ?

Bereken hoek $A B C$ in graden nauwkeurig.

Bereken hoek $C Q P$ in graden nauwkeurig.

Cirkels

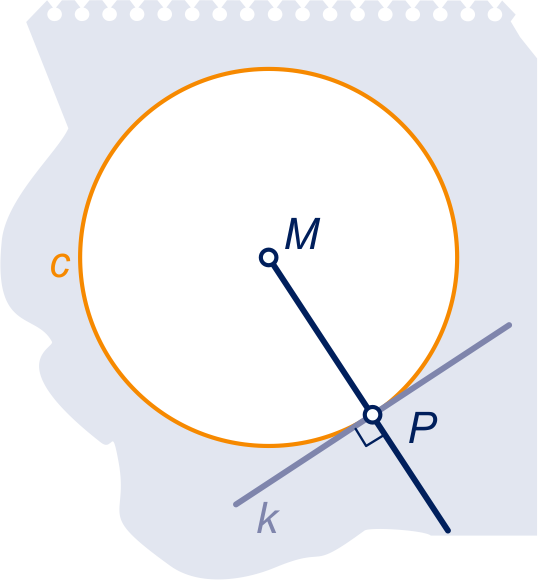
Een cirkel $c$ raakt een lijn $k$ als $c$ en $k$ precies één punt, het raakpunt, gemeen hebben.
Als $c$ middelpunt $M$ heeft en het raakpunt $P$ is, dan staat lijn $M P$ loodrecht op $k$ .

Twee cirkels raken elkaar als ze in een gemeenschappelijk punt dezelfde raaklijn hebben.

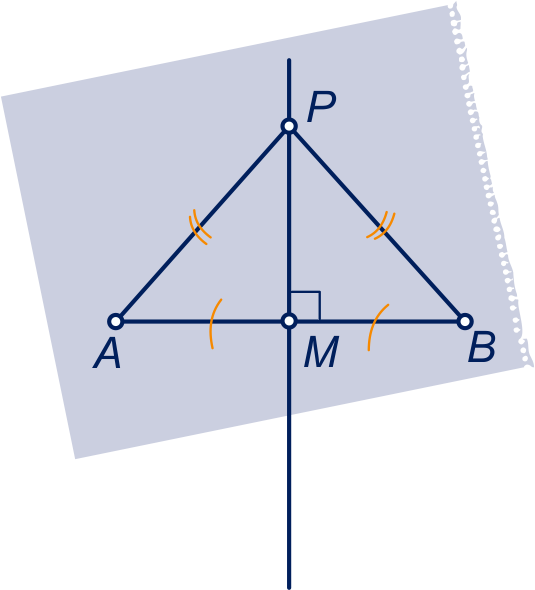
Gegeven twee punten $A$ en $B$ .
De punten die even ver van $A$ als van $B$ liggen, vormen de middelloodlijn van lijnstuk $A B$ . Deze lijn gaat door het midden van lijnstuk $A B$ en staat loodrecht op lijn $A B$ .

Opmerking:

Het middelpunt van een cirkel die door twee punten $P$ en $Q$ gaat, ligt op de middelloodlijn van $P Q$ .

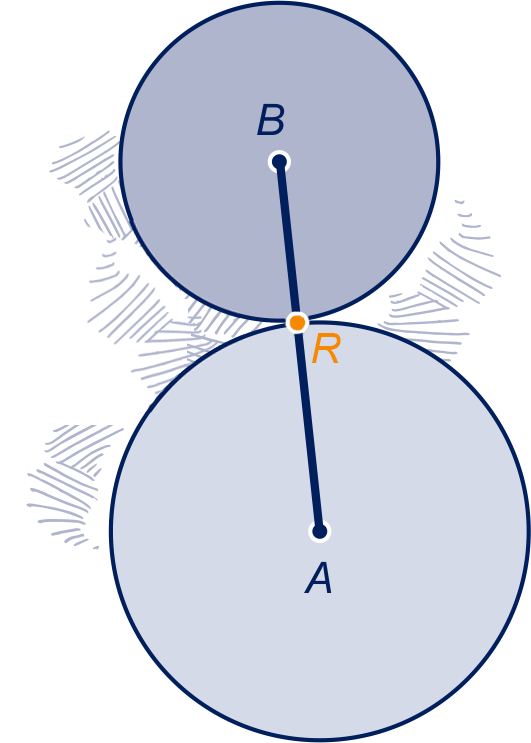
Wanneer twee cirkels elkaar raken, dan ligt het raakpunt $R$ op het verbindingslijnstuk van de middelpunten $A$ en $B$ van de twee cirkels.
De lengte van lijnstuk $A B$ is dus gelijk aan de som van de twee stralen van de cirkels.

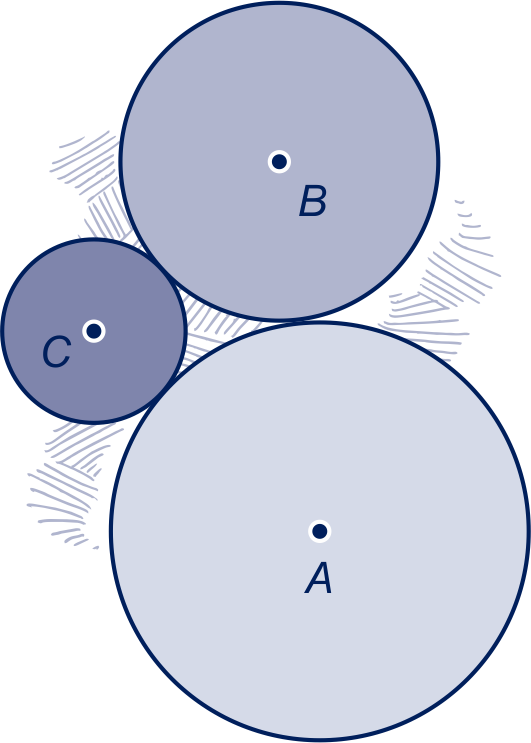
Drie cirkels met middelpunt respectievelijk $A$ , $B$ en $C$ en straal $3 \frac{1}{2}$ , $2 \frac{1}{2}$ en $1 \frac{1}{2}$ raken elkaar twee aan twee, zie figuur.

Bereken hoek $A B C$ in twee decimalen nauwkeurig.

Bereken de oppervlakte van het deel van driehoek $A B C$ dat binnen de cirkel met middelpunt $B$ ligt in één decimaal nauwkeurig.

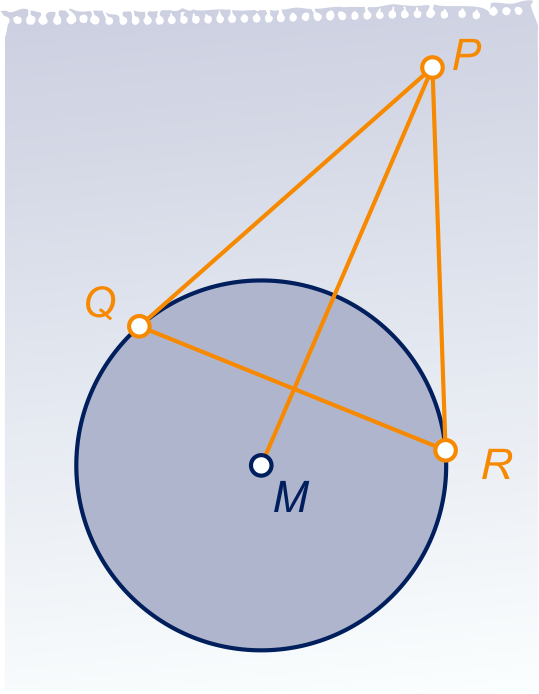
In de figuur staat een cirkel met middelpunt $M$ en straal $2 \sqrt{5}$ .
Vanuit een punt $P$ worden raaklijnen aan de cirkel getekend die de cirkel in $Q$ en $R$ raken. De afstand van $Q$ tot $R$ is $8$ .

Bereken de afstand van $M$ tot $P$ exact.

Van driehoek $A B C$ is gegeven: $a = 4$ , $b = 5$ en $c = 6$ .

Bereken $\cos (α)$ exact.

Een cirkel gaat door $B$ en raakt lijn $A C$ in $A$ .

Bereken de straal van de cirkel exact.

In een vierkant $A B C D$ met zijde $24$ zijn drie halve cirkels getekend. Punten $P$ , $Q$ en $R$ zijn de middens van deze halve cirkels. De drie halve cirkels raken elkaar.
Noem de stralen van de twee kleinere halve cirkels $x$ en $y$ . Zie figuur. In de figuur is ook lijnstuk $P Q$ getekend.

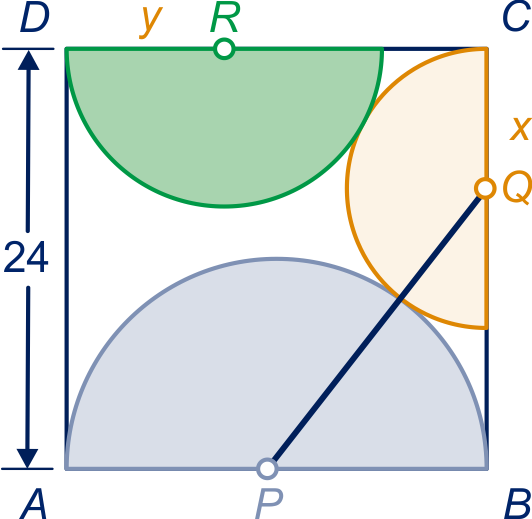
Bereken exact de lengte van straal $x$ met behulp van de stelling van Pythagoras in driehoek $B P Q$ .

Bereken exact de lengte van straal $y$ .

Een vierde halve cirkel met middelpunt op de linkerzijde van het vierkant raakt twee van de getekende halve cirkels. Noem de straal van deze cirkel $r$ .
De waarde van $r$ kun je uitrekenen door tegelijkertijd twee keer de stelling van Pythagoras toe te passen.

Leg uit dat (na vereenvoudiging) geldt
$\sqrt{r^{2} + 18 r} + \sqrt{r^{2} + 24 r} = 24$ .

Bereken de waarde van $r$ afgerond op 2 decimalen.

Bas gaat vissen. Hij heeft een hengel van $2,6$ meter lengte. Hij denkt dat hij het meeste succes heeft wanneer hij de hengel onder een hoek van $30 °$ houdt.
Na een tijdje zo gezeten te hebben zonder iets te vangen, wordt hij moe. Hij steekt $10$ cm van het uiteinde van de hengel op $1,5$ meter vanaf de waterkant in de grond en ondersteunt de hengel met een stok precies op de waterkant.
De oever is $10$ cm hoger dan het wateroppervlak. Hieronder is daarvan een schematische tekening gemaakt.

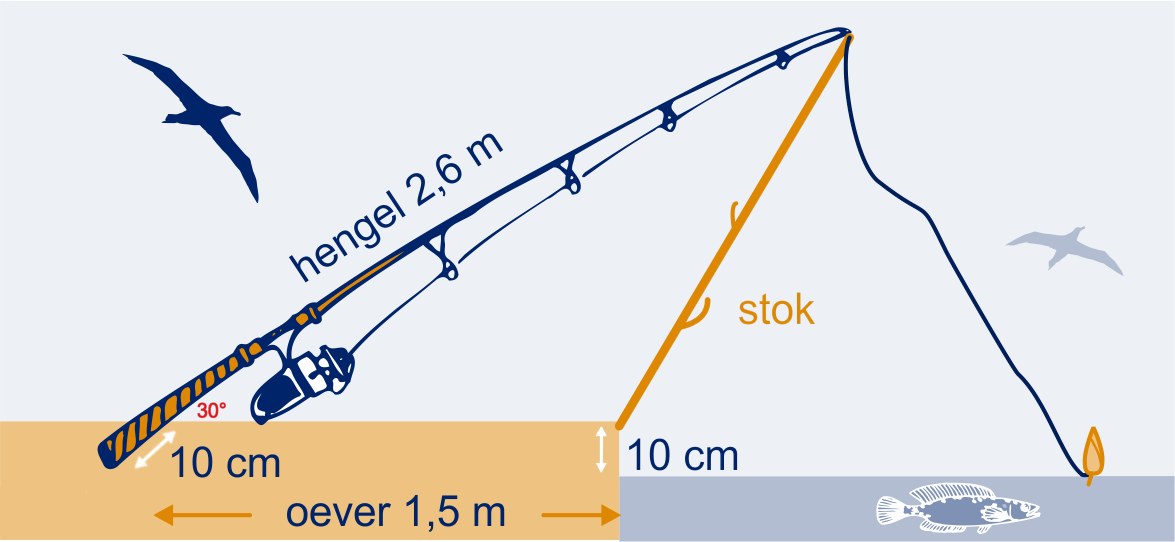
De hoogte van het puntje van de hengel boven het wateroppervlakte is $135$ cm.

Toon dit met een berekening aan.

Bereken in cm nauwkeurig de lengte van de stok.

Bereken de hoek tussen de stok en de oever. Rond je antwoord af op een geheel aantal graden.

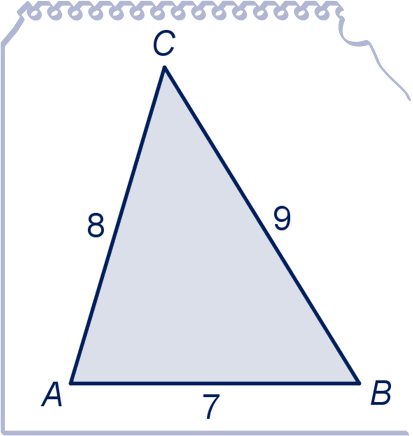
Van een driehoek $A B C$ zijn de zijden $7$ , $8$ en $9$ .

Bereken exact de oppervlakte van de driehoek.

(hint)

Teken het hoogtelijstuk uit $A$ ; deze verdeelt zijde $B C$ in stukken met lengte $x$ en $9 - x$ ; dan twee keer Pythagoras.