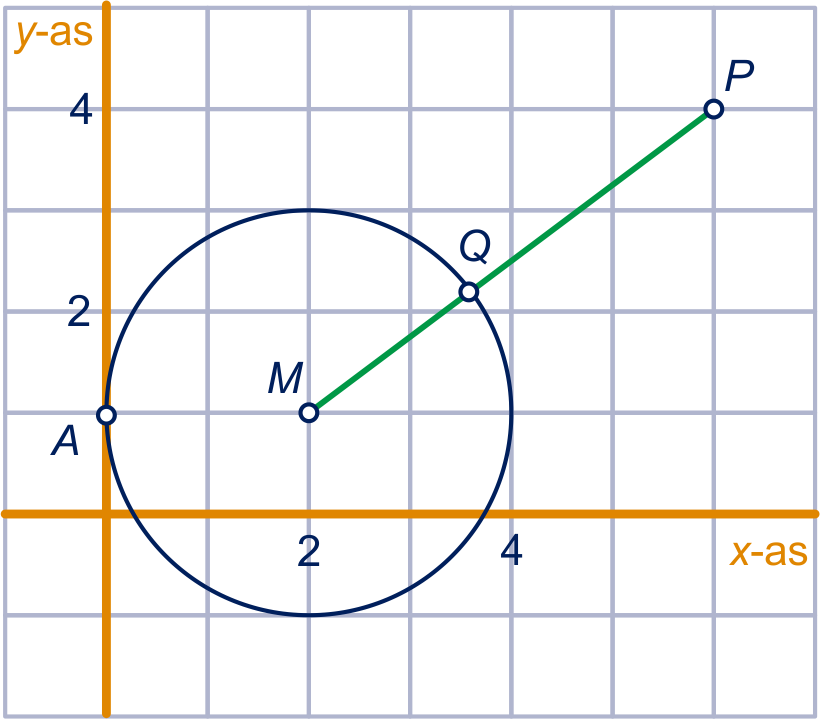
.
Dus het middelpunt van de cirkel is en de straal is , dus de afstand van tot de cirkel is .
, dus de afstand van tot de cirkel is .
De cirkels met middelpunt en stralen en .
, waarbij het midden van is.
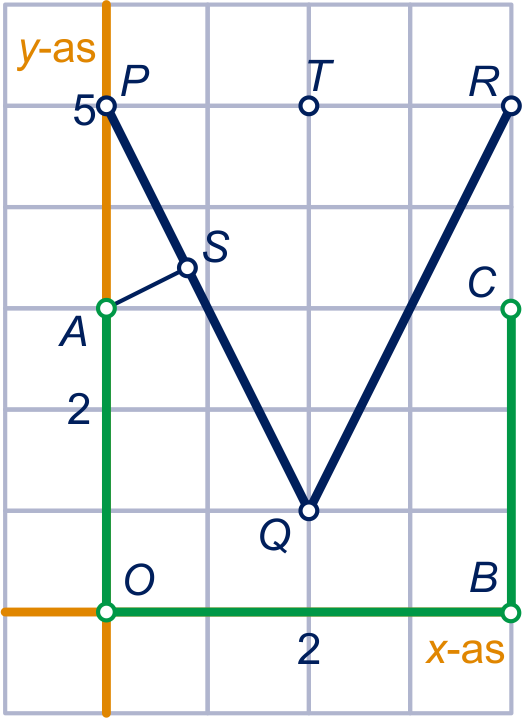
Het loodlijnstuk vanuit op lijn , Het loodlijnstuk vanuit op lijn en .
De driehoeken
en zijn gelijkvormig, want
ze hebben beide een rechte hoek en de hoeken en
zijn even groot (z-hoeken).
De vergrotingsfactor is ,
dus .
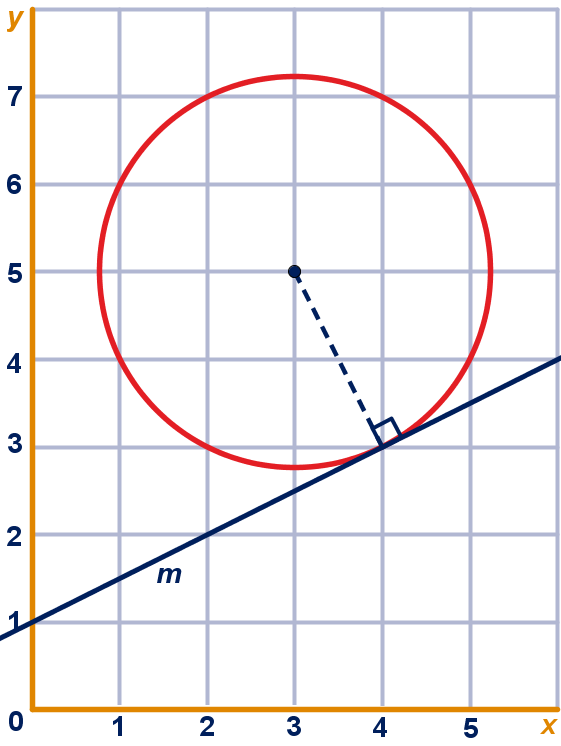
Zie figuur 1 hieronder. Teken de loodrechte projectie van op . Het snijpunt van lijn met de cirkel noemen we . Lijnstuk is het kortste verbindingslijnstuk van met de cirkel.
Zie figuur 2. is het punt
en
is het snijpunt van lijnstuk
met de cirkel.
is het kortste verbindingslijnstuk van de -as en de cirkel,
en
.
Zie figuur 2.
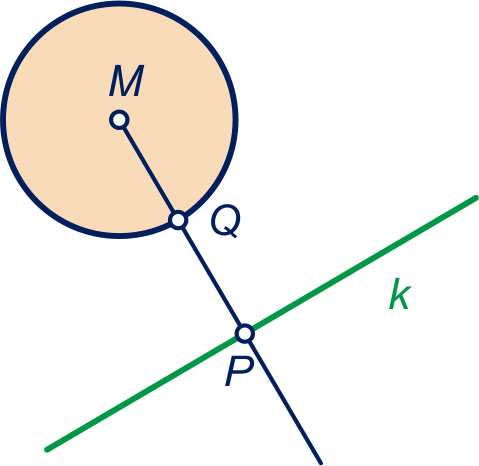
figuur 1
|
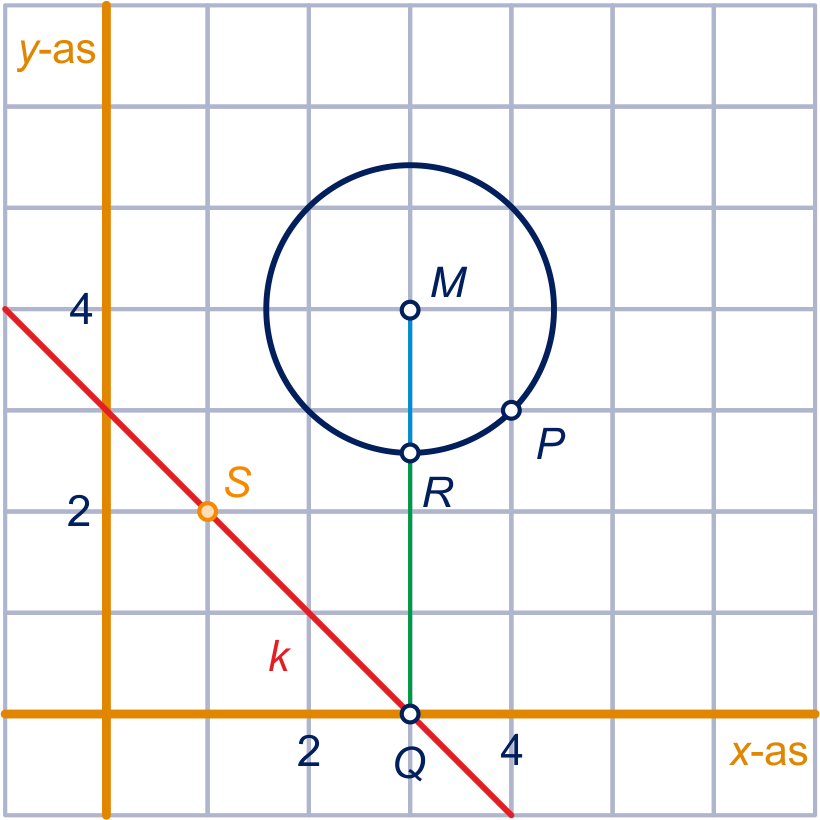
figuur 2
|
Dat is . . De afstand is .
:
de richtingscoëfficiënt van is
en
ligt op .
en
Dat is de afstand van tot , dus .
of ligt op de lijn , dus of .
De cirkel met middelpunt en straal raakt dan de lijn . Het raakpunt ligt dan op de lijn van de vorige opgave maar dan keer zo ver van als of , dus het raakpunt is of . Dan of .
Voor
invullen in geeft:
Deze vergelijking moet één oplossing hebben, dus zijn discriminant is .
of .
Het raakpunt ligt op de lijn door het middelpunt loodrecht op de lijnen met vergelijking , dus op de lijn met vergelijking . Deze lijn snijden met de cirkel geeft de snijpunten: en . Dus of ligt op de lijn, dus of .
De cirkel met vergelijking
heeft straal
en middelpunt .
De cirkel met middelpunt en straal
moet dan de lijn raken.
Als je voor
in de vergelijking invult moet de vergelijking in die je krijgt discriminant hebben.
,
dus , dus
of
.
Het kan ook anders.
De punten op de cirkel die het dichtst bij de lijn liggen, liggen op de lijn door loodrecht op de lijn
, dus op lijn met vergelijking
. Deze lijn snijdt de
cirkel in de punten en
. De punten op die
keer zo ver van
afliggen, dus
of moeten dan op liggen, dus of
.
Als je voor
in de vergelijking invult moet de discriminant
zijn.
,
dus
, dus
.
Vergelijking van de loodlijn door het middelpunt:
.
Snijpunt van de twee lijnen uitrekenen: .
De straal is de afstand tussen en , ofwel .
