Groei

In de periode $1900-1927$ werd de Nederlandse bevolking $1 \frac{1}{2}$ keer zo groot.
In de periode $1927-1991$ werd de bevolking $2$ keer zo groot.

Hoeveel keer zo groot werd de bevolking in de periode $1900-1991$ ?

In $1991$ had Nederland ongeveer $15$ miljoen inwoners.

Hoeveel inwoners had Nederland ongeveer in $1900$ ?

Groeiprincipe
Als een hoeveelheid eerst $a$ keer zo groot wordt en vervolgens nog eens $b$ keer zo groot, wordt de hoeveelheid in totaal $a \cdot b$ keer zo groot.

Je hebt vier grootouders; dat noemen we de ouders-van-twee-generaties-terug.

Hoeveel voorouders heb jij van-zes-generaties-terug?

Als je een generatie terug gaat, wordt het aantal voorouders twee keer zo groot. Zo zou je door kunnen rekenen tot het begin van onze jaartelling.

Hoeveel voorouders van jou zouden er volgens deze manier van rekenen geleefd hebben, toen Christus geboren werd? Schat dat aantal.

Waarschijnlijk kwam je berekening uit op een waanzinnig groot aantal voorouders. Dat kan natuurlijk niet.

Kun je uitleggen hoe het komt dat je berekening in het vorige onderdeel een veel te groot aantal geeft?

Bacteriën vermenigvuldigen zich door deling: ze breken middendoor. Elke helft groeit weer tot de oorspronkelijke grootte, en breekt dan weer in tweeën. Uit één enkele bacterie kan op deze manier in korte tijd een enorm aantal bacteriën ontstaan. Daarvoor is wel nodig, dat er voldoende vocht en voedsel aanwezig is en dat de temperatuur gunstig is (voor de meeste soorten $25 ° C$ ).

We bekijken een kolonie bacteriën. We veronderstellen dat het groei- en delingsproces één uur duurt en dat er om $12.00$ uur $1$ mg bacteriën is.
Het aantal bacteriën na $t$ uur is $B (t)$ milligram.

Maak een tabel:

$t$	$0$	$1$	$2$	$3$	$4$
$B (t)$	$1$	$2$

Teken de vijf punten van de grafiek van de functie $B$ die je in het vorige onderdeel berekend hebt.
Zet $t$ horizontaal uit en $B (t)$ verticaal.

Omdat de groei van het aantal bacteriën geleidelijk verloopt, krijg je een goed beeld van het aantal bacteriën op elk moment door de getekende punten met een vloeiende lijn te verbinden.

Geef een formule voor $B (t)$ als $t$ een geheel getal is.

$2^{3}$ is het aantal mg bacteriën $3$ uur na $12.00$ uur.
Onder $2^{2 \frac{1}{2}}$ zullen we verstaan het aantal mg bacteriën $2 \frac{1}{2}$ uur na $12.00$ uur.

Lees uit de grafiek af hoe groot $2^{2 \frac{1}{2}}$ ongeveer is.

De groei van het aantal bacteriën is niet lineair. Dat zie je ook aan de formule $B (t) = 2^{t}$ .
Omdat de invoer-variabele $t$ in de exponent voorkomt, spreken we van exponentiële groei.

Op de GR kun je gemakkelijk de exponentiële rij 1, 2, 4, 8, 16, ... maken. Kijk in de gebruiksaanwijzing of vraag je docent hoe dat moet.

Rekenregels voor machten

$2^{5} = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2$ en $2^{3} = 2 \cdot 2 \cdot 2$ .
Schrijf de antwoorden op de volgende vragen als macht van $2$ .

Hoe groot is $2^{5} \cdot 2^{3}$ ?

Hoe groot is $2^{5} : 2^{3}$ ?

Hoe groot is ${(2^{5})}^{3}$ ?

Het aantal bacteriën wordt elke $2$ uur $2^{2}$ keer zo groot, elke $3$ uur $2^{3}$ keer zo groot en elke $5$ uur $2^{5}$ keer zo groot,

Wat is het verband tussen deze drie groeifactoren?

Het aantal bacteriën wordt elke $p$ uur $2^{p}$ keer zo groot, elke $q$ uur $2^{q}$ keer zo groot en elke $p + q$ uur wordt het $2^{p + q}$ keer zo groot.

Wat is het verband tussen deze drie groeifactoren?

Wat is het verband tussen $2^{p}$ , $2^{q}$ en $2^{p - q}$ ?

Het aantal bacteriën wordt elke $3$ uur $2^{3}$ keer zo groot. In $12$ uur (dat is $4$ periodes van $3$ uur) wordt het $2^{12}$ keer zo groot.

Wat is het verband tussen deze twee groeifactoren?

Het aantal bacteriën wordt elke $p$ uur $2^{p}$ keer zo groot. In $p \cdot q$ uur (dat is $q$ periodes van $p$ uur) wordt het $2^{p \cdot q}$ keer zo groot.

Wat is het verband tussen deze twee groeifactoren?

Schrijf als macht van $2$ .

$2^{7} \cdot 2^{5}$	$2^{7} : 2^{5}$	${(2^{7})}^{5}$
$2 \cdot 2^{7}$	$2^{7} : 2$	$1$

$2^{4} = 2 \cdot 2 \cdot 2 \cdot 2$ en $5^{4} = 5 \cdot 5 \cdot 5 \cdot 5$

Hoe groot is $2^{4} \cdot 5^{4}$ ?

Wat is het verband tussen $a^{p}$ , $b^{p}$ en ${(a \cdot b)}^{p}$ ?

Rekenregels voor machten

$a^{p} \cdot a^{q} = a^{p + q}$
$a^{p} : a^{q} = a^{p - q}$
${(a^{p})}^{q} = a^{p \cdot q}$
${(a \cdot b)}^{p} = a^{p} \cdot b^{p}$

Deze regels gelden voor alle positieve getallen $a$ , $b$ , $p$ en $q$ , waarbij $p$ en $q$ geheel zijn en $p > q$ .
Regel 1 wordt wel de hoofdeigenschap voor het rekenen met machten genoemd.

Rekenregels toepassen

Vereenvoudig met behulp van deze regels:

$\frac{x^{5} \cdot x^{3}}{x^{2} \cdot x^{4}}$

$\frac{{(y^{5})}^{3}}{{(y^{2})}^{4}}$

$\frac{{(a^{2})}^{5} \cdot a^{3}}{a^{13}}$

$\frac{{(p q)}^{5}}{p^{2} q^{3}}$

$\frac{x^{3} \cdot 64 x^{2}}{{(2 x)}^{5}}$

$\frac{{(3 y^{2})}^{4}}{81 y^{3}}$

$\frac{{({(p^{2})}^{3})}^{4}}{p^{2} \cdot p^{3} \cdot p^{4}}$

$\frac{{(a^{2} b)}^{3}}{a^{5} b}$

Voorbeeld:

$8 \cdot 2^{k} = 2^{3} \cdot 2^{k} = 2^{3 + k}$

Schrijf zo ook als één macht van $2$ ; $k$ en $m$ zijn positieve gehele getallen.

$32 \cdot 2^{k}$

$2 \cdot 2^{k}$

$2^{k} \cdot 2^{k}$

$8^{k}$

$16^{k} \cdot 32^{k}$

$2^{k} \cdot 4^{m}$

$\frac{32}{2^{k}}$

$\frac{2^{k}}{2}$

$\frac{2^{k + 1}}{2^{k - 1}}$

$\frac{8^{k}}{8}$

$\frac{32^{k}}{16^{k}}$

$\frac{4^{m}}{2^{k}}$

Onderzoek welke van de volgende formules juist zijn voor elk positief geheel getal $n$ .

$3 \cdot 9^{n} = 27^{n}$	$2^{n} + 2^{n} = 2^{2 n}$
$3 \cdot 9^{n} = 3^{2 n + 1}$	$2^{n} + 2^{n} = 2^{n + 1}$
$\frac{4^{n}}{8} = {(\frac{1}{2})}^{n}$	$3^{n} + 3^{n} + 3^{n} = 3^{n + 1}$

Maak de onjuiste formules juist door ze een klein beetje te veranderen.

Gebroken exponenten

We gaan weer verder met de bacteriekolonie die zich elk uur verdubbelt. De deling van de bacteriën vindt natuurlijk niet precies op de hele uren plaats. De ene bacterie zal zich eerder delen dan de andere. We mogen wel aannemen dat het delingsproces goed gespreid is in de tijd. We willen nu weten hoeveel keer zo groot het aantal bacteriën per half uur wordt.

Anneke denkt dat het aantal bacteriën elk half uur $1 \frac{1}{2}$ keer zo groot wordt.

Laat zien dat dat niet strookt met het gegeven dat het aantal bacteriën per uur twee keer zo groot wordt.

Anneke doet een nieuwe poging: het aantal bacteriën wordt elk half uur $1,4$ keer zo groot.

Laat zien dat ook dat niet klopt.

Hoeveel keer zo groot wordt het aantal bacteriën per half uur? Zoek dat getal in drie decimalen nauwkeurig.

Het gezochte getal uit de vorige vraag noemen we de groeifactor per half uur.
Noemen we deze groeifactor $x$ , dan is de groeifactor per uur $x \cdot x = x^{2}$ .
Dus: $x = \sqrt{2} \approx 1,4142...$ .

Zoek met je rekenmachine wat de groeifactor per kwartier is, in drie decimalen.
Zoek ook de groeifactor per $20$ minuten (dat is $\frac{1}{3}$ uur).

Betekenis van $2^{\frac{1}{3}}$
Een bacteriekolonie wordt elk uur $2$ keer zo groot.
Dan wordt de kolonie elke $20$ minuten $2^{\frac{1}{3}}$ keer zo groot.
( $20$ minuten is $\frac{1}{3}$ uur.)

Betekenis van $2^{\frac{4}{5}}$
Een bacteriekolonie wordt elk uur $2$ keer zo groot.
Dan wordt de kolonie elke $48$ minuten $2^{\frac{4}{5}}$ keer zo groot.
( $48$ minuten is $\frac{4}{5}$ uur.)

Zeg precies wat de betekenis is van $6^{\frac{2}{3}}$ in termen van de groei van een bacteriekolonie.
Teken op de GR de grafiek van $y = 6^{x}$ .
Lees uit de grafiek af hoe groot $6^{\frac{2}{3}}$ ongeveer is.
Bereken met de rekenmachine de derde macht van dat getal.
Leg met behulp van regel 3 uit dat ${(6^{\frac{2}{3}})}^{3} = 36$ .

Dezelfde opdracht voor $6^{1 \frac{1}{3}}$ .
Hoe groot is ${(6^{1 \frac{1}{3}})}^{3}$ (zonder rekenmachine)?

Het kwadraat van $x^{\frac{1}{2}}$ is $x$ , dus $x^{\frac{1}{2}} = \sqrt{x}$ ;
de derde macht van $x^{\frac{1}{3}}$ is $x$ , dus $x^{\frac{1}{3}} = \sqrt[3]{x}$ ;
de vierde macht van $x^{\frac{1}{4}}$ is $x$ , dus $x^{\frac{1}{4}} = \sqrt[4]{x}$ .

De $n$ -de macht van $x^{\frac{1}{n}}$ is $x$ , dus $x^{\frac{1}{n}} = \sqrt[n]{x}$ .

In de vorige opgave heb je ook gezien: $6^{\frac{2}{3}} = \sqrt[3]{6^{2}}$ en $6^{\frac{4}{3}} = \sqrt[3]{6^{4}}$ .
Verder zou volgens regel 1 moeten gelden: $\sqrt[3]{6} \cdot \sqrt[3]{6} = 6^{\frac{1}{3}} \cdot 6^{\frac{1}{3}} = 6^{\frac{2}{3}}$ enzovoort.
We maken dus de volgende afspraak.

Afspraak
Voor alle positieve getallen $a$ , $p$ en $q$ met $p$ en $q$ geheel geldt:
$a^{\frac{p}{q}} = \sqrt[q]{a^{p}} = {\sqrt[q]{a}}^{p}$ .

Voorbeeld:

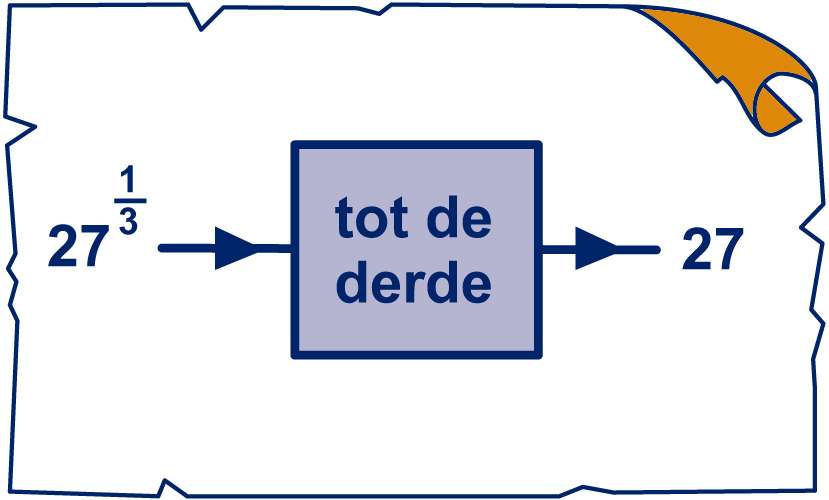
Soms komt een macht met een gebroken exponent mooi uit.
$27^{\frac{1}{3}}$ : de derde macht van dit getal is $27$ . Dus moet dat getal wel $3$ zijn!
We kennen nu ook $27^{\frac{2}{3}}$ , als volgt: $27^{\frac{2}{3}} = {(27^{\frac{1}{3}})}^{2} = 3^{2} = 9$ .

Bereken op deze manier ook zonder rekenmachine de volgende machten. Je kunt natuurlijk wel je rekenmachine gebruiken om je antwoord te controleren.

$1000^{\frac{1}{3}}$ , $1000^{\frac{2}{3}}$ , $16^{\frac{1}{4}}$ , $16^{\frac{3}{4}}$ , $49^{\frac{1}{2}}$ , $49^{1 \frac{1}{2}}$

Rekenen met gebroken exponenten

Bereken zonder rekenmachine:
$64^{\frac{1}{2}}$ , $64^{\frac{1}{3}}$ , $64^{\frac{1}{6}}$ , $64^{\frac{5}{6}}$ .
Leg uit hoe je hieraan komt.

Test zonder rekenmachine of de regels 1, 2, 3 en 4 ook voor gebroken exponenten gelden in de volgende gevallen:

$64^{\frac{1}{2}} \cdot 64^{\frac{1}{3}} = 64^{\frac{1}{2} + \frac{1}{3}}$
$64^{\frac{1}{2}} : 64^{\frac{1}{3}} = 64^{\frac{1}{2} - \frac{1}{3}}$
${(64^{\frac{1}{2}})}^{\frac{1}{3}} = 64^{\frac{1}{2} \cdot \frac{1}{3}}$
$64^{\frac{1}{3}} \cdot 1000^{\frac{1}{3}} = {(64 \cdot 1000)}^{\frac{1}{3}}$

Voorbeeld:

In het volgende gebruiken we de rekenregels voor machten met gebroken exponent.
${(a^{\frac{1}{3}})}^{7} = a^{\frac{7}{3}}$ (Regel 3)
$a \cdot a^{\frac{1}{2}} = a^{1 \frac{1}{2}}$ (Regel 1)
Dus: $\frac{{(a^{\frac{1}{3}})}^{7}}{a \cdot a^{\frac{1}{2}}} = a^{\frac{7}{3} - 1 \frac{1}{2}} = a^{\frac{5}{6}}$ (Regel 2 en het voorgaande)

Vereenvoudig als in het voorbeeld.

$\frac{{(a^{4})}^{\frac{1}{2}}}{{(a^{\frac{1}{4}})}^{5}}$	$\frac{b^{3} \cdot b^{\frac{1}{3}}}{{(b^{\frac{1}{2}})}^{6}}$
$\frac{{(c^{12})}^{\frac{2}{3}}}{c^{\frac{1}{2}} \cdot c^{\frac{1}{3}} \cdot c^{\frac{1}{6}}}$	$\frac{{(d^{\frac{4}{3}})}^{\frac{3}{2}}}{{(d^{\frac{2}{5}})}^{\frac{5}{2}}}$

Voorbeeld:

$\sqrt[3]{x^{4}} = {(x^{4})}^{\frac{1}{3}} = x^{\frac{4}{3}}$

Schrijf zo ook zonder worteltekens:

$\sqrt{a^{3}}$

$\sqrt[3]{b^{2}}$

$\sqrt{\sqrt{c}}$

$\sqrt[3]{\sqrt{d^{5}}}$

Leg uit dat voor elke $x > 0$ geldt: $x^{1 \frac{1}{2}} = x \sqrt{x}$ .

Teken op de GR in één window met $0 < x \leq 2$ de grafieken van $y = x$ , $y = x^{1 \frac{1}{2}}$ en $y = x^{2}$ .

Schrijf zonder worteltekens:

$x^{2} \sqrt{x}$

$x \sqrt[3]{x}$

$\frac{\sqrt[4]{x^{7}}}{x}$

$\frac{x}{\sqrt[3]{x}}$

Er draaien acht planeten om de zon. Onze aarde doet $1$ jaar over één omloop. Mercurius en Venus doen korter over een rondje, de andere planeten doen er langer over.
Algemeen: hoe verder een planeet van de zon staat, des te langer is zijn omlooptijd. Aan de astronoom Johannes Kepler (1571-1630) danken we de volgende formule:
$T = 0,2 R^{1 \frac{1}{2}}$ . Hierin is $R$ de afstand tot de zon in miljoenen km en is $T$ de omlooptijd in dagen.

De aarde is (gemiddeld) $149,5$ miljoen km van de zon verwijderd.

Bereken hiermee de omlooptijd. Klopt het redelijk?

Saturnus is veel verder van de zon verwijderd dan de aarde: $1427$ miljoen km.

Bereken de omlooptijd van Saturnus in jaren.

Het warmteverlies van een dier hangt af van zijn huidoppervlakte: via een grotere huid gaat meer warmte verloren dan via een kleinere huid. De warmteproductie hangt af van zijn volume: een groot dier produceert meer warmte dan een klein dier. Biologen vergelijken daarom de huidoppervlakte $H$ (in $m^{2}$ ) met het lichaamsgewicht $G$ (in kg). Het verband tussen $H$ en $G$ wordt gegeven door de formule $H = c \cdot G^{\frac{2}{3}}$ . De constante $c$ hangt af van de vorm van het dier en is dus per diersoort verschillend. Een paar voorbeelden:
$c_{koe} = 0,09$ , $c_{aap} = 0,12$ , $c_{egel} = 0,075$ , en $c_{muis} = 0,09$ .
Voor een koe en een muis geldt dus: $H = 0,09 \cdot G^{\frac{2}{3}}$ . Een koe weegt gemiddeld $500$ kg, een muis $0,05$ kg.

Bereken de huidoppervlakte van een koe en van een muis.

Hoe verhouden zich de lichaamsgewichten van een koe en een muis?
En hoe de huidoppervlakten?

Stel dat van een diersoort twee formaten voorkomen. De formaten hebben dezelfde vorm, dus ook dezelfde constante $c$ . Het grote formaat is $8$ keer zo zwaar als het kleine formaat.

Hoe verhouden zich dan de huidoppervlakten van de twee formaten?

(hint)

Stel dat het gewicht van het kleine formaat

g

is. Wat zijn dan de huidoppervlaktes van beide formaten (uitgedrukt in

g

)? Laat zien dat de huidoppervlakte van het grote formaat

4

keer zo groot is als van het kleine formaat.

Dezelfde vraag als in het vorige onderdeel maar nu is het grote formaat $7$ keer zo zwaar als het kleine.

Grotere dieren kunnen gemakkelijker extreme kou verdragen dan kleine dieren.

Kun je dat gezien de formule verklaren?

Negatieve exponenten

We bekijken nog eens de bacteriekolonie die zich elk uur verdubbelt. Op een gegeven ogenblik is er een aantal bacteriën. Drie uur daarvoor waren er minder bacteriën.

Hoeveel keer zoveel?

In overeenstemming hiermee spreken we af dat $2^{‐3} = \frac{1}{8}$ .

Als je dan $3$ uur teruggaat in de tijd, wordt de kolonie $2^{‐3}$ keer zo groot.

Zeg precies wat de betekenis is van $6^{‐1,5}$ in termen van de groei van een bacteriekolonie.

Leg aan de hand van de groei van een bacteriekolonie uit dat $6^{‐1,5} \cdot 6^{‐2,3} = 6^{‐3,8}$ .

We spreken af: $g^{‐ p} = \frac{1}{g^{p}}$ , voor $g > 0$ en $p > 0$ .
In woorden: $g^{‐ p}$ en $g^{p}$ zijn elkaars omgekeerde.

Als rekenregel 1 ook geldt voor negatieve exponenten, dan moet gelden: $g^{‐ p} \cdot g^{p} = g^{0}$ .

Ga na dat dat inderdaad het geval is.

Als rekenregel 2 ook geldt voor negatieve exponenten, dan moet gelden: $g^{p} : g^{‐ p} = g^{2 p}$ .

Ga na dat dat inderdaad het geval is.

Voorbeeld:

$4^{‐2} = \frac{1}{4^{2}} = \frac{1}{16}$
$8^{‐ \frac{2}{3}} = \frac{1}{8^{\frac{2}{3}}} = \frac{1}{2^{3 \cdot \frac{2}{3}}} = \frac{1}{2^{2}} = \frac{1}{4}$

Bereken zonder rekenmachine:

$4^{‐ \frac{1}{2}}$ , $4^{‐1 \frac{1}{2}}$ , ${(\frac{1}{9})}^{‐ \frac{1}{2}}$ , ${(\frac{1}{9})}^{‐ 1 \frac{1}{2}}$ , ${0,001}^{‐ \frac{2}{3}}$ , ${0,001}^{‐ 1 \frac{2}{3}}$ , ${(\frac{2}{5})}^{‐1}$ , ${(2 \frac{1}{2})}^{‐1}$ .

Laat met behulp van regel 3 zien dat: ${(\frac{1}{g})}^{p} = g^{‐ p}$ , ( $g > 0$ ).

De opgewekte energie van een windmolen is evenredig met de derde macht van de windsnelheid. Als het "halve" kracht waait, is de energie-opbrengst nog geen $13$ % van de opbrengst bij "volle" kracht.

Laat dit algebraïsch zien.

(hint)

$P = c \cdot w^{3}$ , waarbij $c$ de evenredigheidsconstante is, $P$ de opgewekte energie en $w$ de windsnelheid. Neem aan $v$ de volle kracht van de windsnelheid.
De energieopbrengst is dan $P = c \cdot v^{3}$ .
Als $w = \frac{1}{2} v$ , dan $P = \dots$ .