1

De wijzers van een klok
We volgen de wijzers van een klok, de grote en de kleine wijzer. Onder de stand van een wijzer verstaan we het getal op de wijzerplaat dat de wijzer aanwijst.
Bijvoorbeeld: om 14.15 uur is de stand van de kleine wijzer $2 \frac{1}{4}$ en van de grote wijzer $3$ .

De stand van de grote en de kleine wijzer zijn periodieke functies.

a

Bepaal van beide functies de periode.

b

Teken voor $24$ uur de grafiek van de stand van de kleine wijzer. Zet op de horizontale as de tijd in uren en op de verticale as de cijfers van de wijzerplaat.
Teken in dezelfde figuur de grafiek van de stand van de grote wijzer.

c

Hoe vaak staan de wijzers precies op elkaar in een etmaal?

d

Bereken algebraïsch op welk tijdstip tussen 14.00 uur en 15.00 uur de wijzers precies op elkaar staan.
Geef je antwoord in minuten, seconden en honderdsten van seconden.

(hint)

Stel voor beide wijzers eerst een formule op voor de stand in deze periode

s

als functie van de tijd

t

in uren vanaf 0.00 uur.

e

Bereken in radialen hoe groot de hoek tussen de grote en kleine wijzer is van een gewone klok om 10:10 uur. Rond je antwoord af op $2$ decimalen.

(hint)

Bereken de hoek eerst in graden.

2

Hieronder staan de grafieken van twee sinusoïden.

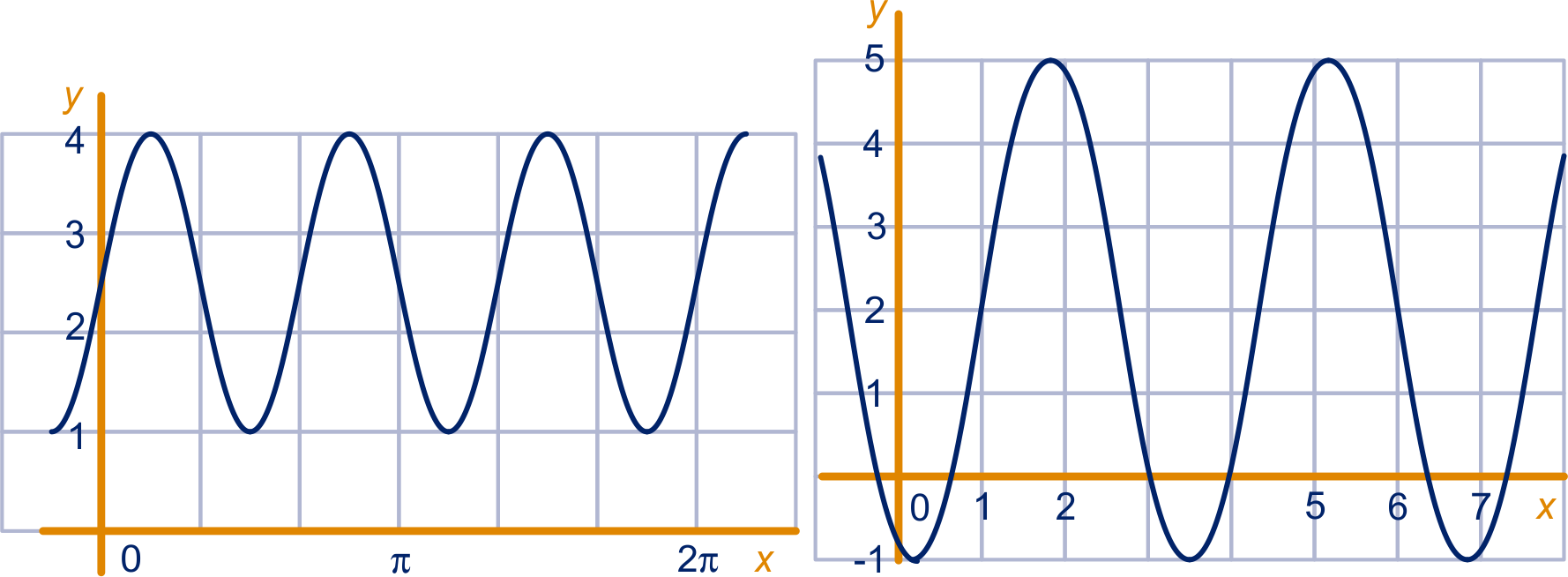
Geef bij beide grafieken een formule in de vorm
$y = a + b \sin (c (x - d))$ . Licht je formule toe.

3

Voor een animatiefilm wordt de beweging van twee manen $A$ en $B$ rond een planeet $P$ gesimuleerd. De banen worden als cirkels in één vlak gekozen. In de figuur zie je het bovenaanzicht van een situatie op een bepaald moment. $A$ en $B$ bewegen in de richting van de pijl.

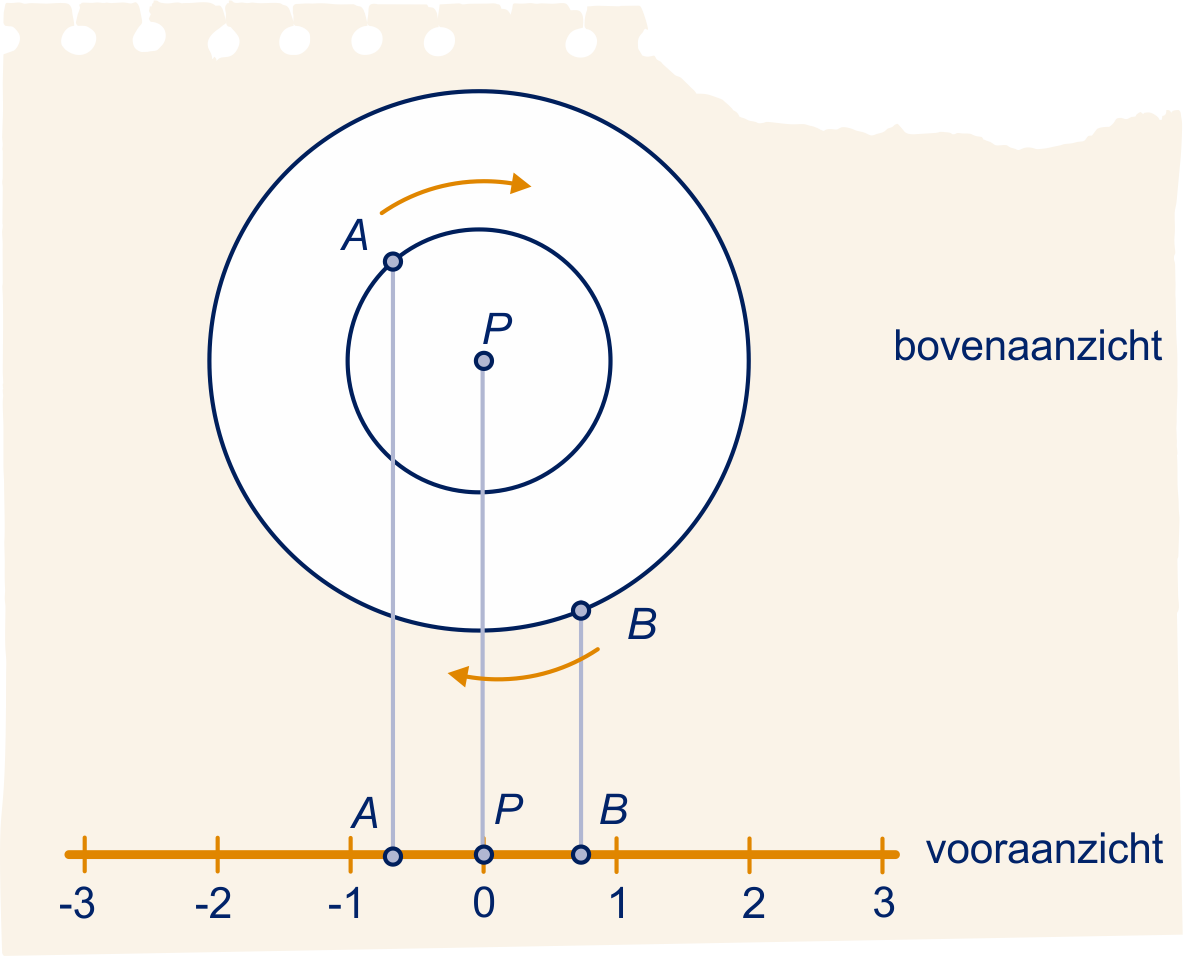
In het vooraanzicht bewegen $A$ en $B$ zich over een rechte lijn volgens de formules $x_{A} = \sin (2 π t)$ en $x_{B} = 2 \sin (π t)$ .
Hierin is $t$ de tijd in seconden en geven $x_{A}$ en $x_{B}$ de plaatsen van $A$ respectievelijk $B$ ten opzichte van $P$ aan in het vooraanzicht.

a

Teken op het werkblad in beide aanzichten de posities van $A$ en $B$ op het tijdstip $t = 0,75$ .

b

Teken in één figuur de grafieken van $x_{A}$ en $x_{B}$ als functie van $t$ voor $0 \leq t \leq 2$ .

In het bovenaanzicht zie je voortdurend de werkelijke verhouding van de afstanden $A P$ en $B P$ , namelijk $1 : 2$ , in het vooraanzicht meestal niet.

c

Op welke tijdstippen, in het interval $[0,2]$ , zie je in het vooraanzicht $B$ twee keer zo ver van $P$ als $A$ ? Beschouw alleen de situaties waarbij $A$ en $B$ aan dezelfde kant van $P$ liggen.

Er is een kunstmaan $C$ gelanceerd. Deze kunstmaan is bedoeld om $A$ van dichtbij te bestuderen. $C$ bevindt zich in dezelfde baan als $A$ en cirkelt met dezelfde snelheid als $A$ en in dezelfde richting rond $P$ . $C$ ligt $0,1$ seconde voor op $A$ .
$C$ wordt toegevoegd aan de animatiefilm.

d

Geef een formule voor de plaats $x_{C}$ in het vooraanzicht als functie van $t$

4

Fietsband
Mijn fietswiel heeft (inclusief fietsband) een doorsnede van $60$ cm. Op het loopvlak van de fietsband zit een witte stip. Tijdens het fietsen verandert de hoogte van de stip voortdurend.
$H (t)$ is de functie die de hoogte in cm van de witte stip ten opzichte van de straat beschrijft, waarbij $t$ de tijd in seconden is.
Ik fiets met een snelheid van $18$ km/uur.

a

Bereken exact de periode van $H$ in seconden. Geef je antwoord ook met $2$ decimalen.

Op tijdstip $t = 0$ bevindt de witte stip zich op het hoogste punt.

b

Schets de grafiek van $H$ voor ruim $2$ periodes.

c

Geef een formule voor $H (t)$ .

5

Los de onderstaande vergelijkingen algebraïsch op voor waarden van $t$ in het aangegeven interval. Geef je antwoorden afgerond op $3$ decimalen.
Controleer je antwoorden met je GR met intersect.

a

Voor $0 \leq t \leq 2 π$ : $\sin (2 t) = \frac{1}{4}$ .

b

Voor $0 \leq t \leq 2 π$ : $2 - 4 \cos (‐ t) = 5$ .

c

Voor $2 π \leq t \leq 6 π$ : $10 \sin (\frac{1}{2} t - 1) = ‐ 1$ .

d

Voor $2 π \leq t \leq 6 π$ : $\sqrt{2} \cos (π t - 5) = 2$ .

6

Hieronder staat de grafiek van een sinusoïde.

a

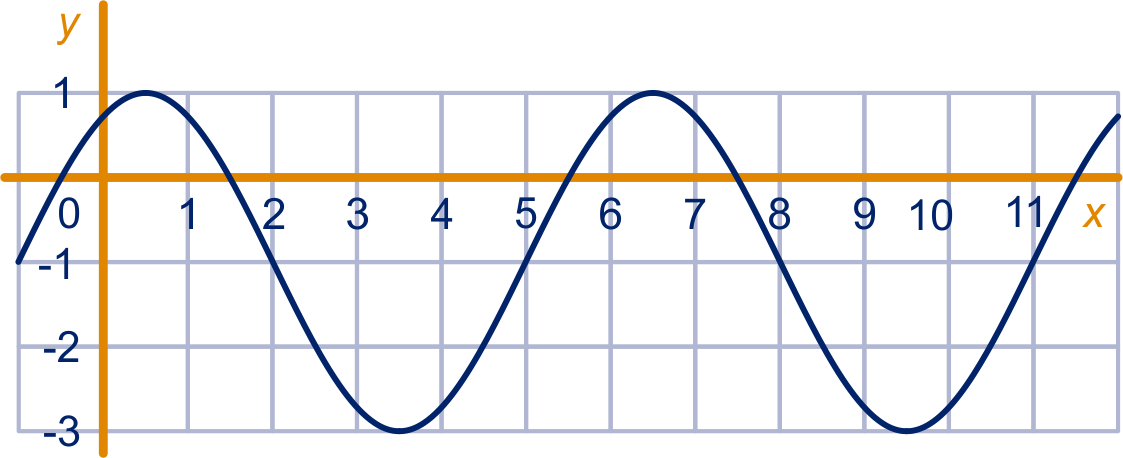
Geef (met toelichting) een formule bij de grafiek.

Deze sinusoïde wordt eerst met $2$ eenheden naar boven geschoven en daarna vermenigvuldigd met een factor $2$ ten opzichte van de $x$ -as.

b

Teken de nieuwe grafiek in het rooster op het werkblad.

c

Geef een formule voor de nieuwe sinusoïde.

d

Geef ook een formule voor de grafiek die je krijgt door de volgorde om te draaien, dus eerst ten opzichte van de $x$ -as te vermenigvuldigen en daarna omhoog te schuiven.