Gemiddelde groei

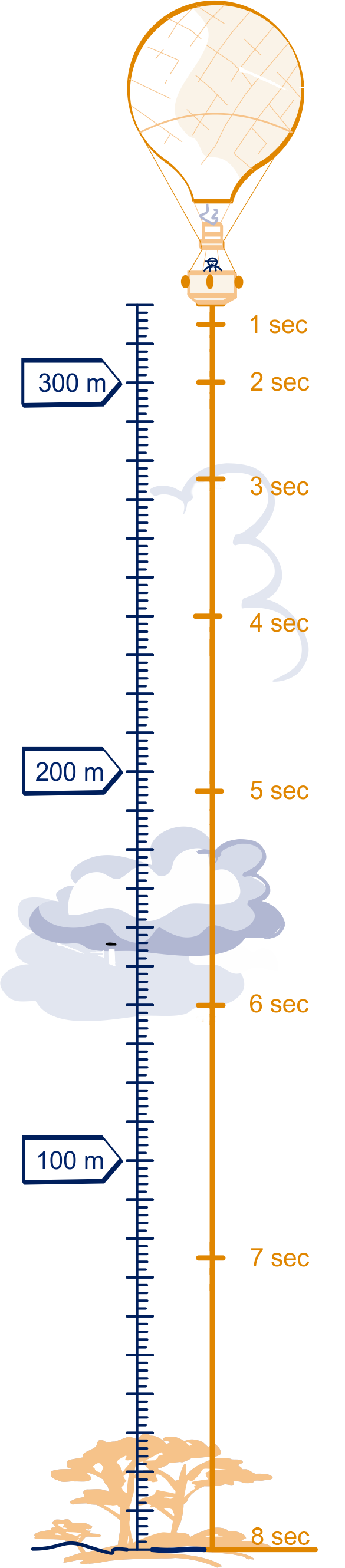
Uit een ballon op $320$ meter hoogte wordt een zandzakje geworpen. In de tekening hiernaast kun je zien waar het zakje zich na $1$ , $2$ , $3$ , $...$ , $8$ seconden bevindt. Je kunt de hoogte van het zakje boven de grond ook berekenen, namelijk met de formule $H = 320 - 5 t^{2}$ .

Controleer in de figuur of de formule klopt voor $t = 4$ en voor $t = 7$ .

Teken op de GR de grafiek van $H$ als functie van $t$ . Zet $t$ horizontaal uit en $H$ verticaal. Kies een geschikt window. Neem de figuur over.

Bereken de afstand die het zakje gemiddeld per seconde valt tussen de tijdstippen $t = 4$ en $t = 7$ .
Dat is de gemiddelde valsnelheid op het tijdsinterval $[4,7]$ .

Bereken ook de gemiddelde valsnelheid tijdens de laatste twee seconden van de val.

Opmerking:

Het woord interval komt uit het Latijn en betekent letterlijk tussenruimte. Het interval $[3,5]$ is de verzameling getallen tussen $3$ en $5$ , inclusief $3$ en $5$ zelf. De vierkante haken geven aan dat de getallen $3$ en $5$ zelf ook mee doen. Bij eenhoekige haken doen de randen niet mee. Bijvoorbeeld:
Tijdsinterval $[3,5]$ betekent alle waarden van $t$ waarvoor $3 \leq t \leq 5$ .
Tijdsinterval $〈 3,5 〉$ betekent alle waarden van $t$ waarvoor $3 < t < 5$ .

We gaan verder met de context van de vorige opgave.
Precies één seconde na het eerste zakje wordt een tweede zakje uit de ballon geworpen.

Teken in de figuur bij opgave 3b de grafiek van de hoogte van dit tweede zakje.

Hoeveel seconden later dan het eerste zakje bereikt het tweede zakje de grond?

Voor het tweede zakje geldt de formule: $H = 320 - 5 {(t - 1)}^{2}$ .

Controleer deze formule voor het begin- en eindtijdstip van zijn val.

Schrijf de formule voor het tweede zakje zonder haakjes en zo eenvoudig mogelijk.

Geef een formule voor het hoogteverschil tussen beide zakjes voor het tijdsinterval $[1,8]$ (dat wil zeggen voor de tijdstippen dat beide zakjes in de lucht zijn).

Teken de grafiek van dit hoogteverschil in de figuur bij opgave 3b.

Op een heldere dag in mei werd in De Bilt 's nachts om 05.00 uur de laagste temperatuur gemeten: $2 °$ C. Overdag liep de temperatuur snel op tot $18 °$ C. Dit maximum werd bereikt omstreeks 15.00 uur.

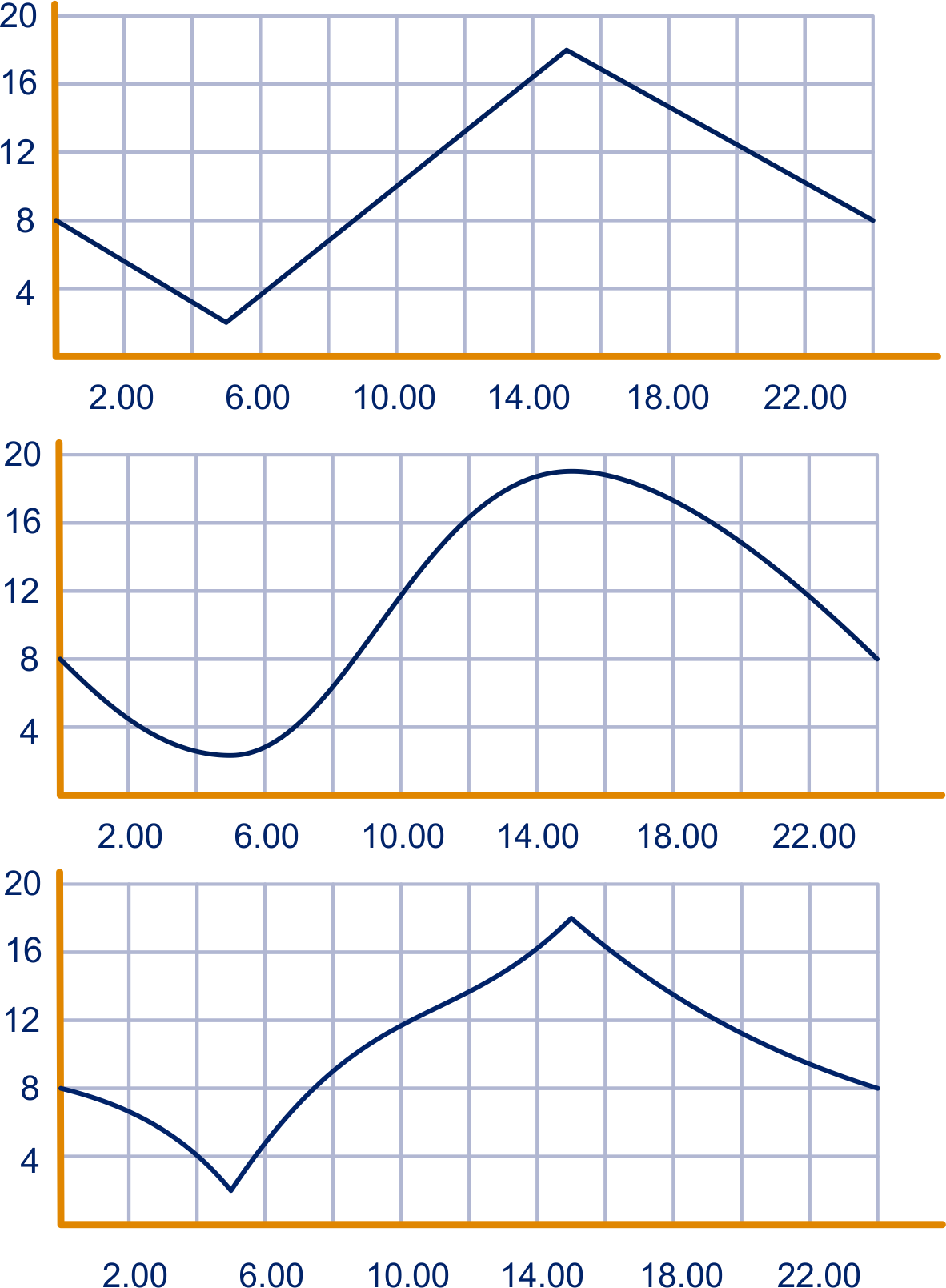
Hierboven staan drie grafieken.

Welke grafiek geeft volgens jou het beste het temperatuurverloop van die dag weer? Waarom?

De temperatuur $T$ (in $°$ C) is een functie van de tijd $t$ (in uren).

Bereken voor de grafiek die jij bij vraag a gekozen hebt de waarde van $\frac{Δ T}{Δ t}$ voor de periode van $5$ uur 's morgens tot $3$ uur 's middags.

Wat is de betekenis van de uitkomst van de vorige vraag?

Rond welk uur van de dag stijgt de temperatuur het snelst?

Hieronder is de groei van een zonnebloem in beeld gebracht.

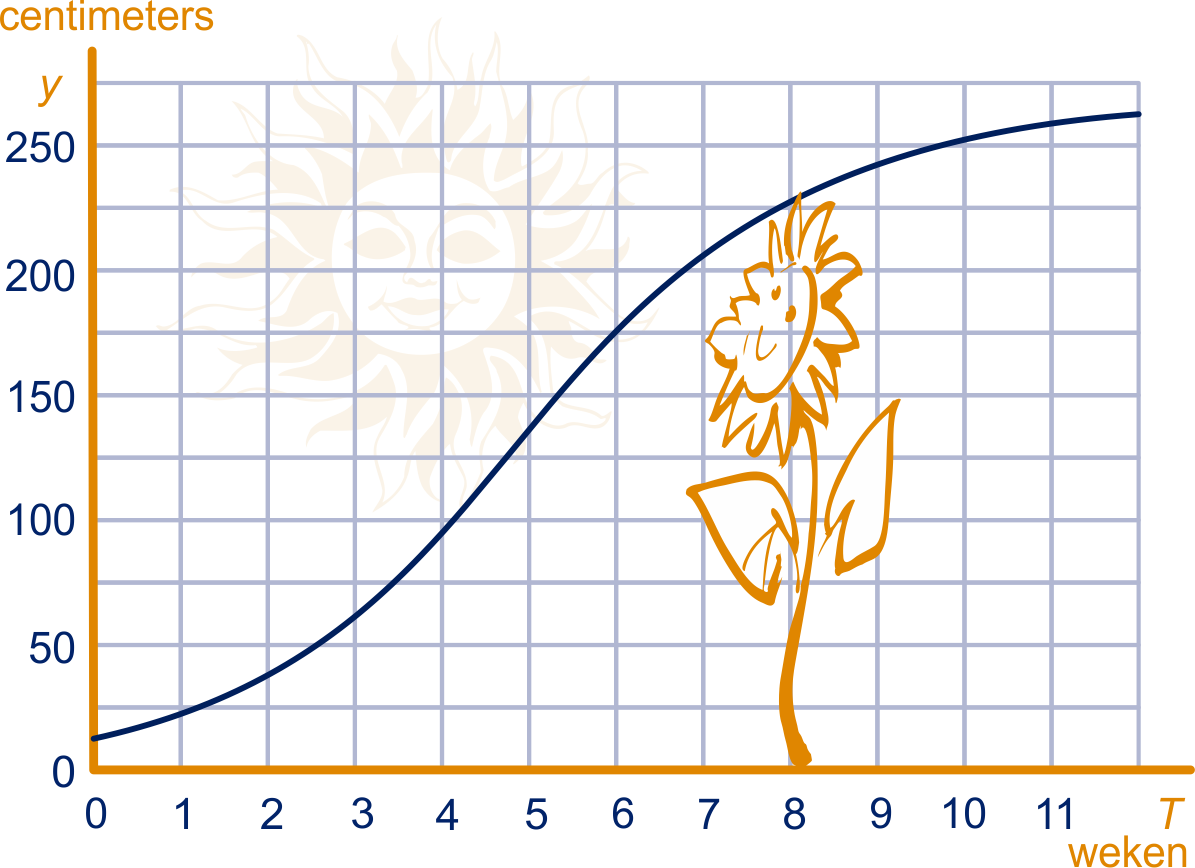
Hoeveel groeit de zonnebloem gemiddeld per week gedurende de vijfde tot en met de tiende week (dat zijn zes weken)?

In welke week groeit de zonnebloem het snelst?
Met hoeveel cm per dag?

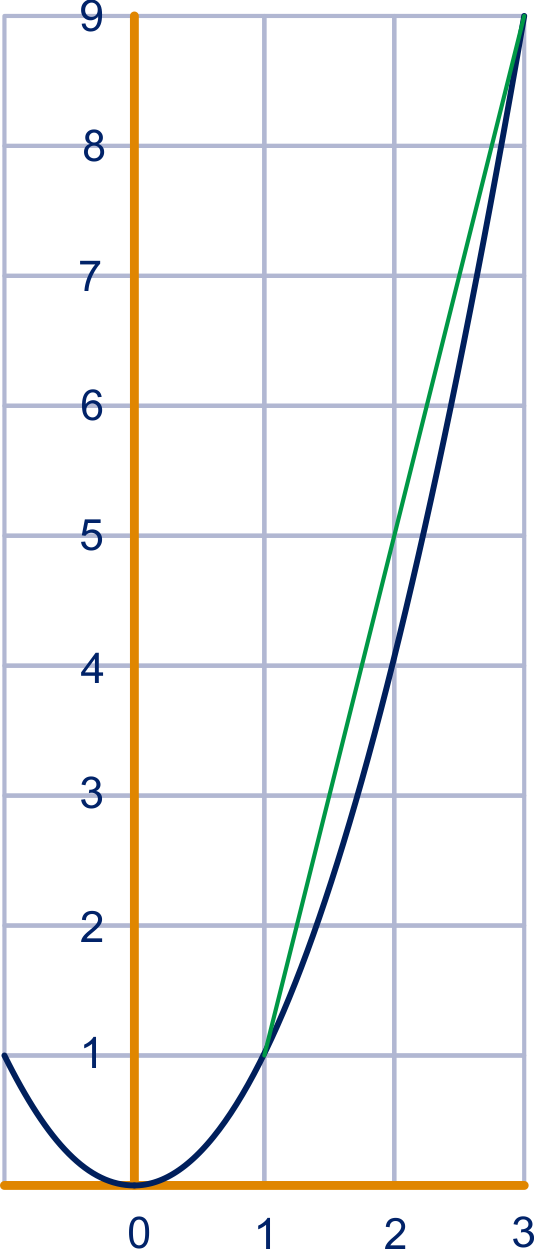
Hiernaast staat de grafiek van $y = x^{2}$ .
Als $x$ toeneemt van $1$ tot $3$ , dan neemt $y$ toe van $1$ tot $9$ .
De gemiddelde groei van $y$ is op het $x$ -interval $[1,3]$ dus gelijk aan $\frac{Δ y}{Δ x} = \frac{9 - 1}{3 - 1} = \frac{8}{2} = 4$ .

Bereken de gemiddelde groei van $y$ op de volgende $x$ -intervallen: $[3,6]$ , $[0,10]$ , $[‐ 2,2]$ en $[‐ 3,2]$ .

Bereken de gemiddelde groei van $y$ op het $x$ -interval $[a,3]$ .
Je krijgt een formule met $a$ erin. Vereenvoudig deze zover mogelijk.

Er is een getal $a$ (kleiner dan $3$ ) zo, dat de gemiddelde groei van $y$ op het $x$ -interval $[a,3]$ gelijk is aan $2$ .

Bereken dat getal $a$ .

Van een functie wordt de gemiddelde groei op het $x$ -interval $[a, b]$ berekend door het differentiequotiënt $\frac{Δ y}{Δ x}$ op dat interval uit te rekenen.
(Differentiequotiënt betekent letterlijk "uitkomst van deling van verschillen".)
Ofwel: de gemiddelde groei is gelijk aan de richtingscoëfficiënt van het verbindingslijnstuk tussen de twee punten op de grafiek bij $x = a$ en $x = b$ .

We bekijken nogmaals de functie $y = x^{2}$ .

Bereken de gemiddelde groei $\frac{Δ y}{Δ x}$ op het $x$ -interval $[2,009; 3,14]$ .

Wat is de toename $Δ y$ op het $x$ -interval $[a, b]$ ?

Wat is de toename $Δ x$ op het $x$ -interval $[a, b]$ ?

De gemiddelde toename op het $x$ -interval $[a, b]$ is dus
$\frac{Δ y}{Δ x} = \frac{b^{2} - a^{2}}{b - a}$ . Deze uitdrukking kun je vereenvoudigen.

Wat is die vereenvoudiging?

(hint)

Kijk nog eens naar de uitkomsten van opgave 7. Kun je een patroon ontdekken?

Waarschijnlijk heb je bij opgave 8d de volgende formule gevonden:
$\frac{b^{2} - a^{2}}{b - a} = b + a$ .
In de twee volgende opgaven gaan we deze formule bewijzen.

Voor alle getallen $a$ en $b$ , met $a \neq b$ , geldt: $\frac{b^{2} - a^{2}}{b - a} = b + a$ .

Waarom staat erbij dat $a \neq b$ ?

Controleer de juistheid van de formule voor de $x$ -intervallen $[3,6]$ en $[‐ 3,2]$ (zie opgave 7a).

Controleer de formule in het bijzondere geval dat $a = ‐ b$ .

Hoe luidt de formule in het bijzondere geval dat $a = 0$ ? Klopt dat?

Om de formule in het algemeen te bewijzen, schrijven we de teller van de formule eerst anders:
$b^{2} - a^{2} = (b - a) (b + a)$ .

Leg uit hoe de formule volgt uit onderstaande plaatjes.

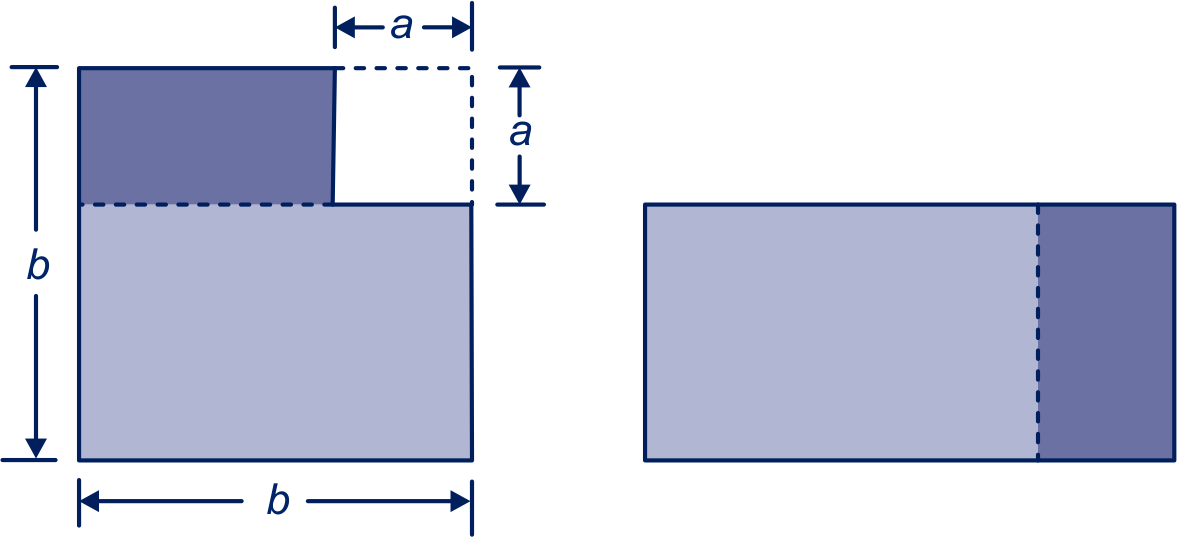
In deze plaatjes zijn $a$ en $b$ natuurlijk positieve getallen en $b$ is groter dan $a$ . Om te bewijzen dat de formule juist is voor alle getallen $a$ en $b$ moeten we anders te werk gaan.

Laat zien dat de formule juist is door de haakjes uit te werken in $(b - a) (b + a)$ .

Uit de voorgaande opgaven volgt het volgende.
De gemiddelde groei van $y = x^{2}$ op het $x$ -interval $[a, b]$ (met $a \neq b$ ) is $\frac{Δ y}{Δ x} = \frac{b^{2} - a^{2}}{b - a} = \frac{(b - a) (b + a)}{(b - a)} = b + a$ .

Geef (zonder veel rekenen) de gemiddelde groei van $y = x^{2}$ op de volgende $x$ -intervallen:
$[‐ 1,234; ‐ 1,766]$ , $[1 \frac{1}{6},1 \frac{5}{6}]$ en $[‐ 1,58; 2,58]$ .

Geef de gemiddelde groei van $y = x^{2}$ op de volgende $x$ -intervallen:
$[‐ p, p + 1]$ , $[p - \frac{1}{2}, p + \frac{1}{2}]$ en $[p, p + 2 \frac{1}{2}]$ .
(Hierin is $p$ een positief getal.)

Bereken de gemiddelde groei van $y = x^{2} + 5$ op de volgende $x$ -intervallen: $[1,3]$ , $[a,3]$ en $[a, b]$ .

Bereken de gemiddelde groei van $y = 3 x^{2}$ op dezelfde drie $x$ -intervallen.

Bereken de gemiddelde groei van $y = {(x - 1)}^{2}$ op dezelfde drie $x$ -intervallen.

Voor $y = x^{2}$ hebben wij het mooie resultaat dat de gemiddelde groei op het $x$ -interval $[a, b]$ gelijk is aan $a + b$ .
Bij andere functies zit er vooralsnog niets anders op dan de waarde van het differentiequotiënt $\frac{Δ y}{Δ x}$ uit te rekenen.

In deze opgave bekijken wij de functie $y = x^{2} + x$ .

Bereken het differentiequotiënt van de functie $y = x^{2} + x$ op de volgende $x$ -intervallen, vereenvoudig je antwoord zoveel mogelijk:
$[1,3]$ en $[2,5]$ .

Laat met een berekening zien dat het differentiequotiënt van de functie $y = x^{2} + x$ op het $x$ -interval $[a,3]$ gelijk is aan $a + 4$ .

(hint)

Bereken de breuk

\frac{Δ y}{Δ x}

en ontbind de teller in factoren.

Laat met een berekening zien dat op het $x$ -interval $[a, a + 1]$ geldt $\frac{Δ y}{Δ x} = 2 a + 2$ .

Laat met een berekening zien dat op het $x$ -interval $[a, b]$ geldt $\frac{Δ y}{Δ x} = b + a + 1$ .