geslacht, geboortejaar, geboortemaand, gewicht, lengte, gemiddeld cijfer over alle vakken, aantal uren huiswerk per week, wiskunde A of B, gekozen profiel, met plezier naar school
Bijvoorbeeld:
kwalitatief: geslacht, geboortemaand en profiel
kwantitatief: geboortejaar, gewicht en lengte
Nee, want er wordt geen hoeveelheid mee aangegeven.
Eenvoudig te meten, nauwkeuriger of onnauwkeuriger heeft weinig zin.
Linker weegschaal: analoog en continu, elke meetwaarde kan worden afgelezen.
Rechterweegschaal: digitaal en discreet, het weergegeven gewicht wordt afgerond (bijv. afgerond op gram, of op gram).
De gemiddelde maandtemperatuur geeft één meetwaarde per maand, dus verspringt van maand tot maand en tussenliggende waarden hebben geen betekenis.
geboortejaar: discreet, 1990 t/m 1994 (of 90 t/m 94)
gewicht: continu, (ongeveer) t/m kg
lengte: continu, (ongeveer) t/m cm
aantal talen: discreet, t/m
cijfer voor wiskunde (heel cijfer): discreet, t/m
cijfergemiddelde : continu, t/m
huiswerk (aantal uren per week): discreet, t/m
cm; cm
cm en cm komen beide keer voor.
-
Nummer .
-
Wouters gewicht is redelijk hoog; zijn cijfergemiddelde is laag t.o.v. de rest van de groep.
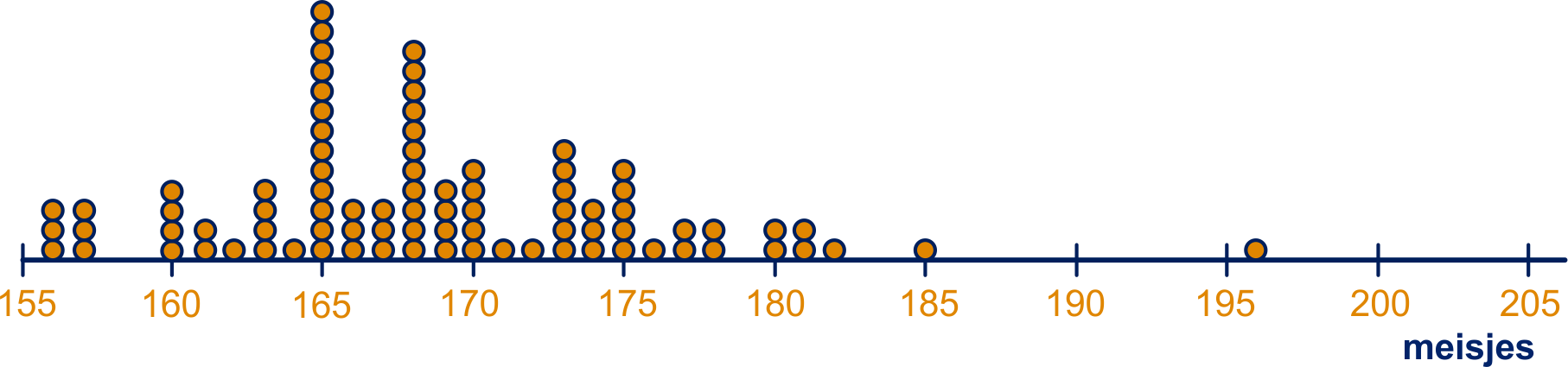
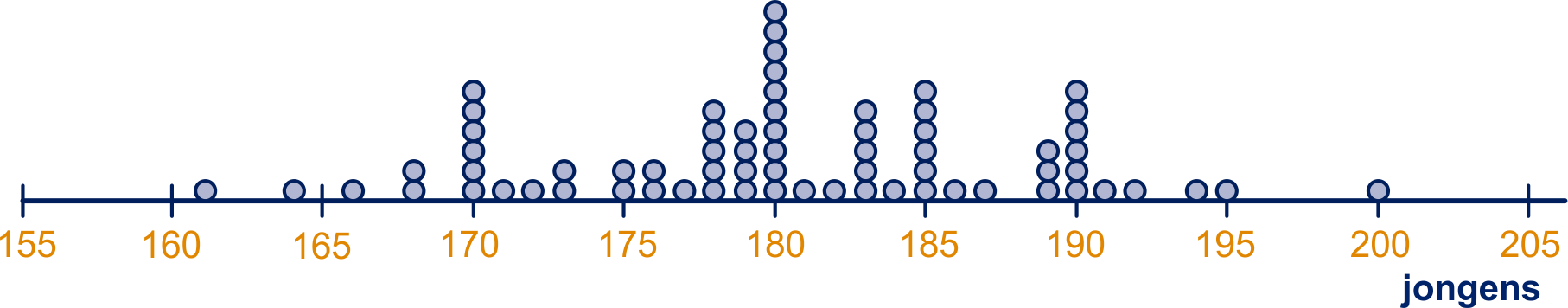
cm ;
cm ; cm
De meting van cm ligt erg ver van de rest af.
Voordeel: je kunt soms makkelijker in 1 oogopslag de waarden aflezen.
Nadeel: als steelgetal en bladgetallen niet makkelijk samen te stellen zijn, is een steelbladdiagram slecht te lezen.
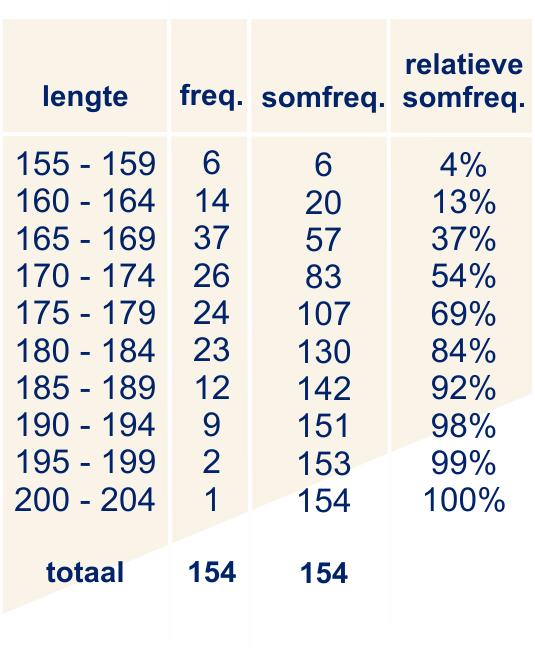
van de , dus ongeveer .
(Let op: maak klassenindeling met klasse van t/m ... etc., omdat anders de leerlingen met cm ook worden meegeteld.)
ja ; volgorde niet van belang
ja ; volgorde wel van belang
Omdat er maar jaren voorkomen.
ja ; volgorde wel van belang
De dagelijkse reistijd naar school: kwantitatief, continu, volgorde belangrijk, staafdiagram wel zinvol.
Het aantal lesuren per week: kwantitatief, discreet, volgorde belangrijk, staafdiagram wel zinvol.
De muziekvoorkeur: kwalitatief, volgorde niet belangrijk, staafdiagram wel zinvol.
Het belang van bewegingsonderwijs voor iedereen: kwalitatief, volgorde van belang, staafdiagram wel zinvol.
-
Wouters gewicht ( kg) is redelijk hoog; zijn cijfergemiddelde () zit ongeveer in het midden van de groep. In tegenstelling tot de dotplot weet je nu niet meer precies hoeveel anderen er meer wegen of een lager cijfer hebben.
De cijfers zijn omlaag gegaan.
De docent van H4C heeft dezelfde klassenbreedte gebruikt maar de klassengrenzen veranderd. De middelste klasse omvat nu alle leerlingen waarvan het cijfer ongeveer gelijk is gebleven.
-
-
, gebruik het histogram met een klassenbreedte van cm.
Nee, want cm bevindt zich in een klasse (bijvoorbeeld de klasse bij een klassenbreedte van cm) en je weet niet hoeveel leerlingen uit de klasse langer dan cm zijn.
Je krijgt een beter overzicht van de verdeling van de lengtes.
De ruwe data is niet meer zichtbaar en alleen schattingen voor waarden in klassen zijn nog mogelijk.
Je krijgt steeds minder klassen en verliest daardoor nog meer van de precieze gegevens.
klassenbreedte ; klassenmiddens ; enz.
klassenbreedte ; klassenmiddens ; ; enz.
klassenbreedte ; klassenmidden
Lengte, gewicht, gemiddelde cijfer, huiswerk. Dit zijn kwantitatieve variabelen met een redelijke spreiding.
-
Je ziet meteen dat Wouters gewicht redelijk hoog is en zijn cijfergemiddelde laag t.o.v. de rest van de groep.
Bij een somfrequentiepolygoon staan de stippen altijd boven de rechter grens van een klasse: je leest immers af hoeveel mensen een lengte hebben tot en met het einde van een klasse. Dat is dus anders dan bij een gewoon frequentiepolygoon. Daar staan de stippen boven de klassenmiddens. De eerste stip staat boven de linker grens van de eerste klasse aangezien alle waarnemingen boven de linker grens van de kleinste klasse zitten.
-
-
;
tussen en cm ; tussen en cm
tussen en cm ; tussen en cm
De derde: de meeste bolletjes zitten links, dus aan de linkerkant moeten de sommen telkens flink stijgen, terwijl de sommen aan de rechter kant heel weinig zullen stijgen (weinig bolletjes).
Ja, met moeite; nee, niet direct (beide antwoorden zijn correct).
Nee, je weet immers niet hoe de aantallen binnen een klasse zijn verdeeld.
Beschrijving schetsje aan de hand van de eerste klasse: in plaats van één klasse () krijg je vijf klassen tussen en en ieder van de vijf klassen heeft dezelfde frequentie, nl. . Je verdeelt de tien waarnemingen tussen en dus evenredig over de vijf klassen: je weet niet hoe de waarnemingen in werkelijkheid waren verdeeld over deze vijf klassen (als je alleen dit staafdiagram met klassen van seconde hebt) en daarom ziet dit schetsje er anders uit dan de dotplot.
In de diagrammen met klassenindelingen - zoals het histogram - kun je makkelijker direct zien wat de meest gesprinte tijden waren. In de dotplot moet je daar meer moeite voor doen. De klassenindeling werkt als een samenvatting en dat maakt het makkelijker om de meest gesprinte tijden snel af te lezen.
Een somfrequentiepolygoon.
