9.3 Vermenigvuldigen en delen (1) >

Hoofdstukken > Getallenlijn

We hebben geleerd hoe we gehele getallen moeten optellen en aftrekken, nu willen we natuurlijk ook gaan vermenigvuldigen en delen.

Je weet dat $3 \cdot 5$ betekent $5 + 5 + 5$ . Evenzo geldt dat $3 \cdot ‐5 = ‐5 + ‐5 + ‐5$ .
Zo kunnen we een stuk van de tafel van $‐5$ opschrijven.
$1 \cdot ‐5 = ‐5$
$2 \cdot ‐5 = ‐10$
$3 \cdot ‐5$
$4 \cdot ‐5$
$5 \cdot ‐5$

Neem de tafel van $‐5$ van hierboven over en vul hem verder in.

Neem de tafel van $‐7$ over en vul hem verder in.
$1 \cdot ‐7$
$2 \cdot ‐7$
$3 \cdot ‐7$
$4 \cdot ‐7$
$5 \cdot ‐7$

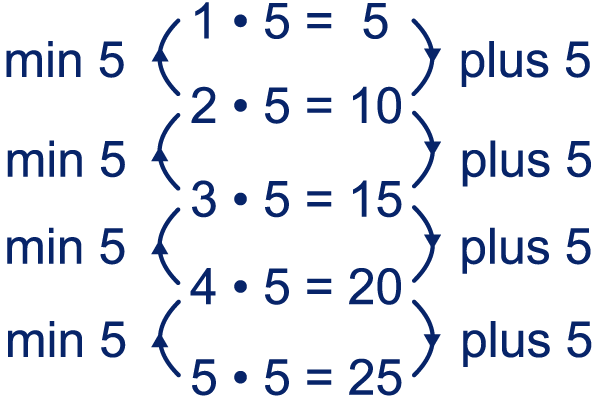
We bekijken eens goed het begin van de tafel van 5: elke keer als je een stapje omlaag gaat, komt er 5 bij. Zo kun je bijvoorbeeld $6 \cdot 5$ berekenen:
$6 \cdot 5 = 25 + 5 = 30$ , want $6 \cdot 5$ staat één stapje onder $5 \cdot 5$ .

Elke keer als je een stapje omhoog gaat, gaat er 5 vanaf. Die regelmaat willen we voortzetten en zo gaan we $0 \cdot 5$ , $‐1 \cdot 5$ , $‐2 \cdot 5$ , enzovoorts uitrekenen.

$0 \cdot 5$ staat één stapje boven $1 \cdot 5$ .
Wat moet er volgens die regelmaat uit $0 \cdot 5$ komen?

Vul de uitgebreide tafel van 5 verder in.
Werk van onder naar boven.

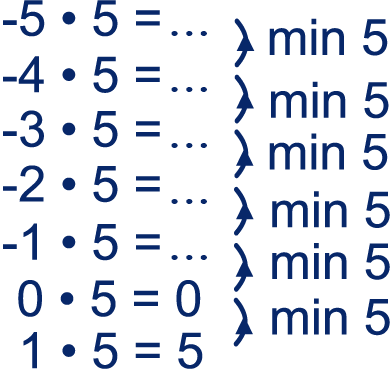
Maak ook de uitgebreide tafel van $‐7$ .
Werk weer van onder naar boven.

Bereken (lukt het niet uit je hoofd, schrijf dan een stukje van de uitgebreide tafel op):

$3 \cdot ‐8$	$‐2 \cdot 4$
$‐3 \cdot ‐6$	$5 \cdot ‐9$
$‐7 \cdot 1$	$‐5 \cdot ‐5$
$7 \cdot ‐7$	$‐9 \cdot 2$
$‐8 \cdot ‐9$	$‐5 \cdot 0$

Bij de deling $10 : 2 = 5$ hoort de vermenigvuldiging $2 \cdot 5 = 10$ . Als je tien knikkers met z'n tweeën moet delen, krijgt iedereen er 5, want $2 \cdot 5 = 10$ .
Neem over en vul in.
$‐10 : 2 = .....$ , want $2 \cdot ..... = ‐10$
$10 : ‐2 = .....$ , want .....
$‐10 : ‐2 = .....$ , want .....
$21 : ‐7 = .....$ , want .....
$‐72 : ‐9 = .....$ , want .....
$‐48 : 12 = .....$ , want .....

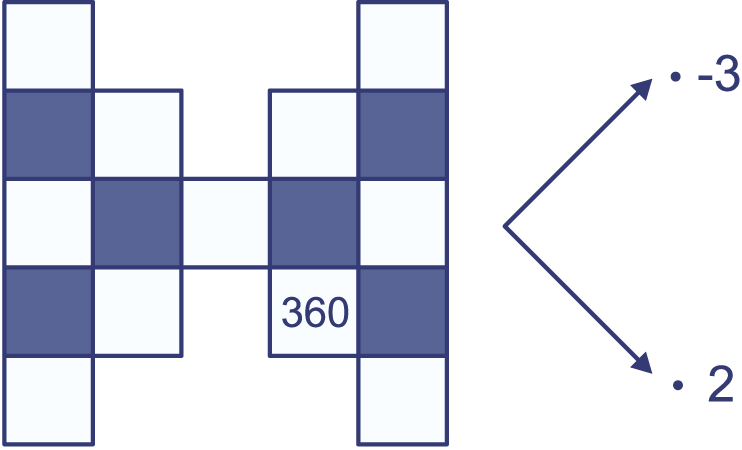
Elke keer dat je in noordoostelijke richting gaat in de figuur vermenigvuldig je met $‐3$ . Elke keer dat je in zuidoostelijke richting gaat vermenigvuldig je met 2.

Neem de figuur over en vul de lege vakjes in.

Als het goed is heb je in de middelste rij de getallen $‐30$ , 180 en $‐1080$ gevonden.
Je ziet dat $‐1080$ ten oosten staat van 180 en $‐30$ ten westen van 180.

Als je de figuur zou uitbreiden, welk getal zal dan ten oosten van $‐1080$ staan?

En welk getal ten westen van $‐30$ ?

Als je twee positieve getallen vermenigvuldigt is de uitkomst positief.
Als je een positief getal vermenigvuldigt met een negatief getal is de uitkomst negatief.
Als je een negatief getal vermenigvuldigt met een positief getal is de uitkomst negatief.
Als je twee negatieve getallen vermenigvuldigt is de uitkomst positief.

Schrijf zo eenvoudig mogelijk; de eerste is als voorbeeld al gemaakt:

$‐3 \cdot ‐ a = 3 a$	$2 \cdot 6 a \cdot a$
$‐1 \cdot a$	$‐ a \cdot 6 \cdot ‐2$
$‐ b \cdot ‐ b$	$b \cdot 7 \cdot ‐ b$
$‐3 \cdot a \cdot ‐1$	$‐2 \cdot ‐2 a \cdot ‐2$

Rekenen met haakjes

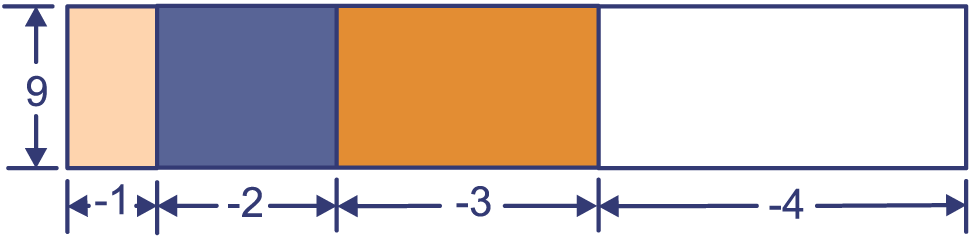
Van de rechthoek is de lengte 3 en de breedte $x + 2$ .

Schrijf de oppervlakte van de rechthoek op twee manieren.
manier 1:
$totale oppervlakte = oppervlakte donkere deel + oppervlakte witte
deel$
manier 2:
$totale oppervlakte = lengte \cdot breedte$

Welke gelijkheid kun je nu opschrijven?

Als we $‐5 (x - 4)$ zonder haakjes willen schrijven, kunnen we een zelfde plaatje gebruiken. We weten dat $‐5 (x - 4) = ‐5 (x + ‐4)$ . De rechthoek heeft dus een "lengte" van $‐5$ en een "breedte" van $x + ‐4$ .

Welke gelijkheid kun je nu opschrijven?

De gelijkheden $a (b + c) = a b + a c$ en $a (b - c) = a b - a c$
zijn juist voor alle gehele getallen $a$ , $b$ en $c$ .

Bereken de volgende sommen. Schrijf ook een tussenstap op. De eerste som is als voorbeeld al gemaakt.

$‐13 \cdot ‐25 + ‐13 \cdot ‐75 = ‐13 \cdot ‐100 = 1300$

$50 \cdot 32 + 50 \cdot ‐62$
$125 \cdot ‐23 + 75 \cdot ‐23$
$‐26 \cdot ‐18 + 126 \cdot ‐18$
$‐37 \cdot ‐58 + 37 \cdot ‐58$

Bereken ( $x$ is een variabele):
$‐1 \cdot 9 + ‐2 \cdot 9 + - 3 \cdot 9 + ‐4 \cdot 9 = ..... \cdot 9 = .....$
$‐1 \cdot ‐7 + ‐2 \cdot ‐7 + ‐3 \cdot ‐7 + ‐4 \cdot ‐7$
$‐1 \cdot x + ‐2 \cdot x + ‐3 \cdot x + ‐4 \cdot x$

Schrijf zonder haakjes en zo eenvoudig mogelijk. De eerste opgave is als voorbeeld al gemaakt ( $x$ en $y$ zijn variabelen).
$‐3 (x - 5) = ‐3 x + 15$
$‐6 (‐4 + x)$
$‐5 (‐3 - y)$
$x (‐1 - y)$
$x (7 + ‐7)$

10s

Neem de opgaven over en vul de lege plekken in.
$..... (3 x - .....) = 12 x - 6$
$..... (4 x + 6) = ‐8 x - .....$
$‐ \frac{1}{2} (.....) = ‐ x + 5$
$..... (..... - 6 x) = ‐18 + 9 x$

Waar of niet waar? Neem de foute gelijkheden over en verbeter ze.

$x + ‐ x = 0$	$x - ‐ x = 0$
$x - 0 = ‐ x$	$0 - x = ‐ x$
$1 \cdot x = x$	$0 \cdot x = x$
$‐1 \cdot x = ‐ x$	$‐1 \cdot ‐ x = ‐ x$

Opmerking:

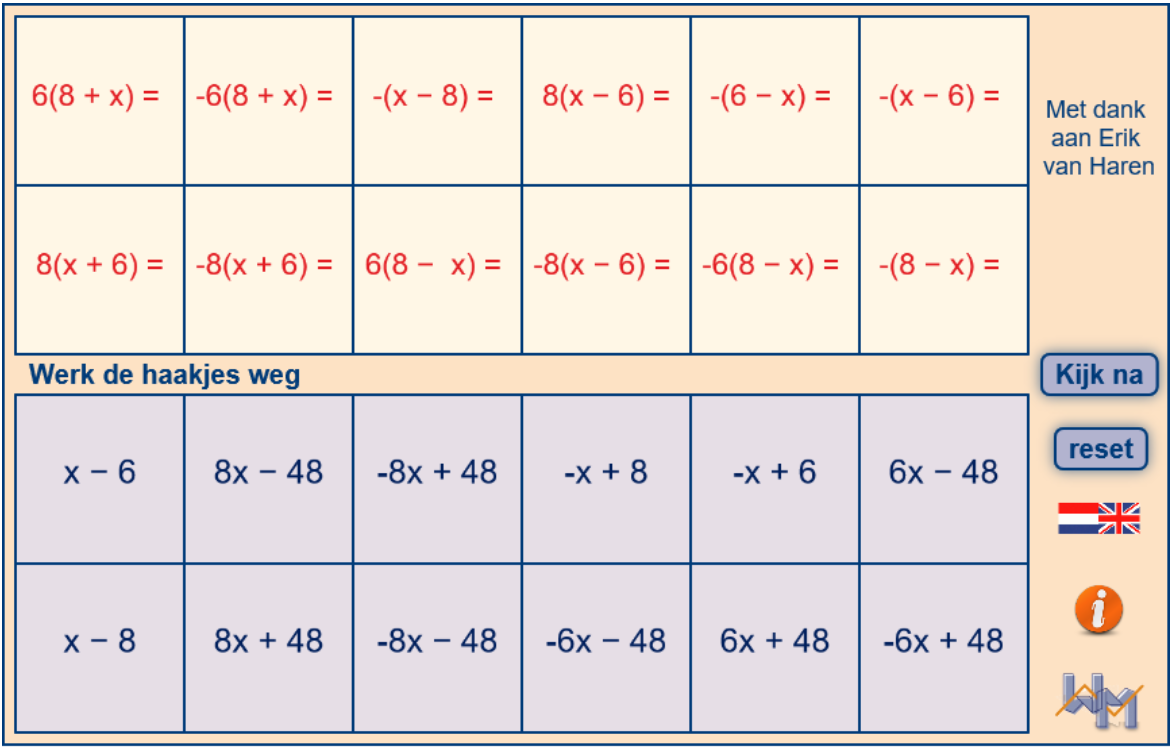
Om het rekenen met negatieve getallen in combinatie met formules met haakjes nog extra (spelenderwijs) te oefenen, tot je het snel en foutloos doet, kun je meerdere keren de volgende mini-loco maken.
Distributiewet, met negatieve getallen .