160 – 77 = 83 of 160 – 78 + 1 = 83 bladzijdes heeft Jan gelezen.
98 – 22 = 76 of 98 – 23 + 1 = 76 bladzijdes heeft Marie gelezen.
De 1ste bladzijde heeft nummer 45. De 37ste bladzijde is 36 bladzijdes verder, dus 45 + 36 = 81 is het nummer van zijn laatste bladzijde.
Voor Bart staan de personen met de nummers 27 t/m 54. Dat zijn 54 – 26 = 28 personen.
De 71ste bladzijde heeft nummer 210. De 1ste bladzijde is 70 bladzijdes terug, dus op bladzijde 210 – 70 = 140 begon Anne vandaag te lezen.
Van de 28ste naar de 1ste is 27 edities terug, dus 2023 – 27 = 1996, dus in het jaar 1996.
foldernummer is en het lotnummer is
nummer van de folder is ;
huisnummer is
of of of of ...
zaal: ; balkon:
of
euro
KB KD KP BD BP DP
6
4
De eerste en de derde keer.
wandelingen ; wandelingen ; wandelingen
jjj jjn jnj jnn njj njn nnj nnn, er zijn er 8.
Van naar gaat over de eerste vraag, van naar over de tweede vraag enzovoort. Bovenlangs gaan is ja, onderlangs nee.
7×6 = 42 of 7×7–7 = 42 wedstrijden worden er in totaal gespeeld.
12×11 = 132 of 12×12–12 = 132, dus uit 12 teams.
De competitie bestond uit 10 teams, want 10×9 = 90. Dus elk team moest (10–1)×2 = 18 wedstrijden spelen.
8×7:2 = 56:2 = 28 wedstrijden worden er in totaal gespeeld. (of 1+2+3+4+5+6+7 = 28)
11×10:2 = 55, dus uit 11 teams. (In een hele competitie zouden er 55×2 = 110 wedstrijden gespeeld worden, en dat is 11×10, dus uit 11 teams.)
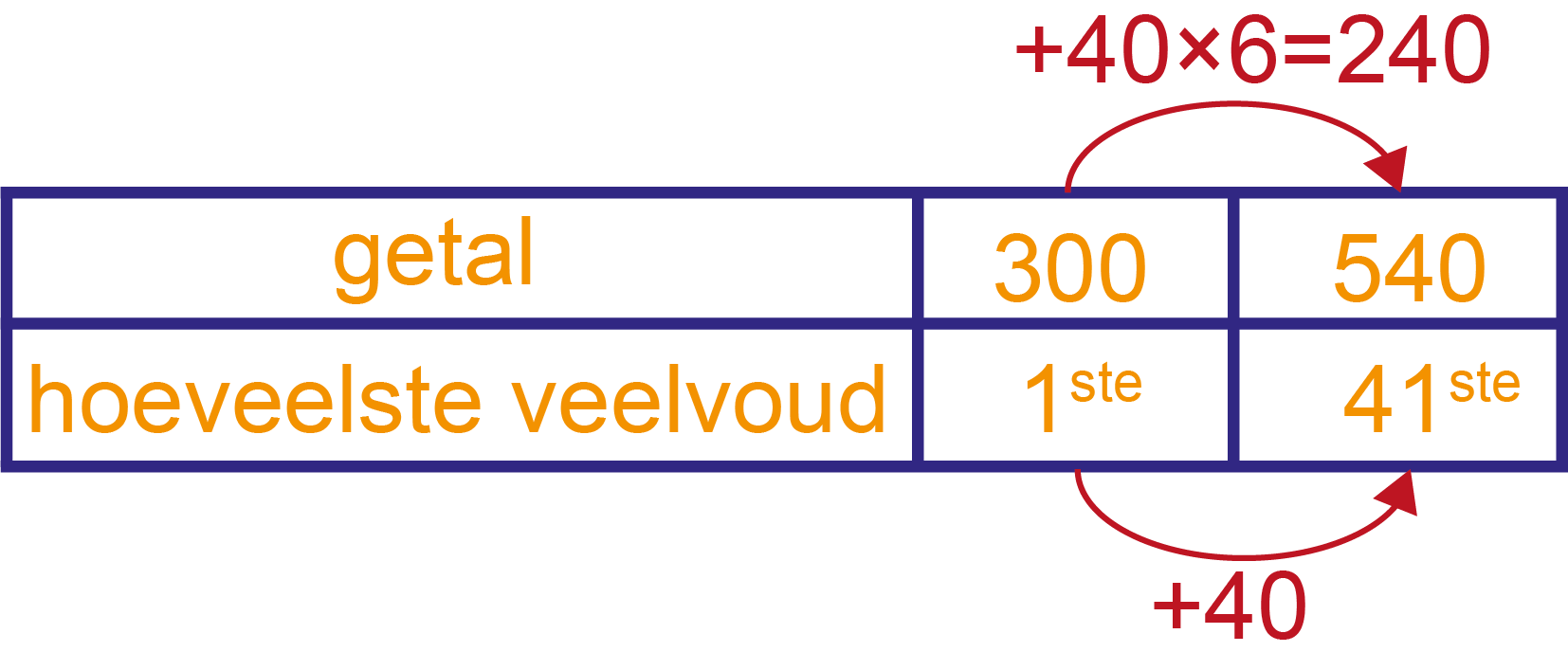
Het 1ste veelvoud is 300. Het 41ste is 40 veelvouden van 6 verder, dus
300 + 40×6 = 300 + 240 = 540 is het 41ste veelvoud. Zie ook tabel.
De 1ste veelvoud is 306, de 2de 312. De laatste veelvoud van 6 is het getal 912, dat is 600 meer dan het getal 312, dat zijn dus 100 veelvouden van 6 meer dan de 2de veelvoud van 312. Dus in totaal 102 veelvouden. Zie ook tabel.
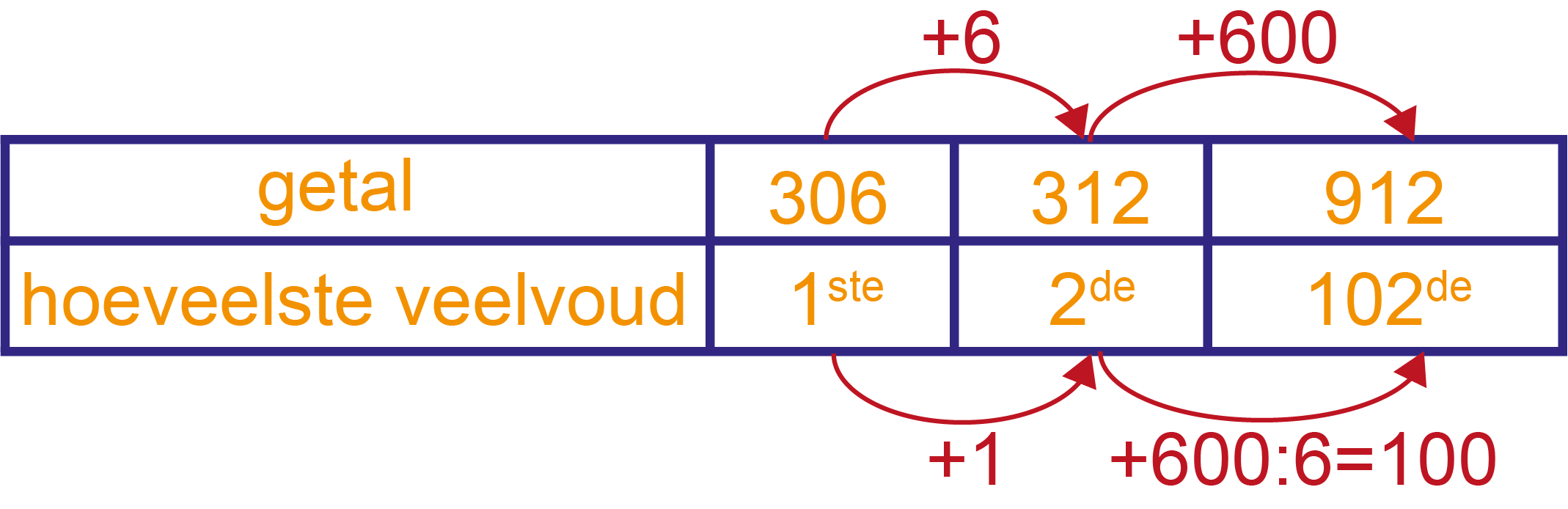
Dat zijn er 203. Zie tabel.
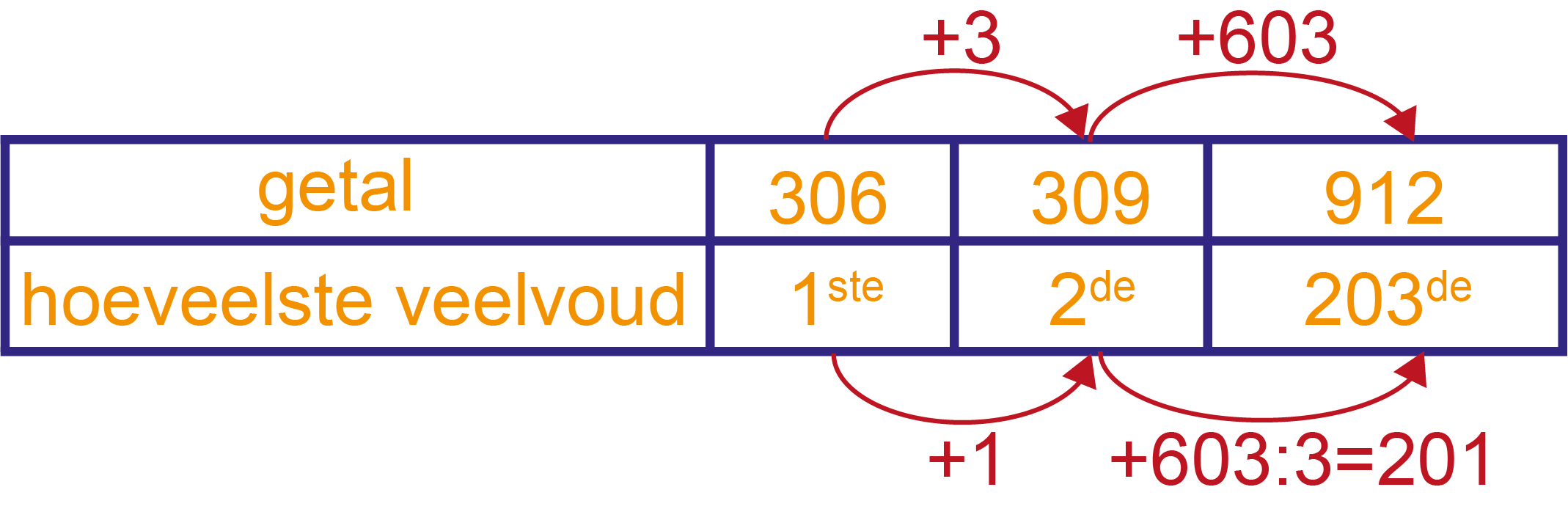
Dat was in het jaar 2022 – 27×4 = 1914 in Chamonix.
Dat was in het jaar 1928 – 8×4 = 1896.
(2020 – 1896):4 + 1 = 32ste zomerspelen in Japan.
40; 40; 9; 6
Het kleinste getal is het KGV van de getallen en vermeerderd met .
Dus .
nee; nee; ja; nee; nee; ja
Dat zijn de getallen , ,... tot en met . Dat zijn even veel getallen als het aantal getallen van 0 tot en met 100, dus 101.
Als het getal bestaande uit de twee laatste cijfers deelbaar is door 4 dan is het getal zelf deelbaar door 4 en omgekeerd. Want het verschil van die twee getallen is een veelvoud van 100 en dat is deelbaar door 4.
Je moet naar de laatste drie cijfers kijken.
Op manieren.
1 bij 1 op manieren, 3 bij 3 op manieren, 4 bij 4 op manieren, enzovoort.
7
27
pinnen: 5 ; ringen:
99 kleiner
9 kleiner
Omdat wat het kleiner wordt ook deelbaar is door 9.
Niet, omdat wat het kleiner wordt wel deelbaar is door 9.
Omdat wat het kleiner wordt ook deelbaar is door 9 en dus ook deelbaar is door 3.
deelbaar door 9: ja; ja; nee; ja; ja
Natuurlijk geldt voor de deelbaarheid door 3 hetzelfde.
De opdracht van Harrie zorgt ervoor dat je altijd een veelvoud van 9 krijgt en bij de veelvouden van 9 staat dezelfde kat.